腐烂的苹果
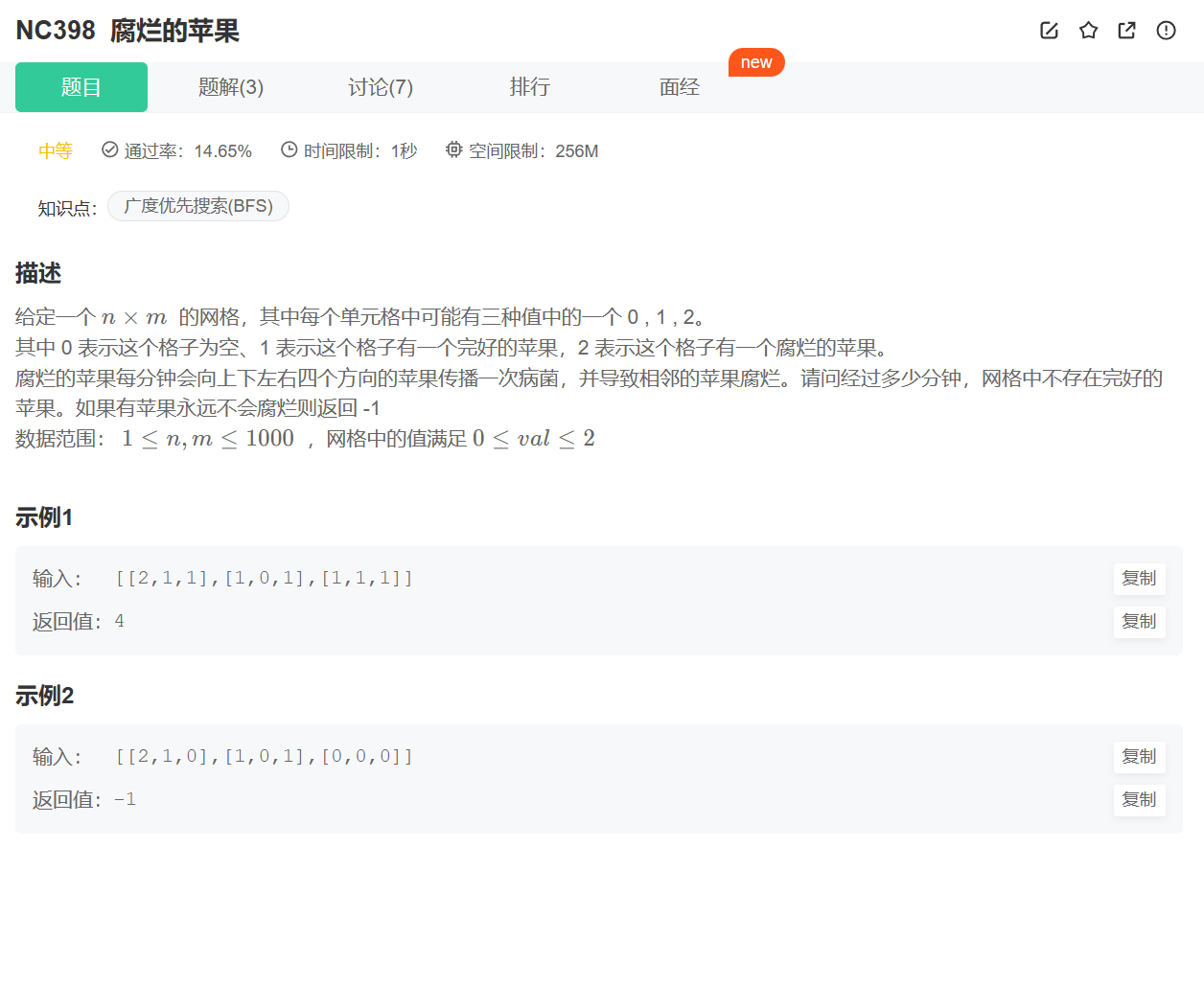
一个腐烂的苹果每分钟可以向上下左右四个方向扩展,扩展之后,又会有新的腐烂的苹果,一直去腐蚀好的苹果,求多少分钟后,网格中全是烂苹果。
第一次做这道题的时候,想到这道题考察的其实是多源BFS的知识点了。
多源BFS
把所有的源点当成一个超级源点。问题就变成了单一的单源最短路问题
将所有腐烂的苹果全部放到一个队列里面,然后层层的向外扩展,每次扩展都要把队列里面所有的烂苹果给pop出去。bfs搜索会把一个烂苹果周围的好苹果放入到队列里面,因为每分钟烂苹果都要向外扩展一次,所以队列里面的烂苹果向外扩展耗费的时间是同一分钟。
class Solution {
public:
int n, m;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
queue<pair<int, int>> q;
int rotApple(vector<vector<int> >& g) {
// write code here
n = g.size();
m = g[0].size();
// 将所有烂苹果当成一个大的烂苹果
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j++) {
if (g[i][j] == 2) {
q.push({i, j});
}
}
}
// 记录耗费的时间
int ret = 0;
while (!q.empty()) {
// 每次扩展都要将队列清空
int sz = q.size();
ret++;
while (sz--) {
auto [i, j] = q.front();
q.pop();
for (int t = 0; t < 4; t++) {
int x = i + dx[t];
int y = j + dy[t];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 1) {
// 遍历过的苹果不能在遍历到了,可以搞一个bool数组,也可以在原数组上进行修改
g[x][y] = 2;
// 好苹果加入到队列当中
q.push({x, y});
}
}
}
}
// 判断是否有苹果不能被腐蚀
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (g[i][j] == 1)
return -1;
return ret - 1;
}
};