今天我们来学习一个新的专题,「快速幂」技巧。
斐波那契数列 相信大家都不陌生,小学的找规律题目中就经常见到它的身影。
递推表达式为:
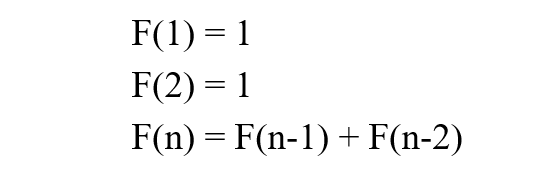
根据该表达式,可以很轻松的写出递归版本的代码:
public static int f(int n) {
if (n < 1) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
return f(n - 1) + f(n - 2);
}
该递归代码非常容易理解,这里不做过多讲解。相信小伙伴们也都知道其存在的问题:包含了大量的重复计算!
接下来就引出我们今天要介绍的 「矩阵快速幂」 技巧。
注意:以下内容需要用到 线性代数 中的 矩阵乘积 运算哦~
关系推导
我们将 两个相邻项 写成矩阵形式,由此可以得到如下关系式:
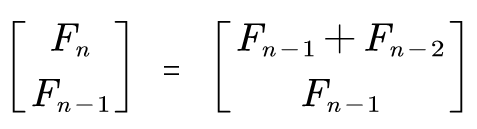
将右侧通过 矩阵乘积 提出 系数矩阵 后得到:
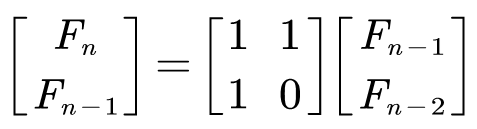
(这是不是就变成了数列的递推式了)
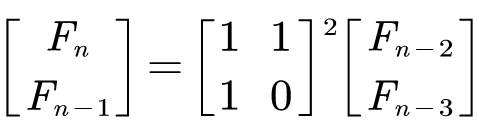

我们惊讶的发现,最终要求的 F n Fn Fn 只和系数矩阵的 n − 2 n-2 n−2 次幂以及数列的前两项的值(已知)有关。
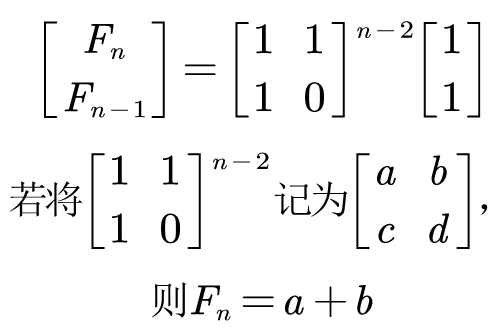
推导到这里,我们关注的焦点就聚焦在了如何快速求出某个 矩阵的高次幂 。
在介绍 矩阵高次幂 前,我们先来回顾一下 幂运算:
数的高次幂
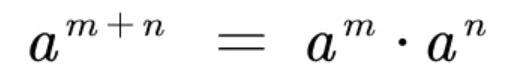
这个公式对于计算高次幂来说有何启发呢?
计算机对于二进制的计算非常方便快捷,因此我们就想到,如果我们将高次幂的计算划归成与二进制有关的计算是不是就方便很多了呢~
下面我们通过一个例子进行说明:
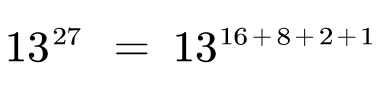
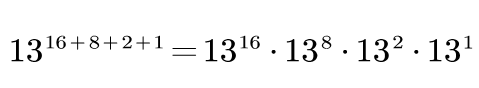
分解后,对于每一项的计算都变得很简单了,只需要底数 13 依次与自己相乘,就能按照 1、2、4、8、16…的指数增长了。计算答案只需将指数 27 的二进制中含有 1 的项乘入结果中,最终就能完成计算。时间复杂度仅为 O ( l o g N ) O(logN) O(logN)(如果直接底数一遍一遍的相乘复杂度为 O ( N ) O(N) O(N))。
public static long fastPower(long base, long p) {
long res = 1;
// 指数不为 0 就一直循环,指数右移一位
for (; p != 0; p >>= 1) {
// 只有当前末位为 1 时,结果res中乘入此时的底数base
if ((p & 1) != 0) {
res *= base;
}
// 底数依次与自己相乘,得到 1、2、4、8、16 次方
base *= base;
}
return res;
}
矩阵高次幂
在了解了数字高次幂的计算方法后,矩阵的高次幂怎么计算,想必小伙伴们也都有思路了。对应过来就行啦~
注意: 数字里的 1 ,在矩阵中为 单位矩阵E 。

直接看代码:
private static int[][] matrixPower(int[][] m, int p) {
int[][] res = new int[m.length][m[0].length];
// 构造单位矩阵 E
for (int i = 0; i < res.length; i++) {
res[i][i] = 1;
}
int[][] t = m;
// 与计算数的高次幂方法一致
for (; p != 0; p >>= 1) {
if ((p & 1) != 0) {
res = produce(res, t);
}
t = produce(t, t);
}
// 返回计算出的高次幂矩阵
return res;
}
// 计算两个矩阵相乘的结果矩阵
private static int[][] produce(int[][] a, int[][] b) {
int n = a.length;
int m = b[0].length;
int k = a[0].length;
int[][] ans = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
for (int c = 0; c < k; c++) {
ans[i][j] += a[i][c] * b[c][j];
}
}
}
return ans;
}
到这里,我们就解决了矩阵的高次幂问题。
回归主线,对于解决斐波那契数列的第 N 项来说,在得到系数矩阵的 n − 2 n-2 n−2 次方后即可计算出来。
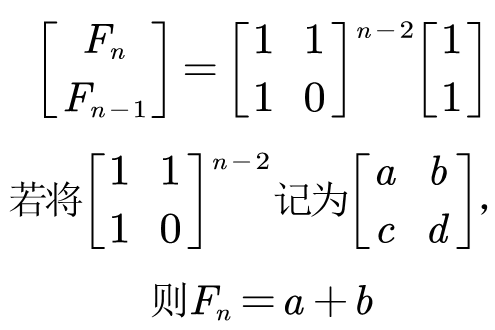
快速幂求解斐波那契代码
public static int f(int n) {
if (n < 1) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
int[][] base = { { 1, 1 }, { 1, 0 } };
// 计算系数矩阵的高次幂
int[][] res = matrixPower(base, n - 2);
// res中 00 和 01 位置求和,即 a+b
return res[0][0] + res[0][1];
}
当求解一个较大的斐波那契数
F
(
46
)
F(46)
F(46) 时,两种不同算法的执行时间对比也很明显:
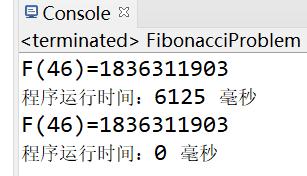
本题结合了线性代数的知识,可能稍微有点儿难度,小伙伴们认真体会思想哦~
学完整个思路我们发现:其实最关键的是 系数矩阵的求解 。本题的系数矩阵是通过递推公式得到的。
换一道题目,不同的递推公式就会对应不同的系数矩阵哦!接下来的几篇文章我们继续加深对于 系数矩阵的求解方法 。
~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
关注回复「ACM紫书」获取 ACM 算法书籍~