深度学习过程中,若模型出现了过拟合问题体现为高方差。有两种解决方法:
- 增加训练样本的数量
- 采用正则化技术
增加训练样本的数量是一种非常可靠的方法,但有时候你没办法获得足够多的训练数据或者获取数据的成本很高,这时候正则化技术就可以有效的帮助你避免模型过拟合。接下来本文就来讲解一下深度学习中的正则化起作用的原理(文中以L2正则化为例)。
有关正则化的基础知识,可以回看我之前的文章哦:
【机器学习300问】18、正则化是如何解决过拟合问题的?![]() http://t.csdnimg.cn/vX2mP
http://t.csdnimg.cn/vX2mP
一、包括L2正则化项的损失函数长什么样
在损失函数(如均方误差、交叉熵误差等)的基础上,L2正则化引入了一个与权重向量W相关的正则化项,通常表示为:
| 符号 | 解释 |
| 包含正则化项的总损失函数 | |
| 代表未加正则化项的原始损失函数,这通常是对每个样本的损失的平均值,如交叉熵损失或均方误差损失 | |
| 分别表示网络中的权重和偏置参数 | |
| 正则化项的系数,这是一个超参数,用于控制正则化的强度 | |
| 训练样本的数量 | |
| L2正则化项,通常称为权重衰减项。是所有权重矩阵的Frobenius范数的平方的和。Frobenius范数是一个矩阵范数,等同于矩阵元素的平方和的平方根 | |
表示第 |
二、L2正则化的作用机制
(1)权重缩小
在优化过程中,由于L2正则化项的存在,当模型试图降低原始损失时,同时需要考虑减小权重的平方和。这会促使模型在训练过程中选择较小的权重值,避免权重值过大导致模型对训练数据的过度敏感。
(2)防止过拟合
较小的权重值意味着模型对单个特征的影响不会过于突出,减少了模型对训练数据中噪声和个别样本特性的过度学习,有利于提高模型在未见过数据上的泛化能力。
三、L2正则化到底是怎么起作用的嘛!
(1)微观上,对激活函数的影响
激活函数tanh(双曲正切函数)的输出范围在-1到1之间,形状类似于Sigmoid函数但更为平缓,且在两端饱和区的梯度更接近于0。公式就不赘述了之前的文章详细介绍过了,我们在这里只关注函数的图像,从图像上理解就可以了。

用表示,那么我们发现,只要
非常小,如果
只涉及少量参数,我们就只利用了双曲正切函数的线性状态,如下图所示:

当L2正则化惩罚过大时,模型的权重被迫保持较小的值,也就是说也会很小。对于tanh激活函数意味着:
- tanh函数接近线性(斜率为1),较小的权重导致输入信号大部分位于tanh函数的线性区域内,使得模型的非线性表达能力减弱,趋向于线性模型。
- 过强的L2正则化可能会限制tanh激活函数充分发挥其非线性变换的能力,尤其是对于需要捕捉复杂非线性关系的任务,模型可能无法有效学习数据的深层次结构。
在之前的文章中讲到过,如果激活函数都是线性函数,那么无论你的神经网络有多深,节点有很多,都相当于一个简单的线性模型。这就是为什么L2正则化通过约束权重的大小,间接降低了模型的复杂度。
(2)宏观上,对神经网络结构的影响
现在我们假设一种很极端的情况,正则化参数非常大,因此对权重的惩罚非常大,导致权重很小,小到约等于0。因为公式
,我们如果不考虑偏置。就会得到
,这样一来从神经网络的在该节点的输出
。意味着这个神经元死亡了。如果用图来表示的话就是:
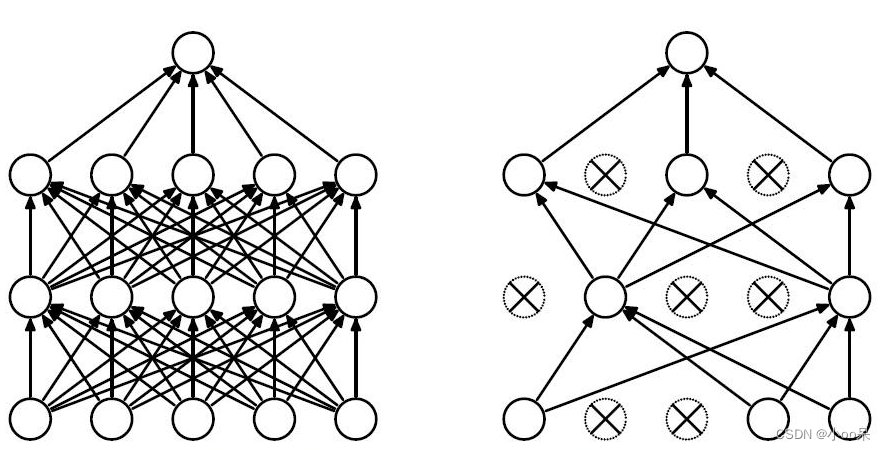
显然,模型的复杂度被降低了,提高模型的泛化能力。