C++ 散列表（hash table）

news2024/9/29 9:19:13

目录

一，哈希表

1，哈希表概述

2，哈希函数

3，碰撞冲突

二，代码实现

1，哈希函数与素数函数

2，哈希节点与哈希表数据结构

3，构造、析构以及一些简单的功能

4，清空，扩容 

5，查找，插入，删除

三，完整代码

一，哈希表

1，哈希表概述

散列表（也称为哈希表（hash table））是一种通过哈希函数来计算数据存储位置的数据结构，使得对数据的插入、删除和查找操作可以非常快速进行。哈希表可以说是一种专门用来查找的数据结构。在最理想的情况下，哈希表的这些操作的时间复杂度为O(1)。那么，它是怎么做到如此高效的呢？

我们先来考虑一下这个：如果我们要查找的键都是小整数，我们可以用一个数组来实现无序的符号表，将键作为数组的索引而数组中下标 i 处储存的就是它对应的值。这样我们就可以快速访问任意键的值。

哈希表就是这种简易方法的扩展，它能够处理更加复杂的类型的键，使用哈希查找算法分为两步。

  1.  第一步是用哈希函数将被查找的键转化为一个哈希值（数组的一个索引）。理想情况下，不同的键都能转化为不同的哈希值。不过实际上我们需要面对多个键都会散列到相同的哈希值的情况。因此我们就需要进行第二步。
  2. 哈希查找的第二步就是去处理哈希值的碰撞冲突，碰撞冲突是不可避免的。

发生碰撞的示意图：

2，哈希函数

使用哈希算法的第一步就是哈希函数的计算，这个过程会将键转化为哈希值。如果我们有一个能够保存 m 个键值对的数组，那么我们就需要一个能够将任意键转化为该数组范围内的索引 [0, m-1] 范围内的整数的散列函数。哈希函数和键的类型有关。严格地说，对于每种类型的键都我们都需要一个与之对应的哈希函数。

我们来看下面几个例子：

Ⅰ 正整数

将整数散列最常用方法是除留余数法。我们选择大小为素数 m 的数组对于任意正整数 k，计算 k % m 就能得到数组的索引。这个函数的计算非常容易并能够有效地将键散布在 [0, m-1] 的范围内。

这里为什么要用素数呢？选择一个素数 m 作为数组的大小有助于减少哈希冲突的可能性。这是因为当使用除留余数法计算索引时，如果 m 是一个非素数，那么某些位置更容易被选中（例如输入的数据恰好是 m 的倍数），这样会增加发生碰撞冲突的可能性。

所以我们在为底层的数组容器分配空间时最好分配素数大小的空间。（不过后文为了方便实现就没有采用这个方式）

Ⅱ 字符串

除留余数法也可以处理较长的键，例如字符串，我们只需要将字符串转为一个正整数之后再用除留余数法就可以了：

size_t k = 0;

// 这一步的处理是为了将字符串转换成正整数的分布更散
int seed = 131;
for (char ch : str) {
	k *= seed;
	k += ch;
}

size_t idx = k % m;

Ⅲ 结构体

如果键的类型含有多个整型变量，我们可以和 string 类型一样将它们混合起来。例如，
假设被查找的键的类型是日期类型 Date，我们可以这样计算它的散列值:

struct Data {
	int day;
	int month;
	int year;
};

size_t k = ((day * 131 + month) * 131 + year);
size_t idx = k % m;

要为一个数据类型设计一个优秀的哈希函数需要满足三个条件：

① 一致性：相同的键必须得到相同的哈希值

② 高效性：计算简单

③ 均匀性：均匀的散列说有的键

不过设计专门的哈希函数就是专家们的事情了。

3，碰撞冲突

哈希算法的第二步是碰撞处理，也就是处理多个键的哈希值相同的情况。解决碰撞问题的方法有很多种，例如：线性探测，二次探测，开链法等等，这些方法会在不同的情况下有着不同的效率。

Ⅰ线性探测

当哈希计算出某个元素的插入位置，而该位置上的空间已不再可用时，最简单的处理办法就是循序往下一一寻找(如果到达尾端，就绕到头部继续寻找)，直到找到一个可用空间为止。只要数组足够大就肯定能够找到一个空间，但是要花多少时间就很难说了。

进行元素查找操作时，道理也相同，如果哈希函数计算出来的位置上的元素值与我们的搜寻目标不符，就循序往下一一寻找，直到找到吻合者，或直到遇上空格元素。

至于元素的删除，必须采用惰性删除，也就是只标记删除记号，实际删除操作则等底层数组重新开辟空间时再进行。这是因为使用线性探测法的哈希表中的每个元素不仅表述它自己，也关系到其它元素的排列。

Ⅱ 二次探测

二次探测与线性探测十分相似，仅仅只是搜寻新空间的方式不同：如果哈希函数计算出新元素的位置为 idx，而该位置实际上已被使用，那么我们就依序尝试 idx + 1^2，idx + 2^2，idx + 3^2，idx + 4^2  …  idx + n^2，而不是像线性探测那样依序尝试 idx + 1，idx + 2，idx + 3，idx + 4  ….  idx + n。

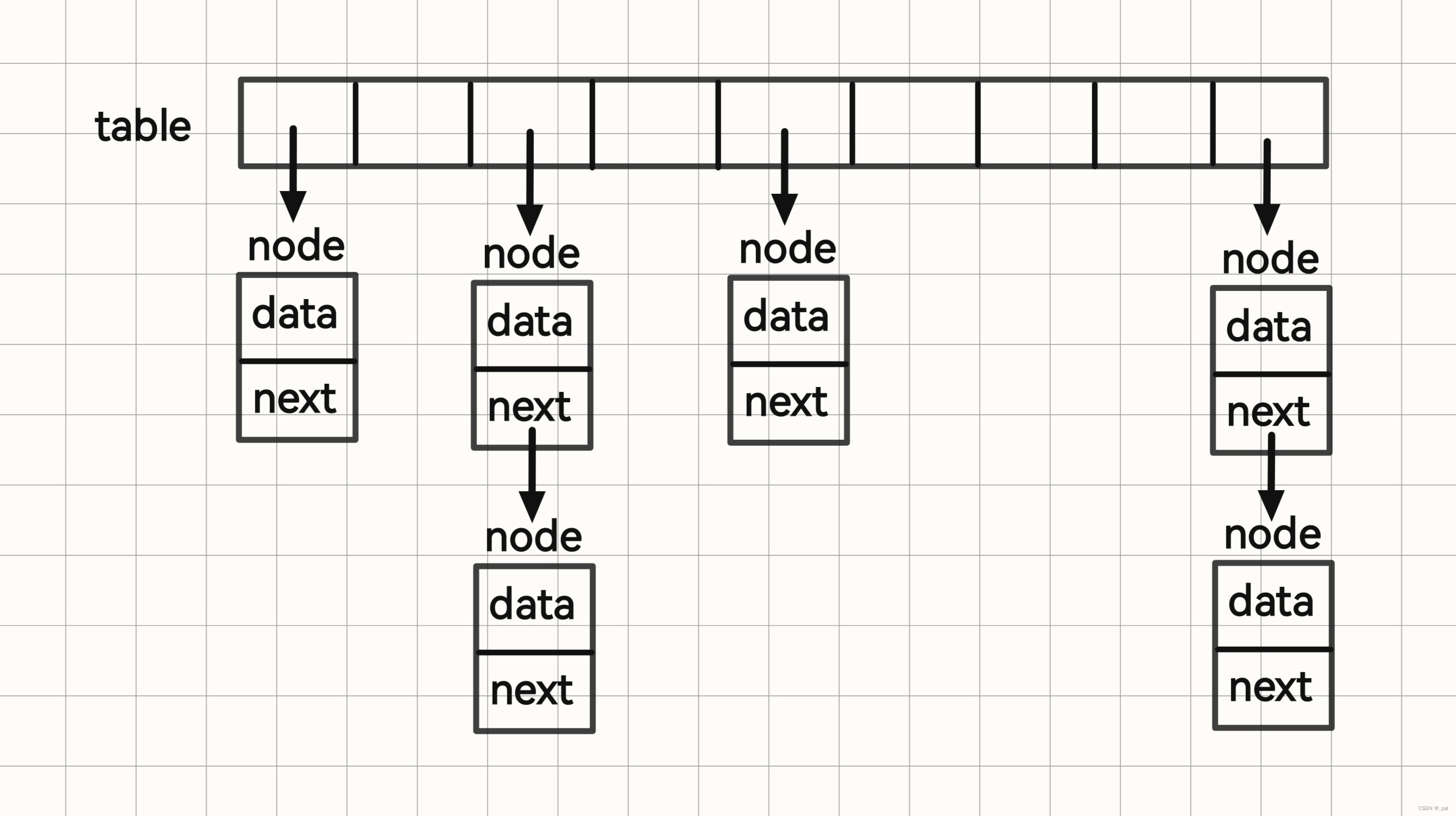
Ⅲ 开链法

这种办法是将大小为 m 的数组中的每个元素都指向一条链表，链表中的每个结点都存储了散列值为该元素的索引的值。发生冲突的元素都被存储在链表中。这个方法的基本思想就是选择足够大的m ，使得所有链表都尽可能短以保证高效的查找。这种查找方式分为两步：① 根据哈希值找到对应的链表；② 沿着链表顺序查找相应的键。（在后文中实现的哈希表将基于开链法来实现）

开链法示意图：

二，代码实现

1，哈希函数与素数函数

首先是哈希函数

// 这里的哈希函数只是将数据类型转换为正整数, 将正整数转换为数组索引的工作交给哈希表内部去完成
// 哈希函数族
template<class Key>
struct hash_func {
	size_t operator()(const Key& key)const {
		return key;
	}
};
template<>
struct hash_func<std::string> {
	// 将字符串转换为数字
	size_t operator()(const std::string& str)const {
		size_t res = 0;
		int seed = 131;
		for (char ch : str) {
			res *= seed;
			res += ch;
		}
		return res;
	}
};

因为我们在对底层的 vector 扩容时选择素数大小可以减少发生碰撞冲突的可能，所以这里提供了一些关于素数的函数（我们也可以提前将素数列表给罗列出来，这样就不用进行查找）：

// 寻找并返回不小于 n 的最小素数的函数
size_t prime(int n) {
	// 检查一个数是否为素数的函数
	std::function<bool(int)> is_prime = [](int num) {
		if (num <= 1) return false;  // 处理非正整数
		if (num <= 3) return true;   // 2 和 3 是素数
		if (num % 2 == 0 or num % 3 == 0) return false; // 排除能被 2 或 3 整除的数
		for (int i = 5; i * i <= num; i += 6) {
			if (num % i == 0 or num % (i + 2) == 0) return false;
		}
		return true;
	};

	if (n <= 2) return 2;			// 特殊处理小于等于 2 的情况
	if ((n & 1) == 0) n++;			// 如果 n 是偶数，从下一个奇数开始检查
	while (not is_prime(n)) n += 2;	// 只检查奇数

	return n;
}

2，哈希节点与哈希表数据结构

template<class T>
struct hash_node {
	T data;
	hash_node* next;
	hash_node(const T& _data = T()) :data(_data), next(nullptr) {}
};
template<class Key, class HashFunc = hash_func<Key>>
class hash_table {
	// ...
private:
	typedef hash_node<Key> Node;
	HashFunc _hf;

private:
	size_t _size;
	std::vector<Node*> _table;
	// ...
};

3，构造、析构以及一些简单的功能

public:
	// 构造与析构
	hash_table() :_size(0), _table(11, nullptr) {}	// 默认预留11个空间
	~hash_table() { if (not empty()) clear(); }

public:
	// 一些简单的功能
	bool empty()const { return _size == 0; }
	size_t size()const { return _size; }
	size_t table_size()const { return _table.size(); }

	void swap(hash_table& ht) {
		std::swap(_size, ht._size);
		_table.swap(ht._table);
	}

	// 为了便于扩展，这里将 prime 函数在 hash_table 内部再封装一层
	size_t next_size(size_t size)const { return prime(size); }
	// 为了方便找到索引而设计的函数
	size_t table_index(const Key& key)const { return _hf(key) % table_size(); }
	size_t table_index(const Key& key, size_t table_size)const { return _hf(key) % table_size; }

4，清空，扩容 

因为 hash_table 中底层容器 vector 中存放的是单向链表，所以我们在进行清空，扩容操作时需要特别注意内存的开辟与释放问题。

public:
	// 清空
	void clear() {
		for (int i = 0;i < _table.size();++i) {
			Node* node = _table[i];
			while (node) {
				Node* next = node->next;
				delete node;
				node = next;
			}
			_table[i] = nullptr;
		}
		_size = 0;
		
	}

	// 扩容 table
	void resize(size_t size) {
		size = next_size(size);
		if (size <= _size) return;
		std::vector<Node*> newTable(size, nullptr);
		for (Node* node : _table) {
			while (node) {
				// int idx = _hf(node->data) % newTable.size();
				int idx = table_index(node->data, newTable.size());
				Node* next = node->next;
				node->next = newTable[idx];
				newTable[idx] = node;
				node = next;
			}
		}
		// _table = std::move(newTable);
		_table.swap(newTable);
		
	}

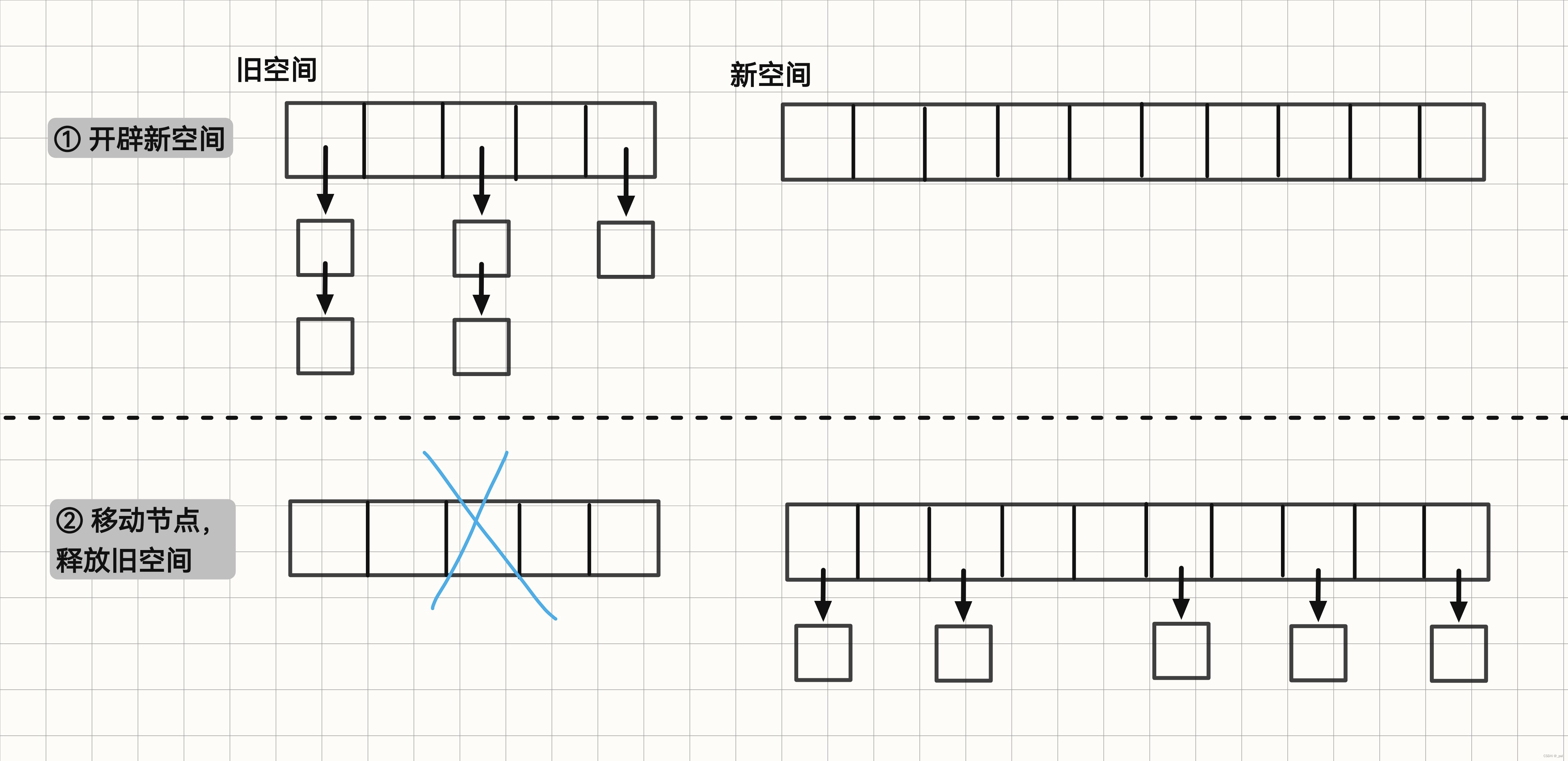
这里特别说明一下 resize 操作的步骤：

① 新开辟一个 vector 来当作存放哈希节点的新空间

② 将原 vector 中的所有节点通过 table_index 函数重新计算索引后移动到新的 vector 中（注意，这里并不是拷贝，而是移动）

③ 将新的 vector 作为新的底层容器

扩容示意图：

5，查找，插入，删除

hash table 的查找十分高效，不过 hash table 中存放的元素并不是有序的，如果我们想按照范围来查找数据，我们因该选择 AVL 或者红黑树来当作我们的容器。

public:
	Node* find(const Key& key)const {
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		for (Node* node = _table[idx];node;node = node->next) {
			if (node->data == key) return node;
		}
		return nullptr;
	}

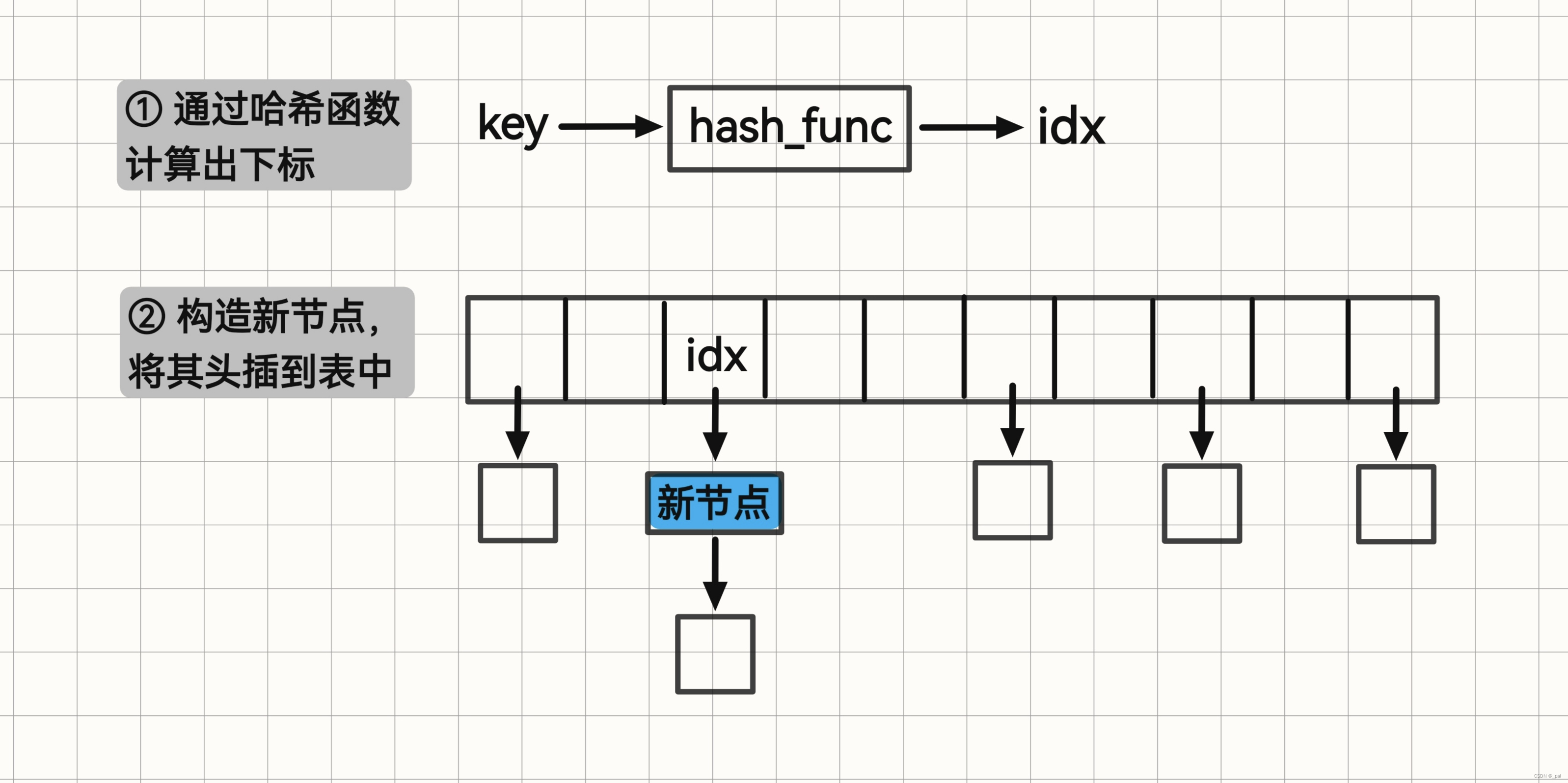
	pair<Node*, bool> insert(const Key& key) {
		if (_size == _table.size()) {
			//扩容table
			resize(_size * 2);
		}
		// 取得下标
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		if (_table[idx] == nullptr) {
			_table[idx] = new Node(key);
		}
		else {
			for (Node* node = _table[idx];node != nullptr;node = node->next) {
				// key已经存在就直接返回
				if (node->data == key) return make_pair(node, false);
			}
			Node* node = new Node(key);
			// 头插
			node->next = _table[idx];
			_table[idx] = node;
		}
		++_size;
		return make_pair(_table[idx], true);
	}


	void erase(const Key& key) {
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		Node* dummy = new Node;
		dummy->next = _table[idx];
		Node* pre = dummy, * cur = dummy->next;
		while (cur) {
			if (cur->data == key) {
				pre->next = cur->next;
				_table[idx] = dummy->next;
				delete cur;
				--_size;
				break;
			}
			pre = cur;
			cur = cur->next;
		}
		delete dummy;
	}

因为右值引用版的插入与左值引用版的插入代码基本一致，这里就不详细实现了。

插入示意图：

三，完整代码

template<class T>
struct hash_node {
	T data;
	hash_node* next;
	hash_node(const T& _data = T()) :data(_data), next(nullptr) {}
};


// 这里的哈希函数只是将数据类型转换为正整数, 将正整数转换为数组索引的工作交给哈希表内部去完成
// 哈希函数族
template<class Key>
struct hash_func {
	size_t operator()(const Key& key)const {
		return key;
	}
};
template<>
struct hash_func<std::string> {
	// 将字符串转换为数字
	size_t operator()(const std::string& str)const {
		size_t res = 0;
		int seed = 131;
		for (char ch : str) {
			res *= seed;
			res += ch;
		}
		return res;
	}
};



// 寻找并返回不小于 n 的最小素数的函数
size_t prime(int n) {
	// 检查一个数是否为素数的函数
	std::function<bool(int)> is_prime = [](int num) {
		if (num <= 1) return false;  // 处理非正整数
		if (num <= 3) return true;   // 2和3是素数
		if (num % 2 == 0 || num % 3 == 0) return false; // 排除能被2或3整除的数
		for (int i = 5; i * i <= num; i += 6) {
			if (num % i == 0 || num % (i + 2) == 0) return false;
		}
		return true;
	};

	if (n <= 2) return 2;			// 特殊处理小于等于2的情况
	if ((n & 1) == 0) n++;			// 如果n是偶数，从下一个奇数开始检查
	while (not is_prime(n)) n += 2;	// 只检查奇数
	return n;
}



template<class Key, class HashFunc = hash_func<Key>>
class hash_table {
private:
	typedef hash_node<Key> Node;
	HashFunc _hf;

private:
	size_t _size;
	std::vector<Node*> _table;

public:
	// 构造与析构
	hash_table() :_size(0), _table(11, nullptr) {}	// 默认预留11个空间
	~hash_table() { if (not empty()) clear(); }

public:
	// 一些简单的功能
	bool empty()const { return _size == 0; }
	size_t size()const { return _size; }
	size_t table_size()const { return _table.size(); }

	void swap(hash_table& ht) {
		std::swap(_size, ht._size);
		_table.swap(ht._table);
	}

	// 为了便于扩展，这里将 prime 函数在 hash_table 内部再封装一层
	size_t next_size(size_t size)const { return prime(size); }
	// 为了方便找到索引而设计的函数
	size_t table_index(const Key& key)const { return _hf(key) % table_size(); }
	size_t table_index(const Key& key, size_t table_size)const { return _hf(key) % table_size; }

public:
	// 清空
	void clear() {
		for (int i = 0;i < _table.size();++i) {
			Node* node = _table[i];
			while (node) {
				Node* next = node->next;
				delete node;
				node = next;
			}
			_table[i] = nullptr;
		}
		_size = 0;
		
	}

	// 扩容 table
	void resize(size_t size) {
		size = next_size(size);
		if (size <= _size) return;
		std::vector<Node*> newTable(size, nullptr);
		for (Node* node : _table) {
			while (node) {
				// int idx = _hf(node->data) % newTable.size();
				int idx = table_index(node->data, newTable.size());
				Node* next = node->next;
				node->next = newTable[idx];
				newTable[idx] = node;
				node = next;
			}
		}
		// _table = std::move(newTable);
		_table.swap(newTable);
		
	}

	// 拷贝
	hash_table(const hash_table& ht) {
		_size = ht.size();
		_table.resize(ht.table_size());
		Node* dummy = new Node;
		for (int i = 0;i < _table.size();++i) {
			Node* pre = dummy;
			Node* node = ht._table[i];
			while (node != nullptr) {
				pre->next = new Node(node->data);
				node = node->next;
				pre = pre->next;
			}
			_table[i] = dummy->next;
			dummy->next = nullptr;
		}
		delete dummy;
	}
	hash_table(hash_table&& ht) {
		std::swap(_size, ht._size);
		_table.swap(ht._table);
	}
	hash_table& operator=(hash_table ht) {
		swap(ht);
		return *this;
	}


public:
	Node* find(const Key& key)const {
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		for (Node* node = _table[idx];node;node = node->next) {
			if (node->data == key) return node;
		}
		return nullptr;
	}

	pair<Node*, bool> insert(const Key& key) {
		if (_size == _table.size()) {
			//扩容table
			resize(_size * 2);
		}
		// 取得下标
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		if (_table[idx] == nullptr) {
			_table[idx] = new Node(key);
		}
		else {
			for (Node* node = _table[idx];node != nullptr;node = node->next) {
				// key已经存在就直接返回
				if (node->data == key) return make_pair(node, false);
			}
			Node* node = new Node(key);
			// 头插
			node->next = _table[idx];
			_table[idx] = node;
		}
		++_size;
		return make_pair(_table[idx], true);
	}


	void erase(const Key& key) {
		// int idx = _hf(key) % _table.size();
		int idx = table_index(key);
		Node* dummy = new Node;
		dummy->next = _table[idx];
		Node* pre = dummy, * cur = dummy->next;
		while (cur) {
			if (cur->data == key) {
				pre->next = cur->next;
				_table[idx] = dummy->next;
				delete cur;
				--_size;
				break;
			}
			pre = cur;
			cur = cur->next;
		}
		delete dummy;
	}


public:
	void print()const {
		int idx = 0;
		for (Node* node : _table) {
			cout << idx++ << ": ";
			while (node) {
				cout << node->data << " -> ";
				node = node->next;
			}
			cout << "null" << endl;
		}
		cout << endl;
	}

};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1614716.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何使用渐变块创建自定义聊天机器人

如何使用渐变块创建自定义聊天机器人

如何使用渐变块创建自定义聊天机器人 文章目录 如何使用渐变块创建自定义聊天机器人一、介绍二、参考示例1、一个简单的聊天机器人演示2、将流式传输添加到您的聊天机器人3、喜欢/不喜欢聊天消息4、添加 Markdown、图像、音频或视频 一、介绍 **重要提示&#xff1a;**如果您刚…
阅读更多...
《你想活出怎样的人生》上映，AOC带你打开宫崎骏的动画世界大门！

《你想活出怎样的人生》上映，AOC带你打开宫崎骏的动画世界大门！

摘要&#xff1a;宫崎骏式美学&#xff0c;每一帧都是治愈&#xff01; 近日&#xff0c;宫崎骏新作《你想活出怎样的人生》正式公映。苍鹭与少年的冒险、奇幻瑰丽的场景、爱与成长的主题&#xff0c;让观众们收获到满满的爱与感动。宫崎骏总能以细腻的画面、温柔的音乐&#…
阅读更多...
LeetCode - 面试题 08.06. 汉诺塔问题

LeetCode - 面试题 08.06. 汉诺塔问题

目录 题目链接 解题思路 解题代码 题目链接 LeetCode - 面试题 08.06. 汉诺塔问题 解题思路 假设 n 1,只有一个盘子&#xff0c;很简单&#xff0c;直接把它从 A 中拿出来&#xff0c;移到 C 上&#xff1b; 如果 n 2 呢&#xff1f;这时候我们就要借助 B 了&#xff0c;因…
阅读更多...
select实现echo服务器的并发

select实现echo服务器的并发

select实现echo服务器的并发 代码实现 #include <stdio.h> #include <string.h> #include <sys/types.h> #include <sys/socket.h> #include <stdlib.h> #include <arpa/inet.h> #include <sys/select.h> #include <sys/time.h…
阅读更多...
14. Spring AOP（二）实现原理

14. Spring AOP（二）实现原理

源码位置&#xff1a;spring_aop 上一篇文章中我们主要学习了AOP的思想和Spring AOP使用&#xff0c;本文讲的是Spring是如何实现AOP的&#xff0c;Spring AOP是基于动态代理来实现AOP的&#xff0c;在将动态代理之前先来了解一下什么是代理模式。 1. 代理模式 在现实中就有许…
阅读更多...
【算法刷题 | 回溯思想 07】4.18（全排列、全排列 ||）

【算法刷题 | 回溯思想 07】4.18（全排列、全排列 ||）

文章目录 11.全排列11.1题目11.2解法&#xff1a;回溯11.2.1回溯思路&#xff08;1&#xff09;函数返回值以及参数&#xff08;2&#xff09;函数返回值&#xff08;3&#xff09;遍历过程 11.2.2代码实现 12.全排列 ||12.1题目12.2解法&#xff1a;回溯12.2.1回溯思路12.2.3代…
阅读更多...
教师编制可以跨市调动吗

教师编制可以跨市调动吗

在教育的广阔天地中&#xff0c;我们常常面临各种职业发展的选择。作为一名教师&#xff0c;是否能够实现跨市调动&#xff0c;这不仅是一个职业发展的问题&#xff0c;更关系到个人生活和职业规划的诸多方面。今天&#xff0c;我们就来探讨一下&#xff0c;拥有编制身份的教师…
阅读更多...
2024免费专为Mac用户设计的清理和优化工具CleanMyMac X

2024免费专为Mac用户设计的清理和优化工具CleanMyMac X

CleanMyMac X是一款专为Mac用户设计的清理和优化工具。以下是对CleanMyMac X的详细介绍&#xff1a; 一、主要功能 系统清理&#xff1a;CleanMyMac X能够智能扫描Mac的磁盘空间&#xff0c;识别并清理各种垃圾文件&#xff0c;这些垃圾文件包括重复文件、无用的语言安装包、i…
阅读更多...
模拟信号的离散化

模拟信号的离散化

本文介绍模拟信号的离散化。 1.采样定理 定义&#xff1a;若想重建输入的模拟信号&#xff0c;采样频率必须大于等于输入模拟信号最高频率的2倍&#xff0c;即&#xff1a; 其中&#xff0c;为采样频率&#xff0c;为输入模拟信号最高频率 否则&#xff0c;信号会发生混叠 2…
阅读更多...
攻防世界---misc---easycap

攻防世界---misc---easycap

1.下载附件是一个流量包&#xff0c;拿到wireshark中分析 2.查看分级协议 3.过滤data 4.追踪tcp流 5.得到flag
阅读更多...
EUV光刻机机密文件被盗 | 百能云芯

EUV光刻机机密文件被盗 | 百能云芯

4月22日消息&#xff0c;据法国媒体LeMagIT报道&#xff0c;日本光学技术领导厂商 Hoya Corporation&#xff08;豪雅&#xff09;最近遭遇了勒索软件的攻击&#xff0c;其总部和多个业务部门的IT系统遭受波及。据称超过 170 万份内部文件流失&#xff0c;其包括EUV掩模坯料和光…
阅读更多...
根据表格该列数据的长度动态变化该列的宽度；

根据表格该列数据的长度动态变化该列的宽度；

提示：记录工作中遇到的需求及解决办法 文章目录 前言一、代码前言 在使用elementui的表格将数据展示出来时，我们想根据表格该列数据的长度动态变化该列的宽度； 1.看了一下elementui文档有一个 width 的属性，可用它来修改对应列。 2.那么我们需要拿到该列的所有数据去比较…
阅读更多...
1V1论文辅导 | 涉及3DGS、NeRF、深度学习+结构光、SLAM、三维场景理解、扩散模型、6D位姿估计、强化学习、计算机视觉……

1V1论文辅导 | 涉及3DGS、NeRF、深度学习+结构光、SLAM、三维场景理解、扩散模型、6D位姿估计、强化学习、计算机视觉……

阅读更多...
为何3D动画工作室偏爱使用在线渲染农场?

为何3D动画工作室偏爱使用在线渲染农场?

随着市场需求的不断增长和生产挑战的加剧&#xff0c;3D动画工作室面临着前所未有的压力。为了有效应对这些挑战&#xff0c;众多工作室选择了使用网络渲染农场。这种选择使他们能够借助网络渲染农场的强大渲染能力和高度灵活的资源配置&#xff0c;以此优化他们的工作流程&…
阅读更多...
JAVA学习笔记27（异常）

JAVA学习笔记27（异常）

1.异常 ​ *异常(Exception) ​ *快捷键 ctrl alt t 选中try - catch ​ *如果进行了异常处理&#xff0c;那么即使出现了异常&#xff0c;程序可以继续执行 1.1 基本概念 ​ *在Java语言中&#xff0c;将程序执行中发生的不正常情况称为"异常"(开发过程中的语…
阅读更多...
Spring Boot 自动装配执行流程

Spring Boot 自动装配执行流程

Spring Boot 自动装配执行流程 Spring Boot 自动装配执行流程如下&#xff1a; Spring Boot 启动时会创建一个 SpringApplication实例&#xff0c;该实例存储了应用相关信息&#xff0c;它负责启动并运行应用。实例化 SpringApplication 时&#xff0c;会自动装载META-INF/spr…
阅读更多...
HarmonyOS ArkUI滚动类组件-List、ListItem

HarmonyOS ArkUI滚动类组件-List、ListItem

List 是很常用的滚动类容器组件之一&#xff0c;它按照水平或者竖直方向线性排列子组件&#xff0c; List 的子组件必须是 ListItem &#xff0c;它的宽度默认充满 List 的宽度。 List定义介绍 interface ListInterface {(value?: { initialIndex?: number; space?: numbe…
阅读更多...
隐藏表头和最高层级的复选框

隐藏表头和最高层级的复选框

隐藏表头和最高层级的复选框 <!-- 表格 --><el-tableref"tableRef"v-loading"tableLoading"default-expand-allclass"flex-1 !h-auto"row-key"regionId":header-cell-class-name"selectionClass":row-class-name&q…
阅读更多...
HarmonyOS ArkUI实战开发-窗口模块（Window）

HarmonyOS ArkUI实战开发-窗口模块（Window）

窗口模块用于在同一物理屏幕上&#xff0c;提供多个应用界面显示、交互的机制。 对应用开发者而言&#xff0c;窗口模块提供了界面显示和交互能力。对于终端用户而言&#xff0c;窗口模块提供了控制应用界面的方式。对于操作系统而言&#xff0c;窗口模块提供了不同应用界面的…
阅读更多...
深度学习500问——Chapter08：目标检测（3）

深度学习500问——Chapter08：目标检测（3）

文章目录 8.2.7 DetNet 8.2.8 CBNet 8.2.7 DetNet DetNet是发表在ECCV2018的论文&#xff0c;出发点是现有的检测任务backbone都是从分类任务衍生而来的&#xff0c;因此作者想针对检测专用的backbone做一些讨论和研究而设计了DetNet&#xff0c;思路比较新奇。 1. Introduct…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023