A1/A2. Gardener and the Capybaras (easy version)


三个字符串,按照顺序连在一起,三个字符串满足第二个字符串大于等于第一个和第三个,或者第二个字符串小于等于第一个和第三个,输出满足情况的三个字符串。
思路:对于长度为3的字符串,三个字符串长度都只能为1,特判一下;对于其他情况,如果除了第一个字母和最后一个字母,中间的存在a,那可以输出a和前面的字符串,以及后面的字符串;若是不存在a,则输出第一个字母和最后一个字母,中间的直接输出即可,这样可以满足中间的字符串的条件。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int t;
std::string s;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> s;
int len = s.length();
if(len == 3) {
if(s[0] >= s[1] && s[2] >= s[1] || s[0] <= s[1] && s[2] <= s[1])
std::cout << s[0] << ' ' << s[1] << ' ' << s[2] << '\n';
else
std::cout << ":(" << '\n';
continue;
}
int pos = -1;
for(int i = 1; i < len - 1; i ++) {
if(s[i] == 'a') {
pos = i;
break;
}
}
if(pos != -1) {
for(int i = 0; i < pos; i ++) {
std::cout << s[i];
}
std::cout << ' ';
std::cout << 'a' << ' ';
for(int i = pos + 1; i < len; i ++) {
std::cout << s[i];
}
std::cout << '\n';
continue;
}
std::cout << s[0] << ' ';
for(int i = 1; i < len - 1; i ++) {
std::cout << s[i];
}
std::cout << ' ';
std::cout << s[len - 1] << '\n';
}
return 0;
}B. Gardener and the Array


给出数组a,但是给出的形式是对于每个数字,给出二进制下哪些位是1, 判断存不存在两个不同的子序列,使得子序列的或和相等。
思路:只要存在一个数,它的每一位1都不是唯一存在的即可满足条件。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int t, n, u, x;
std::vector<int> a[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n;
std::map<int, int> mp;
for(int i = 1; i <= n; i ++)
a[i].clear();
for(int i = 1; i <= n; i ++) {
std::cin >> x;
for(int j = 1; j <= x; j ++) {
std::cin >> u;
mp[u] ++;
a[i].push_back(u);
}
}
bool flag = false;
for(int i = 1; i <= n; i ++) {
bool f = true;
for(auto u : a[i]) {
if(mp[u] == 1) {
f = false;
break;
}
}
if(f) {
flag = true;
break;
}
}
std::cout << (flag ? "Yes" : "No") << '\n';
}
return 0;
}os:因为memset被卡TLE了好几发,很难过
C. Interesting Sequence
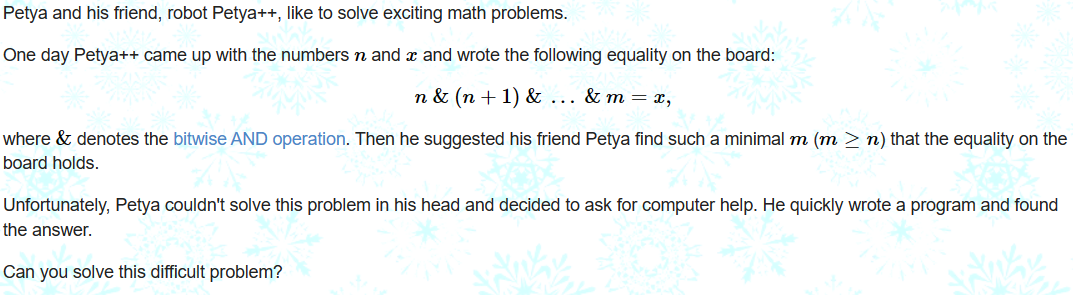

给出n和x,求最小的m使得n & (n + 1) & (n + 2) & ... & m = x。
思路:按位考虑是最简单的。
(1)n该位为0,x该位也为0,m的选值没有影响;
(2)n该位为0,x该位为1,不可能满足,输出-1;
(3)n该位为1,x该位为0,需要等到该位是0的数字出现才可满足条件,设该数为k,则在现有的范围与大于等于k取交集;
(4)n该位为1,x该位也为1,需要在该位变成0之前取值,这样可以取到一个最大值k,则在现有的范围与小于等于k取交集。
AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 1e5 + 5;
int t;
ll n, x;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n >> x;
std::bitset<64> a(n), b(x);
ll l = n, r = 3e18;
for(int i = 63; i >= 0; i --) {
if(!a[i] && b[i]) {
l = r + 1;
break;
}
if(!a[i] && !b[i]) continue;
if(a[i] && !b[i])
l = std::max(l, ((n / ((ll)1 << i)) + 1) * ((ll)1 << i));
else
r = std::min(r, ((n / ((ll)1 << i)) + 1) * ((ll)1 << i) - 1);
}
if(l <= r)
std::cout << l << '\n';
else
std::cout << -1 << '\n';
}
return 0;
}E. The Human Equation


给出数组,可以对数组进行两种操作:选择一个子数组,并对其中偶数位置的数-1,奇数位置的数+1;
选择一个子数组,并对其中奇数位置的数-1,偶数位置的数+1,问将所有数字全部变为0所需最少的操作次数。
思路:学习佬的思路

AC Code:
#include <bits/stdc++.h>
typedef long long ll;
const int N = 2e5 + 5;
int t, n;
ll a[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin >> t;
while(t --) {
std::cin >> n;
ll x = 0, y = 0;
ll ans = 0;
for(int i = 1; i <= n; i ++) {
std::cin >> a[i];
if(a[i] > 0) {
ll res = std::min(a[i], y);
y -= res;
a[i] -= res;
ans += a[i];
x += a[i] + res;
}
if(a[i] < 0) {
a[i] = -a[i];
ll res = std::min(a[i], x);
x -= res;
a[i] -= res;
ans += a[i];
y += a[i] + res;
}
}
std::cout << ans << '\n';
}
return 0;
}