感谢大佬的光临各位,希望和大家一起进步,望得到你的三连,互三支持,一起进步
个人主页:LaNzikinh-CSDN博客
收入专栏:初阶数据结构_LaNzikinh篮子的博客-CSDN博客
文章目录
- 前言
- 一.快速排序非递归
- 二.数据结构栈与内存栈
- 三.计数排序
- 四.稳定性
- 总结
前言
计算机在实现递归时会调用系统的堆栈,这很消耗计算机内存资源,所以采用非递归算法的本质就是手动模拟系统的堆栈调用来降低computer资源的消耗,有时候还会造成栈溢出所以这些厉害的排序我们都要掌握他的非递归,然后在在补充一个计数排序。
一.快速排序非递归
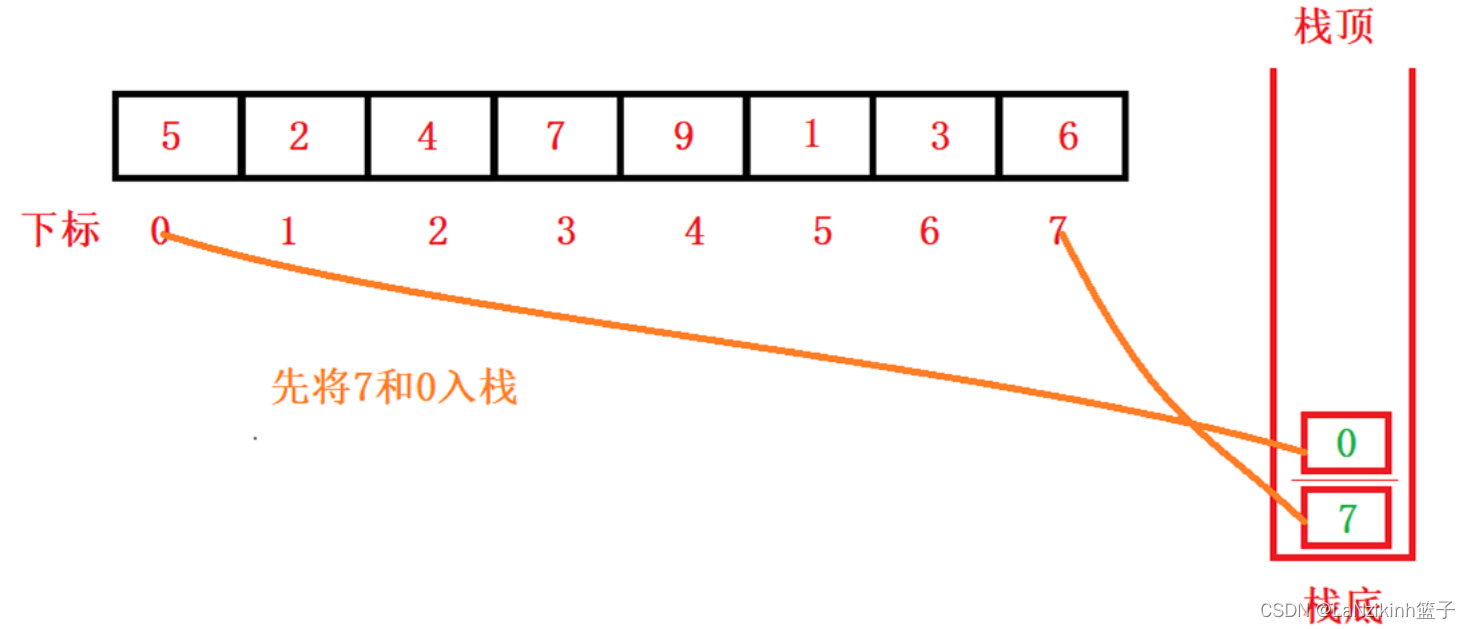
递归改非递归有两种改法,一种是改循环,还有一种就是通过数据结构来转换,我们之前的归并排序非递归就是通过改循环,这次就是通过栈,去搭建
思路:先搭建一个栈,利用栈的特点,后进先出,先入右,在入左若左右存在有序,则有序不排
#include<stdio.h>
void QuickSortNonR(int* a, int n)
{
//创建栈,初始化一个栈
ST st;
stackInit(&st);
//先入右,在入左
stackPush(&st, n - 1);
stackPush(&st,0);
//检查栈里还有没有元素
while (!stackEmpty(&st))
{
//拿左边的值,因为是先入右,在入左,所以可以拿到
int left = stackTop(&st);
stackPop(&st);
int right= stackTop(&st);
stackPop(&st);
//进行一次快排
int keyIndex = Quick1sort(a, left, right);
//如果中间右边的数小于最右,就继续入栈
if (keyIndex + 1 < right)
{
stackPush(&st, right);
stackPush(&st, keyIndex + 1);
}
//同理
if (left < keyIndex - 1)
{
stackPush(&st, keyIndex - 1);
stackPush(&st, left);
}
}
//最后销毁栈
stackDestory(&st);
}这样利用数据结构搭建,大的减少了栈空间的利用,减少了大量的函数调用,不会栈溢出
二.数据结构栈与内存栈
很多人不理解,这个栈溢出和数据结构里我们写的栈有什么区别,一个是栈区,一个是数据结构线性表,这两个不是一个东西,计算机内存分为四个区域,代码区,静态区,栈区和堆区

- 代码区:存放函数体的二进制代码,由操作系统管理创建,代码区时共享的,对于频繁被执行的程序,只需要存有一份代码即可;
- 静态区:存放全局变量和静态变量以及常量,在程序结束后由操作系统释放;
- 栈区:由编译其自动分配释放,存放函数的参数值以及局部变量等;
- 堆区:一般由程序员通过 new 开辟空间,进行分配和释放,若程序员不释放,则程序结束时由操作系统回收通俗一点就是,栈区就是函数和函数调用,堆区就是动态开辟,栈区内容小,堆区内容大
所以多次开辟内存是可以的,但是要记得释放,但是多次函数调用会让栈的空间满,之后就溢出了,没有栈的空间了
而数据结构的栈它就是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表,特点是后进先出
所以这两个不是一个东西,不用搞混了
三.计数排序
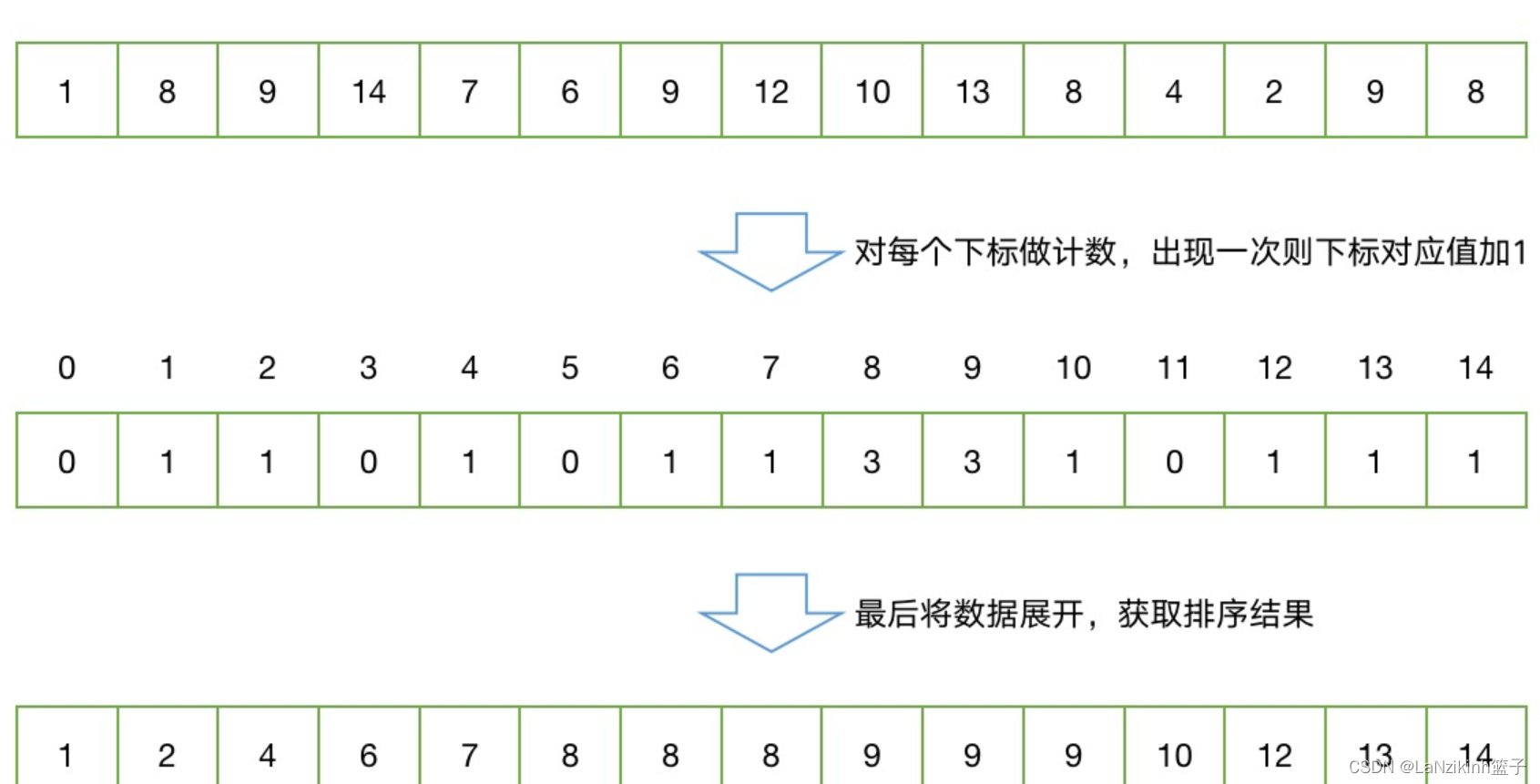
计数排序顾名思义,就是通过计数来排序的一种排序算法,他和我们之前的算法不一样,计数排序是一种非比较排序算法,适用于整数或有限范围内的非负整数排序,它的基本思想是统计数组中每个元素出现的次数,然后根据出现次数重新构造有序序列。
思路:计数排序使用一个额外的数组,来记录次数,把带排序的数字统计到额外数组中去,最后用额外数组来反映顺序
但是有缺陷,如果我是从100开始的5个数字,101,102,...105,难道我要开辟105个空间吗?
我们之前这种思路是求的绝对映射位置,我们现在要相对的映射位置,这样才能节省空间用
最大的减最小的加1来开辟范围
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);开辟范围来计数,用memset来初始化,当然直接用calloc函数也是可以的
总代码思路:求出最大最小值,利用最大与最小值,开辟空间,遍历一遍,统计次数,利用次数得出顺序
#include<stdio.h>
#include<stdlib.h>
void CountSort(int* a, int n)
{
//求出最大最小值
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
//利用最大与最小值,开辟空间
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
memset(count, 0, sizeof(int) * range);
//遍历一遍,统计次数
for (int i = 0; i < n; i++)
{
//注意要减去最小值
count[a[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
//前面减了现在要加上
a[j] = i + min;
j++;
}
}
free(count);
}计数排序的时间复杂度为O(N+range),所以要求的范围越小这个排序效果越好
四.稳定性
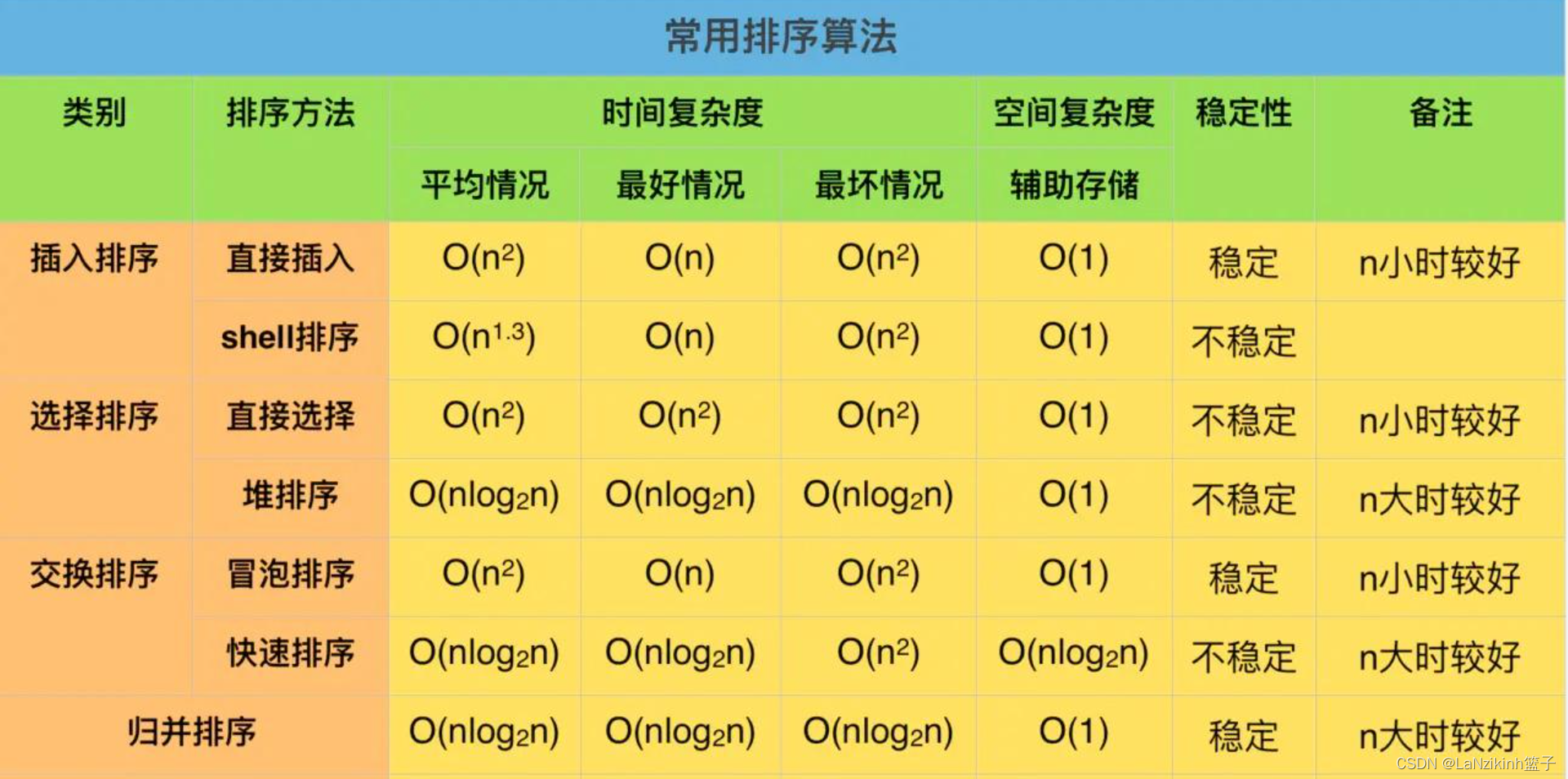
定义:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri=rj,且ri在rj之前,而在排序后的序列中,ri仍在rj之前,则称这种排序算法是稳定的;否则称为不稳定的
注意:堆排序、快速排序、希尔排序、直接选择排序不是稳定的排序算法,而基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。
总结
初级的排序算法就是这些了,还有一些不常用的和一些难的,等学了更多的知识我们再去了解