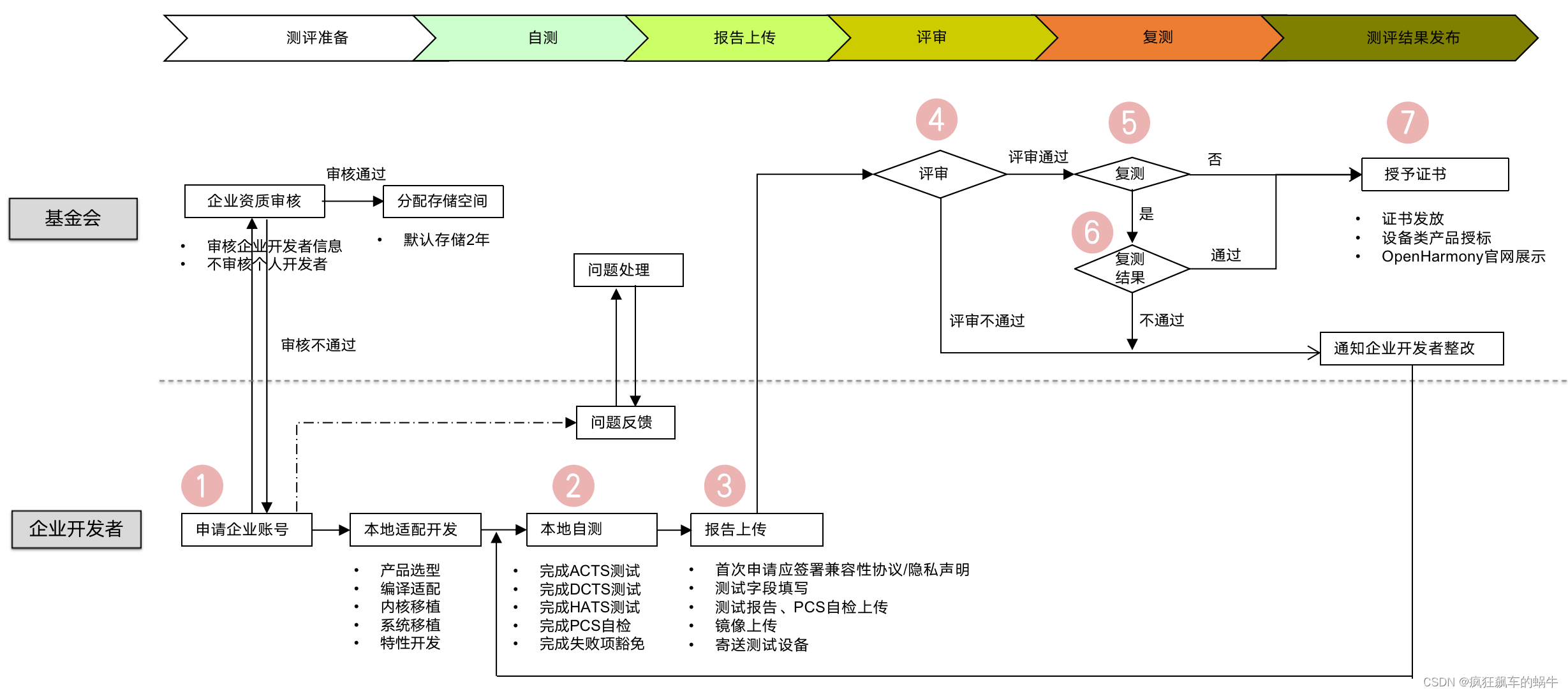
题目描述

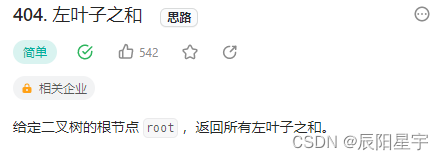
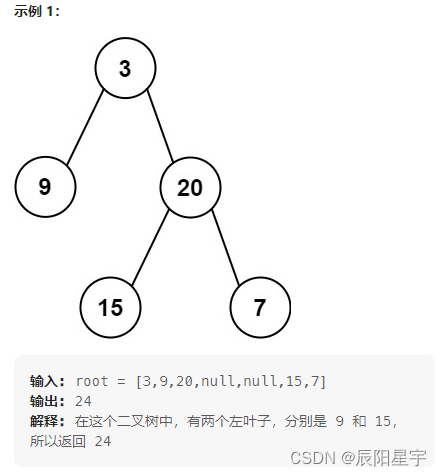
在这里插入图片描述

原题链接：404. 左叶子之和

解题思路

一、递归法

（1）设置一个布尔变量判定（先序遍历）

左孩子一定在每个子树的最左侧，因此设置一个局部参数flag，当每次遍历的是左子树时，令其为true。每一层接受上一层传来的flag信息进行判定。当遍历到叶子节点时，若flag==ture说明为左孩子，相加。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;        // 当
    void leftSum(TreeNode* root, bool flag) {
        if(!root->left && !root->right) {
            if(flag == true)
                res += root->val;
            return ;
        }
        if(root->left) {
            leftSum(root->left, true);         //      
        }   
        if(root->right) {
            leftSum(root->right, false);
        }   
    }
    int sumOfLeftLeaves(TreeNode* root) {
        leftSum(root, false);
        return res;
    }
};

时间复杂度 $O (n)$
时间复杂度 $O (n)$

（2）根据左叶子结构特点（先序+后序遍历）

提前判定左叶子，当发现该节点的后续结点有左叶子特征：左孩子存在、左孩子的左孩子与左孩子的右孩子不存在，则就将这个叶子结点的值相加。

先序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;
    int sumOfLeftLeaves(TreeNode* node) {        
        if(node->left && !node->left->left && !node->left->right) {
            res += node->left->val;            
        } else if (node->left) {
            sumOfLeftLeaves(node->left);
        }
        if(node->right)
            sumOfLeftLeaves(node->right);
        return res;
    }
};

后序遍历
采用后续遍历的方式，遍历左，遍历右，将结果返回给上一个结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        // 当以空节点为结束条件时，相加操作通常在最后面
        // 当以叶子结点为结束条件时，相加操作通常在该条件操作。        
        if(!root)       return 0;
        int leftValue = 0;
        // 找到后续会有为左叶子结点，则进行相加
        if(root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
            leftValue = root->left->val;
        }
        // 向下继续遍历（后序遍历）
        return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
    }
};

2、迭代法

（1）先序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int res = 0;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            if(node->left && !node->left->left && !node->left->right)
                res += node->left->val;
            if(node->left)      st.push(node->left);
            if(node->right)     st.push(node->right);
        }
        return res;
    }
};

（2）层次遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        queue<TreeNode*> que;
        que.push(root);
        int res = 0;
        while(!que.empty()) {
            TreeNode* node = que.front();
            que.pop();
            if(node->left && !node->left->left && !node->left->right) {
                res += node->left->val;
            }
            if(node->left)      que.push(node->left);
            if(node->right)     que.push(node->right);
        }
        return res;
    }
};