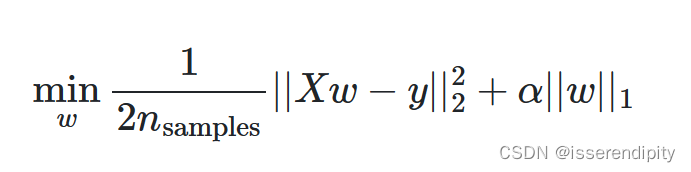前言:
上一节大概讲解了几种学习方式,下面几张就具体来讲讲监督学习的几种算法。
以下示例中
和
都是权重的意思!!!
注:本文如有错误之处,还请读者指出,欢迎评论区探讨!
1 线性模型(Linear Models)
1.1 普通最小二乘法(Ordinary Least Squares)
概念:
残差平和和最小
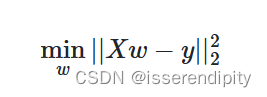
推导:
由于懒得打公式,我们直接引用别人的(图片来源)
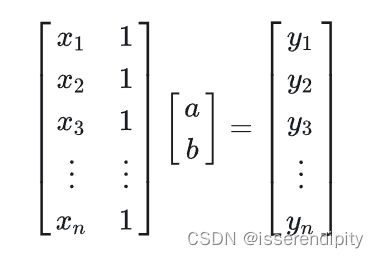
(1)先给出一个线性方程组

(2)改写成矩阵形式
(3)转化为一般形式
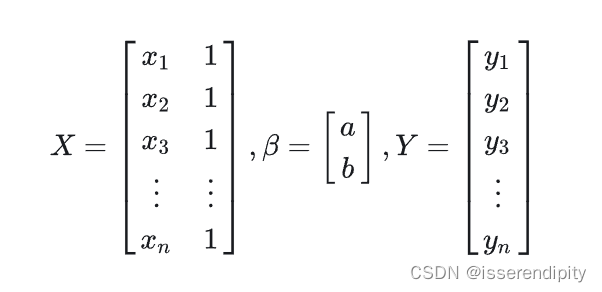
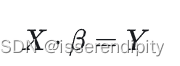
一般这个解都无精确解,只有最佳近似解,即超定方程。
(4)求偏导求(一般来说,这个不需要我们手动求,调包就可以了,嘿嘿,调包侠)
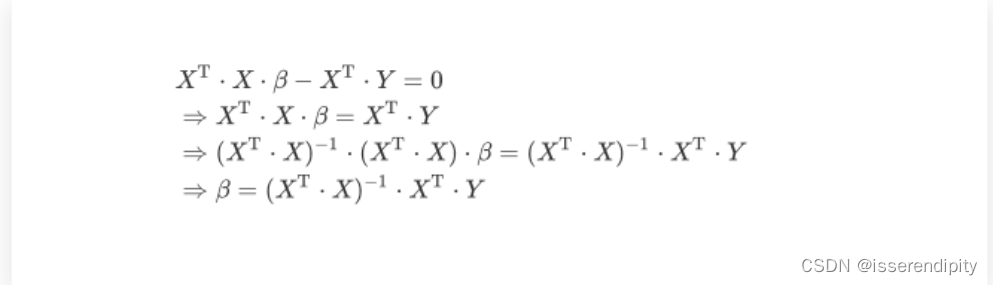
(5)最小二乘公式
因为是超定方程,有许多近似解,但是残差平方和最小的通常只有一个,我们就规定这个就是最优近似解。
示例:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# diabetas_X有442条样本,10个属性
diabetas_X, diabetas_Y = datasets.load_diabetes(return_X_y=True)
# 重新选取数据集,选取全部样本和前两个属性,并增加一维
diabetas_X = diabetas_X[:, np.newaxis, 2]
# 创建训练集和测试集
diabetas_X_train = diabetas_X[:-20]
diabetas_X_test = diabetas_X[-20:]
# 创建训练标签和真实的测试标签
diabetas_Y_train = diabetas_Y[:-20]
diabetas_Y_test = diabetas_Y[-20:]
# 使用线性回归的方法进行预测
regr = linear_model.LinearRegression()
# 拟合数据
regr.fit(diabetas_X_train, diabetas_Y_train)
# 预测测试集
diabetas_Y_pred = regr.predict(diabetas_X_test)
print("Coefficients:\n", regr.coef_) # 回归系数
print("Mean square error:%.2f" % mean_squared_error(diabetas_Y_test, diabetas_Y_pred)) # 平均平方误差
print("Coefficient of determination : %.2f" % r2_score(diabetas_Y_test, diabetas_Y_pred)) # 决定系数
plt.scatter(diabetas_X_test, diabetas_Y_test, color="black") # 点
plt.plot(diabetas_X_test, diabetas_Y_pred, color="red", linewidth=3) # 线
# 不显示x和y轴
plt.xticks(())
plt.yticks(())
plt.show()
结果:
Coefficients:
[938.23786125]
Mean square error:2548.07
Coefficient of determination : 0.47
拓展:
(1)非负最小二乘法(Non-Negative Least Squares):可将所有的系数约束为非负数,在现实中应用很多,如商品价格
(2)普通最小二乘复杂度(Ordinary Least Squares Complexity):
![]()
1.2 岭回归和岭分类(Ridge regression and classification)
该方法是普通最小二乘的一个变体。
岭分类的本质是将分类问题转化为回归问题,然后调用岭回归去解决。在此我们只讨论岭回归。
引入:
在使用线性模型拟合回归函数时,最终目的是想要求出的值,即最优近似解,更加直观的看到每个参数的权重大小,即重要性大小(权重大的,更重要),之后能够根据权重进行预测。
但是,当x多重共线的时候(即参数之间能够相互表示)的时候,那y的值就很难根据不同的x设计不同 的权重了。
不好理解是不是,上图!(图源)
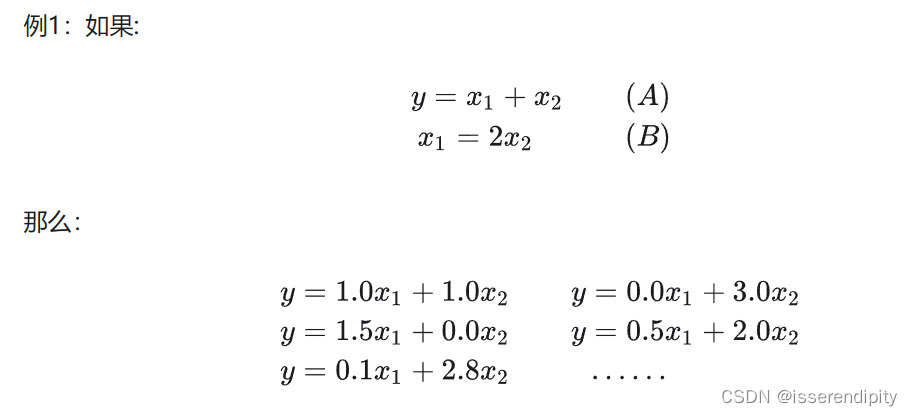
这张图很清楚,举得也是一个极端的例子,这两个x之前存在着精确的相关关系,即,导致有多种
满足这个式子。一般来说,x不会有这么精确地相关性,但是也足够迷惑了。
这个方法的目的是想把方差较小的参数投影到方差大的维度上,减少线性相关性,更好的拟合函数,进行预测。
概念:
在最小二乘的基础上加了一个惩罚项(L2-范式)。

这个为惩罚项的系数,认为控制,范围为
。
推导:
这推导过程使用了大量的线性代数,有奇异值分解,PCA等。
先用语言来描述一下,这个过程。我们先求出这个线性模型的特征值和特征向量,然后进行奇异值分解(求出对角矩阵,这个对角矩阵就是我们的构成的重要部分)和特征值分解(主成分分析PCA),找出主成分方向的第一主成分,进行投影,再垂直于第一主成分的面上找方差最大的第二主成分,进行投影,一直重复,直到n维结束。然后预测值就会根据
值和新的坐标来重新预测。
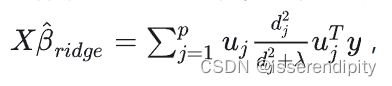
语言描述模糊?不理解?下面来图解(图片引用,这个博主还有详细的公式注解讲的非常棒):

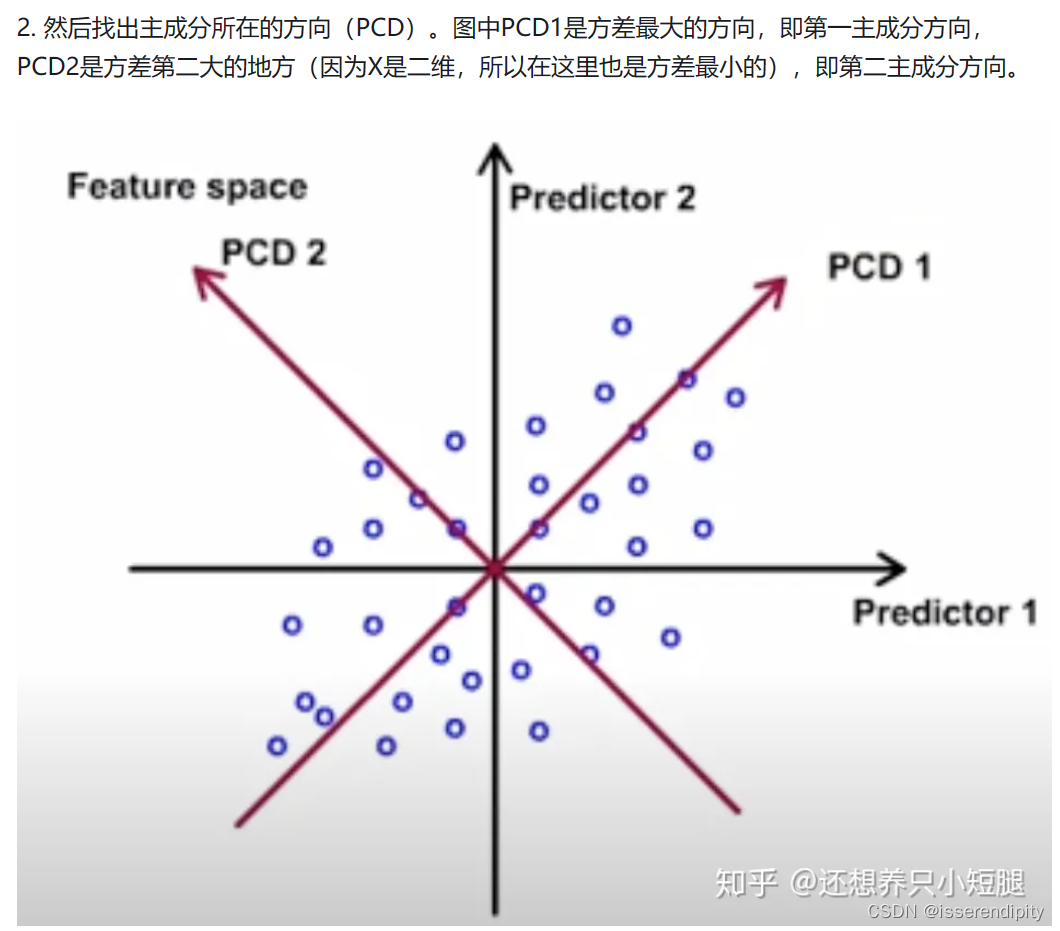
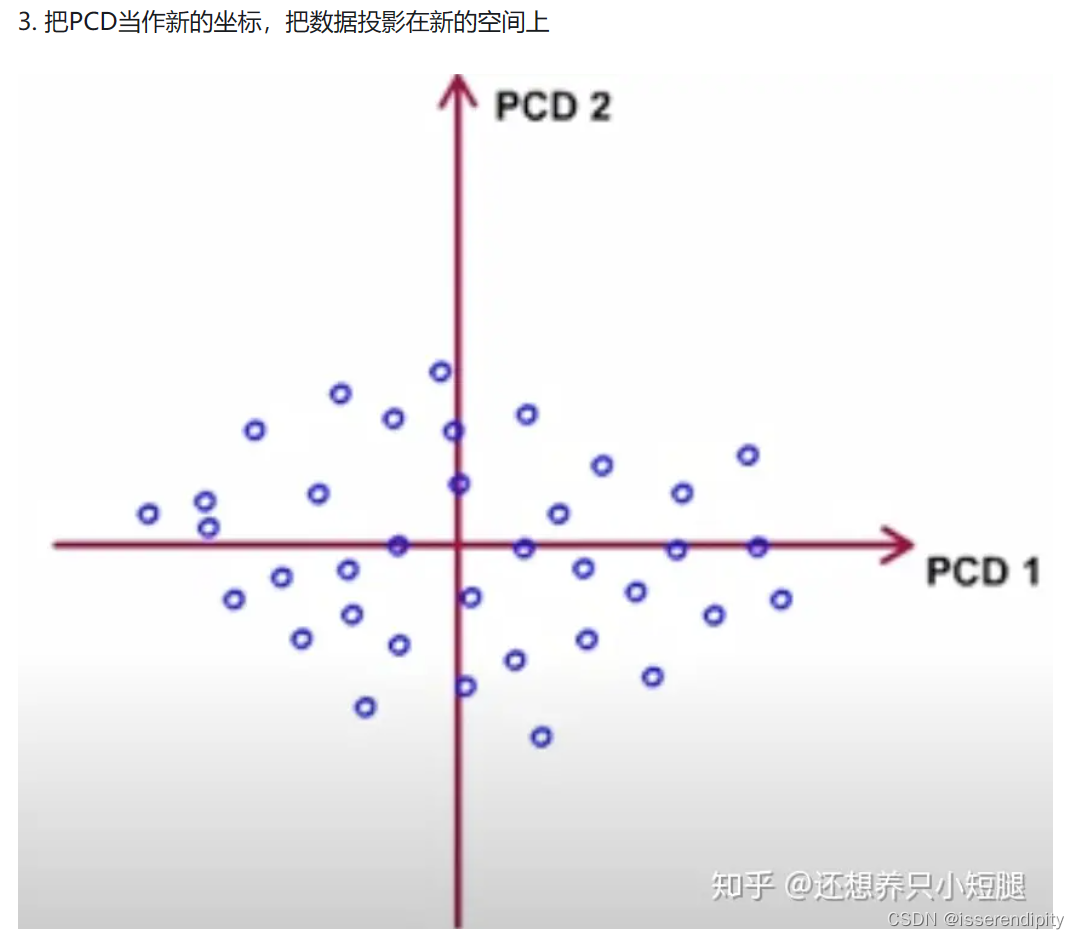
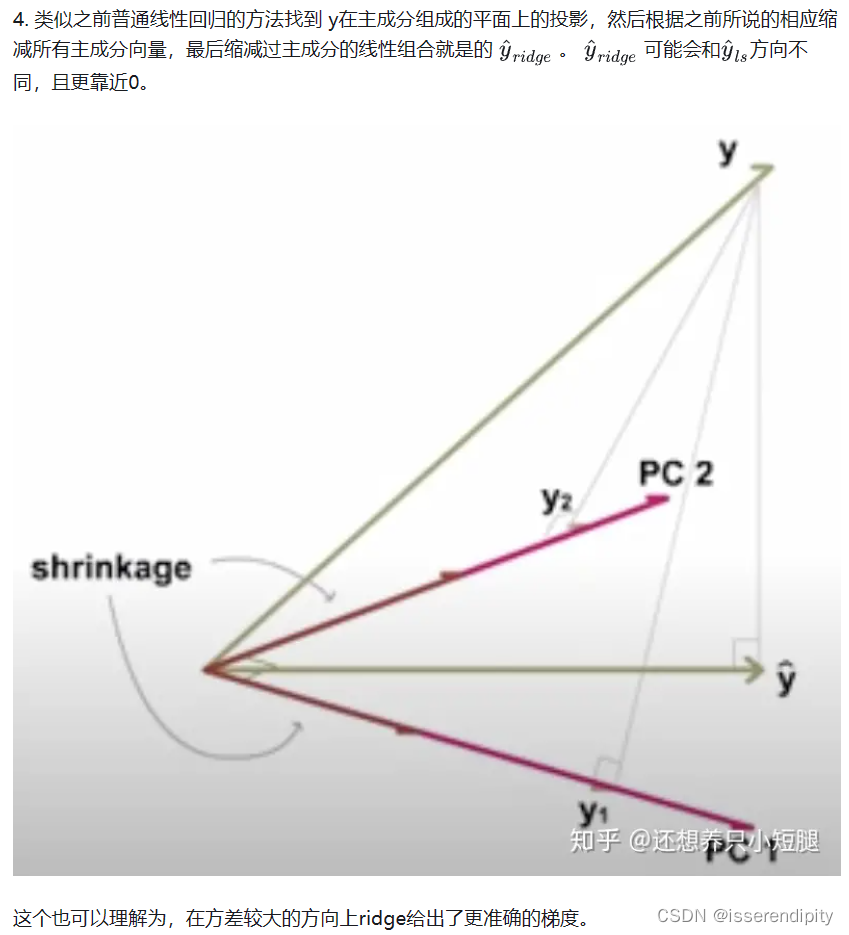
这样就实现了岭回归的功能。
示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# 创建一个 Ridge 回归模型
reg = linear_model.Ridge(alpha=0.5)
# 训练数据
X_train = np.array([[0, 0], [0, 0], [1, 1]])
y_train = np.array([0, 0.1, 1])
# 拟合模型
reg.fit(X_train, y_train)
# 获取回归系数和截距
coef = reg.coef_
intercept = reg.intercept_
# 绘制数据点
plt.scatter(X_train[:, 0], y_train, color='blue', label='Data Points')
# 绘制模型拟合的直线
x_line = np.linspace(0, 1, 100)
y_line = coef[0] * x_line + coef[1] * x_line + intercept
plt.plot(x_line, y_line, color='red', linewidth=2, label='Regression Line')
# 添加标签和图例
plt.xlabel('Feature 1')
plt.ylabel('Target')
plt.title('Linear Regression with Ridge Regularization')
plt.legend()
# 显示图形
plt.show()
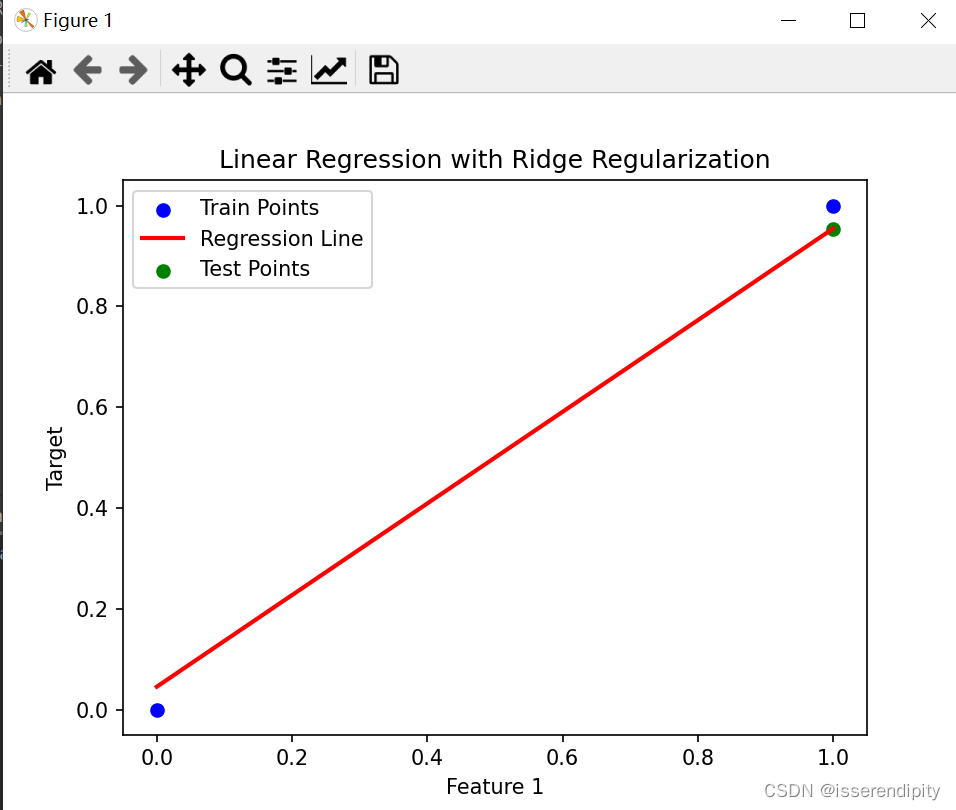
这是岭回归的结果(鲁棒性较好),比下面普通最小二乘(有点过于拟合了)的效果要好。
Ridge回归:
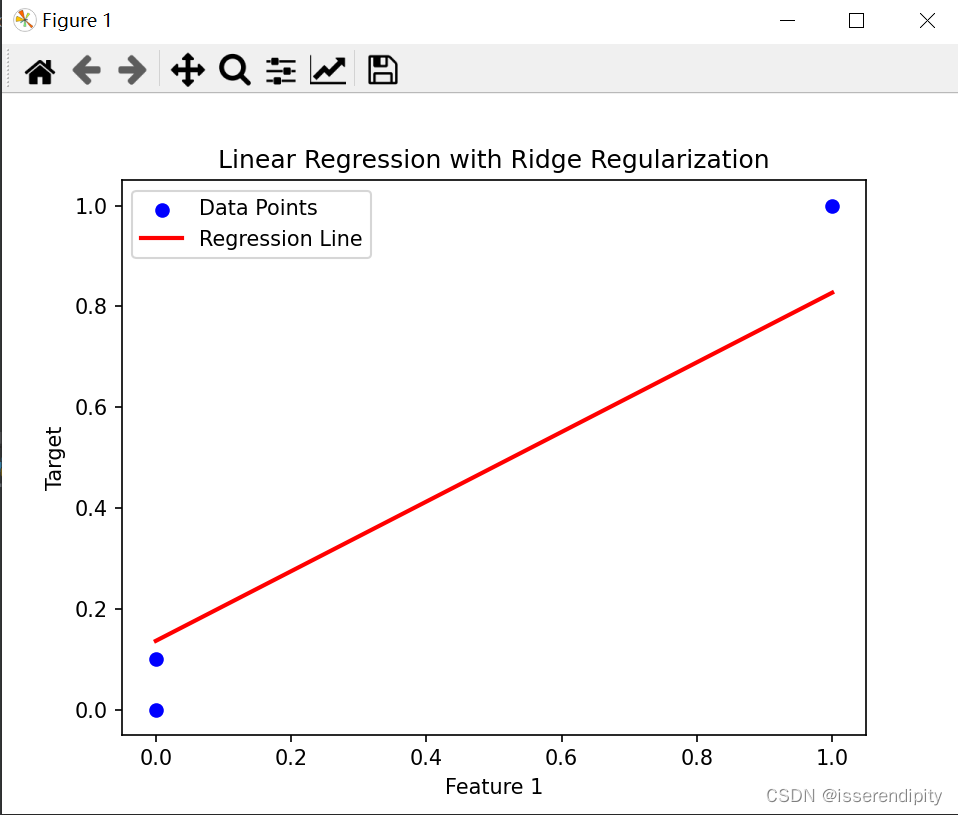
Oridinary回归:
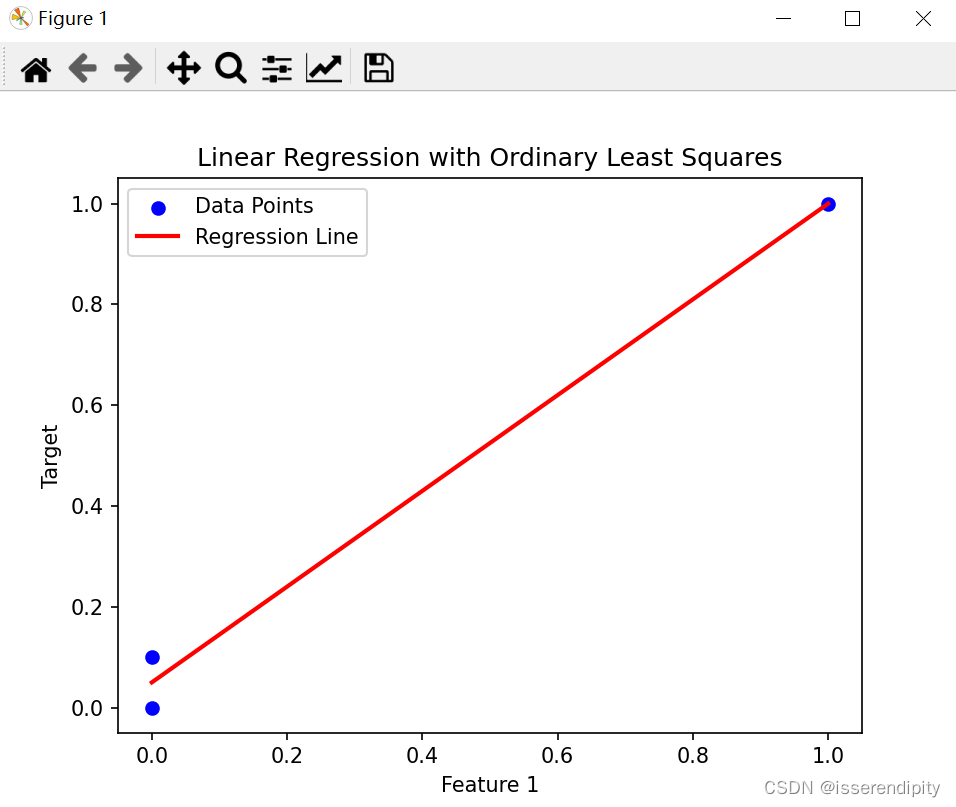
拓展:
(1)当越大(越靠左),惩罚越大,权重越趋近于0,
越小,后面的震动越大。
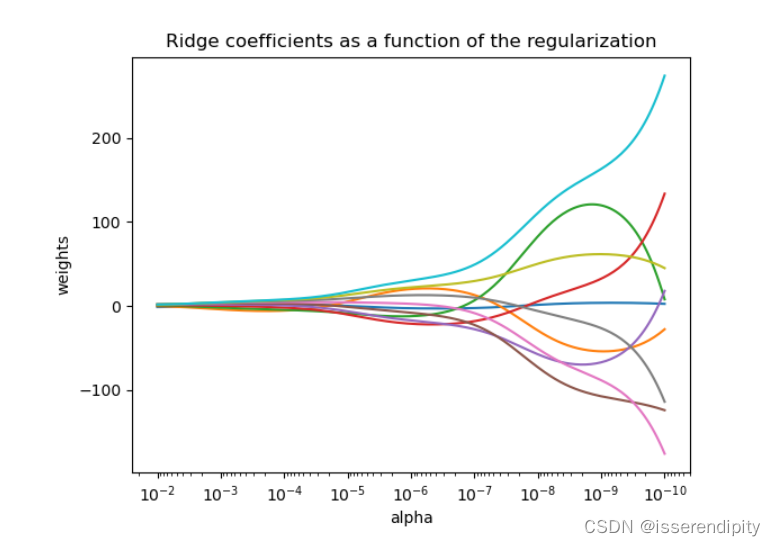
(2) 复杂度和普通最小二乘一样。
(3)留一交叉验证(leave-one-out Cross-Validation):从数据集D中,取出一组作为验证集,其他作为训练集,直到所有的样本都做过验证集,共计N次,最后对验证误差求平均。
1.1 套索算法(Lasso)
概念:
最小二乘解加L1-范式。
由于未知量比样本多,导致许多权重很小,就不是很重要。如果使用岭回归,这种不重要的变量也估计出来了,很容易导致过拟合。用Lasso方法,就可以把这些不重要变量的系数压缩为0,既实现了较为准确的参数估计,也实现了变量选择(降维)。
推导:
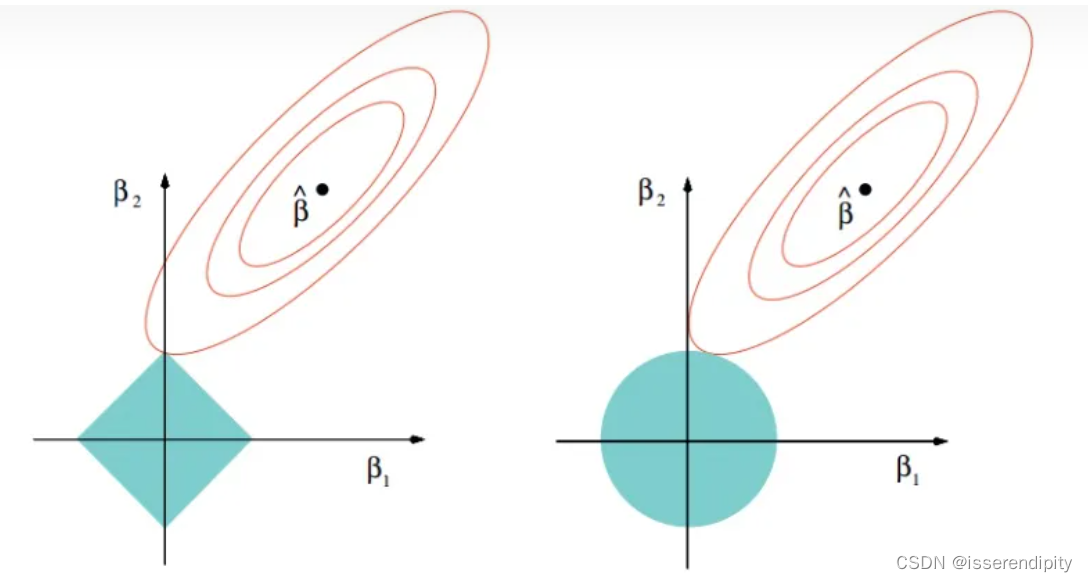
左为Lasso,右为岭回归,β1,β2是要优化的模型参数,红色椭圆为目标函数,蓝色区域是解空间。
该图可以看出来,Lasso的最优解更容易切到坐标轴上,而Ridge回归在不抛弃任何一个特征的情况下,缩小了回归系数,使模型相对比较稳定,但和Lasso相比,鲁棒性比较差。
示例:
import matplotlib.pyplot as plt
from sklearn import linear_model
import numpy as np
reg=linear_model.Ridge(alpha=0.1) #alpha惩罚系数
x_train=np.array([[0, 0], [1, 1]])
y_train=np.array([0,1])
x_test=np.array([[1,1]])
reg.fit(x_train,y_train)
y_pre=reg.predict(x_test)
coef=reg.coef_
intercept=reg.intercept_
plt.scatter(x_train[: ,0],y_train,color="blue",label="Train Points")
x_line=np.linspace(0,1,100)
y_line = coef[0] * x_line + coef[1] * x_line + intercept
plt.plot(x_line, y_line, color='red', linewidth=2, label='Regression Line')
plt.scatter(x_test[:,0],y_pre,color="green",label="Test Points")
plt.xlabel('Feature 1')
plt.ylabel('Target')
plt.title('Linear Regression with Ordinary Regularization')
plt.legend()
plt.show()绿色为预测的点,蓝色是原始数据点。根据图片来看,肯定是Lasso拟合的效果更好,更接近与现实。
Lasso回归:
Ridge回归:
Oridinary回归: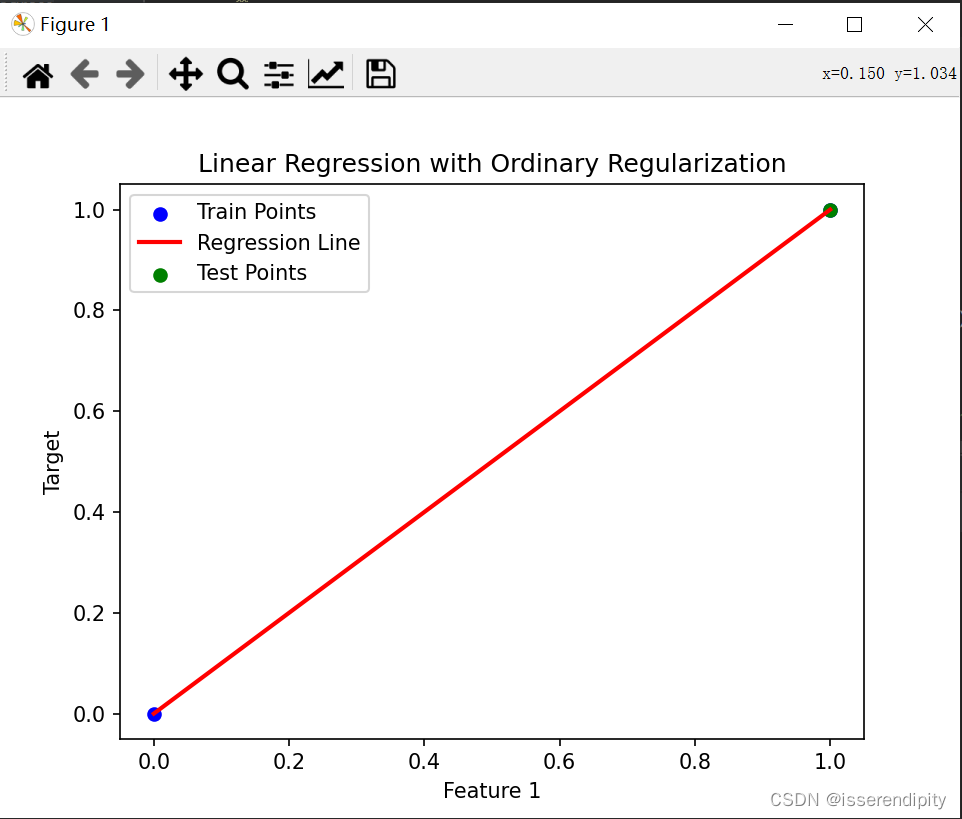
还有很多种线性模型,我们有时间再讨论,下面先介绍线性和二次判别。

2 线性和二次判别分析(Linear and Quadratic Discriminant Analysis)
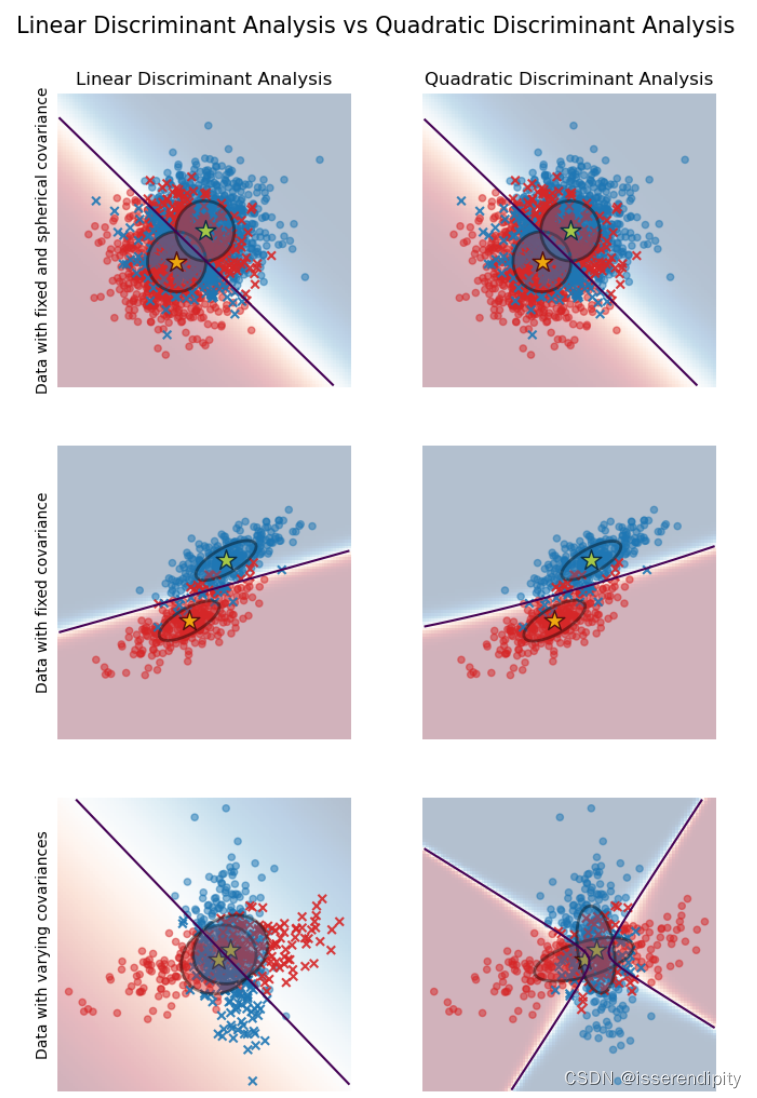
该图显示了线性判别分析和二次判别分析的决策边界。下面一行表明,线性判别分析只能学习线性边界,而二次判别分析可以学习二次边界,因此更加灵活。
2.1 使用LDA(线性判别)进行降维(Dimensionality reduction using Linear Discriminant Analysis)
概念:
这个最熟悉的应该就是Fisher判别了吧,哈哈哈
给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
一句话概括就是类内离散度小,类间离散度大。
推导(引用):


示例:
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris=datasets.load_iris()
x=iris.data
y=iris.target
target_names=iris.target_names
pca=PCA(n_components=2)
x_r=pca.fit(x).transform(x) #从这可以看出来pca是无监督学习
lda=LinearDiscriminantAnalysis(n_components=2)
x_r2=lda.fit(x,y).transform(x)
print(
"explained variance ratio (first two components): %s"
% str(pca.explained_variance_ratio_)
)
plt.figure()
colors=["navy",'turquoise','darkorange']
lw=2
for color ,i, target_name in zip(colors,[0,1,2],target_names):
plt.scatter(x_r[y==i,0],x_r[y==i,1],color=color,alpha=0.8,lw=lw,label=target_name)
plt.legend(loc="best",shadow=False,scatterpoints=1)
plt.title("PCA of IRIS dataset")
plt.figure()
for color,i,target_name in zip(colors,[0,1,2],target_names):
plt.scatter(x_r2[y == i, 0], x_r2[y == i, 1], color=color, alpha=0.8, lw=lw, label=target_name)
plt.legend(loc="best",shadow=False,scatterpoints=1)
plt.title("LDA of IRIS dataset")
plt.show()对比LDA和PCA,LDA是监督学习,PCA是无监督学习。
LDA:

PCA:

2.2 LDA和QDA分类的数学公式(Mathematical formulation of the LDA and QDA classifiers)
引入:
后验概率:
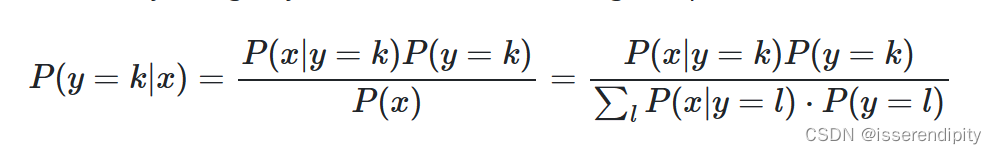
多元高斯分布:
QDA:
就是将后验概率求对数,预测类是使对数后验值最大化的类。
注:如果输入的每个类是独立的,QDA就相当于朴素贝叶斯分类器。
LDA:
LDA是QDA的一种特殊情况,它假设每个类的高斯函数共享相同的协方差矩阵。
这边的计算公式也特别复杂,大家可参考这个网站
3.核岭回归(Kernel Ridge Regression)
是Ridge Regression的kernel版本。
概念:
它在由各自的核和数据诱导的空间中学习线性函数。对于非线性核,这对应于原始空间中的非线性函数。
RR和KRR的比较:
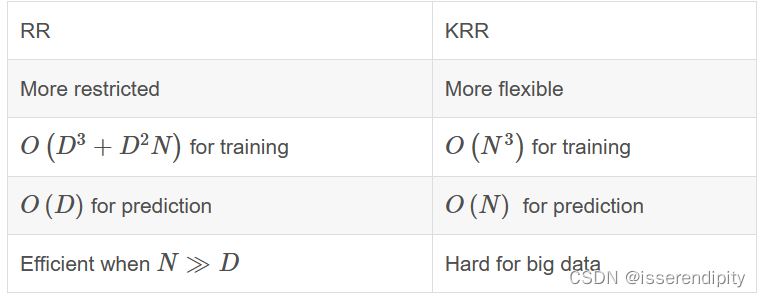
加入Kernal可以处理非线性数据,即,将数据映射到某一个核空间,使得数据在这个核空间上线性可分。