摘要

位操作（Bit Manipulation）是程序设计中对位模式或二进制数的一元和二元操作。在许多古老的微处理器上，位运算比加减运算略快，通常位运算比乘除法运算要快很多。在现代编程语言中，情况并非如此，很多编程语言的解释器都会基本的运算进行了优化，因此我们在实际开发中可以不必做一些编译器已经帮我们做好的优化，而就写出代码本身所要表现的意思。

在对位运算的学习过程中，可以锻炼写代码的思路，同时在面试过程中，如果使用位运算来对问题进行解决，也会很加分。

本篇文章从位运算的公式，再到一些比较经典的位运算题目进行讲解。从而帮助大家更好的掌握位运算。该文章下的所有题目都可以在leetcode中搜索到。学会了之后可以自己进行尝试。

1.位运算符

我们定义两个二进制数 A：1010（10） ，B：1101（15）

运算符	描述	结果
&	所有位按位进行与操作	A & B :1000
|	所有位按位进行或操作	A | B : 1111
>>	无符号右移	A >> 1 : 0100
<<	无符号左移	A<<1 : 10000
>>>	有符号右移	A >>> 1 : 0100
^	所有位按位进行异或操作	A ^ B : 0111
~	所有位按位进行取反操作	~A : 0101

2.>> 和 >>>的区别

现在说第一个问题，有符号右移和无符号右移有什么区别呢？
从上面的例子来看，似乎结果是一样的，为了解释这个问题，首先要解释一下在JS中，位运算的操作一共为32位，而第一位为符号位。

负数的二级制为对应正数的所有位取反加一

也就是说，对于2和-2来讲，他们的二进制为：

2： 00000000000000000000000000000010

-2：1111111111111111111111111111111111110

在针对负数进行操作的时候：

• 如果是无符号右移 >>，头部补1。所以就变成了：
  111111111111111111111111111111111111
  对应十进制的-1

• 如果是有符号右移 >>>，头部补0。就变成了：
  0111111111111111111111111111111111111
  对应十进制的2147483647
  所以使用>>>得到的一定是正数。

这里有一个比较常见的技巧：

<< 1 是×2的意思
>>1 是÷2的意思，但是位运算不能处理小数。
>>0 可以去掉小数点转换成整数

3.位运算公式

公式	结果
变为相反数 - x	~(x - 1) 或者 ~x + 1
x & -x	返回 x 的最后一位1
x >> k & 1	求 x 的第k位数字
x | (1 << k )	将 x 第k位数字置为1
x ^ (1 << k)	将 x 第k位数字取反
x & (x - 1)	将x最右边的1置为0(去掉最右边的1)
x | (x + 1)	将x最右边的0置为1
x & 1	判断奇偶性

上面的公式，最好能够自己通过一些例子进行演示出来。然后能做到碰到对应的情况下，直接想到。如果不能的话也要大概知道使用什么运算符，再自己进行推算出来。

因为后面要练习的题目，都要依靠于上面的公式技巧。所以这些公式还是需要掌握完全的，同时也要对位运算符的使用比较熟练。

4.经典题目

4.1 力扣67 二级制求和

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和。

输入:a = “11”, b = “1”
输出：“100”

输入：a = “1010”, b = “1011”
输出：“10101”

对于该题，很容易能想到的方法是，将字符串的二级制数转成十进制，然后进行相加，得到的结果再转成二进制。
但是这不是我们做这道题的初衷，我们可以通过模拟二进制加法的方式来对该题解答：

方法1：

从最低位进行相加，用一个变量来保存当前的进位（为0 或者 1）。
然后从后往前进行累加，并且通过配合当前进位来判断当前位置的值为0 还是 1

var addBinary = function(a, b) {
  let [num1,num2] = a.length > b.length ? [a, b] : [b, a]
  let result = '';
  let carry = 0
  for(let i = 0; i < num1.length;i++){
      let empty1 = num1[num1.length - i - 1];
      let empty2 = num2[num2.length - i - 1] || 0;
      if(+empty1 + +empty2 === 2){
          result = carry + result;
          carry = 1;
      }else if(+empty1 + +empty2 === 1){
          if(carry === 1){
              result = '0' + result;
          }else{
              result = '1' + result;
          }
      }else if(+empty1 + +empty2 === 0){
          result = carry + result;
          carry = 0;
      }
  }

    return carry? carry + result : result

};

当然这是我写的一个JS的版本，如果有更好的写法可以自己进行尝试。

方法2：

这道题可以通过将字符串转成十进制数。然后通过位运算实现加法的方式来解决。这里先不讲解该方法，在后面的位运算实现加减乘除里会对该方法进行实现。

4.2 力扣89 格雷编码

n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：

• 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
• 第一个整数是 0
• 一个整数在序列中出现 不超过一次
• 每对 相邻整数的二进制表示 恰好一位不同
• 且 第一个 和 最后一个 整数的二进制表示 恰好一位不同

给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

输入：n = 2 输出：[0,1,3,2] 解释： [0,1,3,2] 的二进制表示是 [00,01,11,10] 。

• 00 和 01 有一位不同
• 01 和 11 有一位不同
• 11 和 10 有一位不同
• 10 和 00 有一位不同 [0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
• 00 和 10 有一位不同
• 10 和 11 有一位不同
• 11 和 01 有一位不同
• 01 和 00 有一位不同

输入：n = 1 输出：[0,1]

方法1：

本题如果乍一看，似乎并不能通过逻辑的判断来进行解决。很容易就找不到思路，所以碰到这种情况，我们可以自己尝试着去列举，然后去发现其中的规律：

当n的值为1到3时，格雷编码的值应该为

• n = 1 : 0 1

• n = 2 : 00 01 11 10

• n = 3 : 000 001 011 010 110 111 101 100

从n = 1 到 n = 2 的转换过程，我们可以发现其中的规律，反转后首位+1

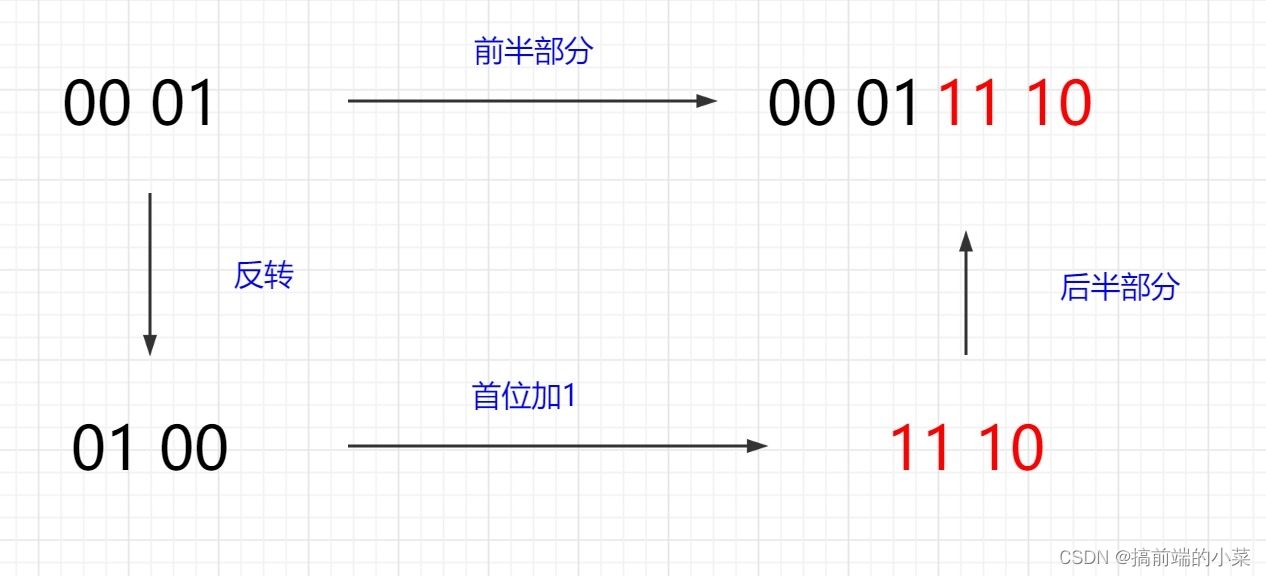
从n = 2 到 n = 3 的转换过程也遵循着这个规律

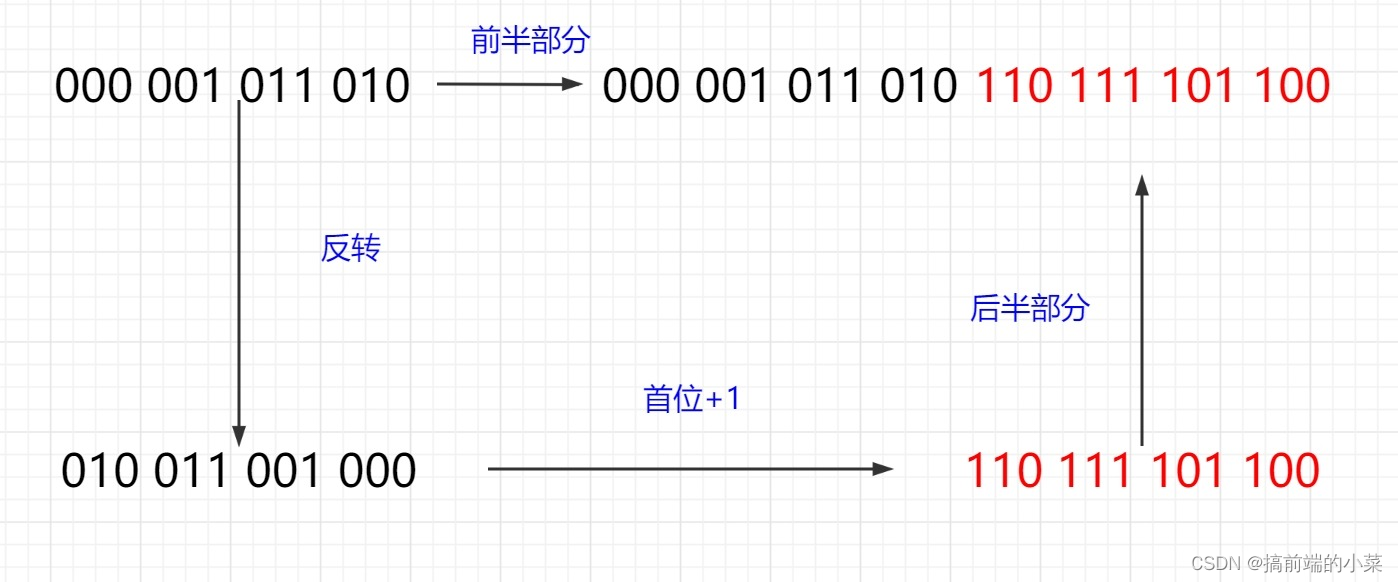
有了上面的规律，我们就可以编写代码了：

var grayCode = function(n) {
    let ret = [0,1];
    for(let i=0;i<n - 1;i++){
        let empty = []
        let reverseRet = [...ret].reverse();
        for(let j = 0 ; j< reverseRet.length;j++){
            empty.push(reverseRet[j] + (1 << (i+ 1)))
        }
        ret.push(...empty)
    }
  return ret;
};

方法二

如果有数字电路的基础，我们可以通过公式法来解决格雷编码的问题

公式：( i >> 1 ) ^ i
格雷编码的每一位为当前索引右移一位，异或本身

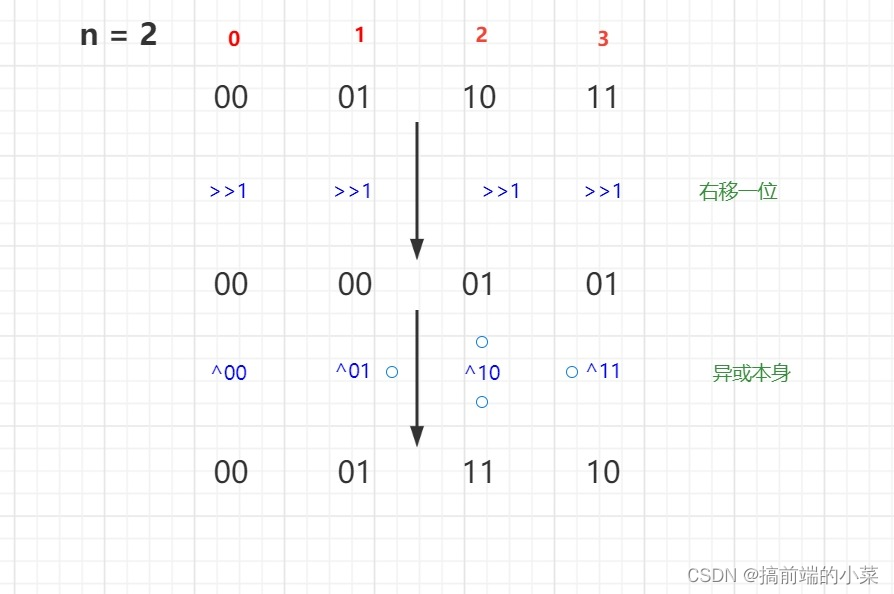
由上面的公式，我们很容易写出代码

var grayCode = function(n) {
  let ret = []
  for(let i = 0; i< 1 << n ; i ++){
      ret.push((i >> 1) ^ i)
  }
  return ret;
};

4.3 力扣136 只出现一次的数字

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

输入：nums = [2,2,1]
输出：1

输入：nums = [4,1,2,1,2]
输出：4

如果不考虑位运算，我们很容易想到通过双层for循环来进行判断每个数字是否只出现了一次。同时也可以考虑使用Map的方式来降低时间复杂度，不过会增加额外空间。

但是如果使用位运算，我们就可以在常量空间以线性复杂度的方法解决该问题。
这道题的重点在于

相同的数字异或为0：因为相同的数字每一位都是相同的，所以异或值都为0，结果自然为0。
0异或任何数等于数字本身：因为0异或1为1，0异或0为0，结果都为自身

所以我们可以通过对数组进行异或求和，最后的结果就是只出现了一次的数字（相同的数字都异或成了0）

var singleNumber = function(nums) {
  return nums.reduce((value1,value2) => value1 ^ value2);
};

4.4 力扣137 只出现一次的数字Ⅱ

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且不使用额外空间来解决此问题。

输入：nums = [2,2,3,2]
输出：3

输入：nums = [0,1,0,1,0,1,99]
输出：99

这道题同样可以使用遍历+Map的数据结构进行解答，但是会创造额外的空间。

和上一道题4.3不同，因为如果对该数组进行异或求和，出现三次的数字异或为自己本身（0 ^ 本身）。所以并不能通过异或的方式对该题进行求解。

这道题，我们要借助上面的公式
求 x 的第k位数字： x >> k & 1
将 x 第k位数字置为1：x | (1 << k )

现在我们来说一下解题思路，我们知道在JS中是32位二进制数。也就是说每个数字的二进制位都在32位以内。

对于所有的数字，不过是在这32位上有的为0，有的为1。
我们可以把0抽象成一个有32个位置的数组，而nums里的每个数的二级制都会往这个数组的不同位置放一个1，而出现三次的数字就会在这个数组上不同位置上放了三个1。

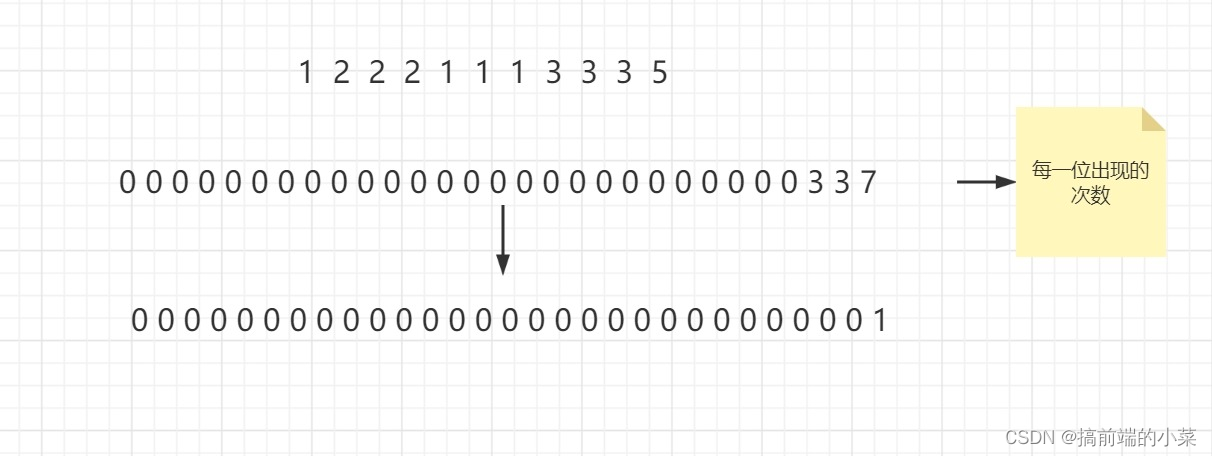
所以我们可以这样理解，对于这个32位的数组，每个位置的数字 k，如果k % 3 = 0（为3的倍数），就说明这个位置一定是0或者它是来自于那个出现三次的数字。反之，如果k % 3 != 0，就说明这个位置一定来自于出现一次的数字。

我们可以把k % 3 = 0的位置全部变成0，而k % 3 != 0的位置变成1，那么这个结果就是出现一次的数字。

所以根据这个思路，以及上面的两个公式，我们可以写出代码

var singleNumber = function(nums) {
  let result = 0;
  for(let i=0;i<32;i++){
      let sum = 0;
      for(let j=0;j<nums.length;j++){
          let empty = ( nums[j] >> i ) & 1;
          sum += empty;
      }
      if(sum % 3 !== 0){
          result |= (1 << i)
      }
  }
  return result
};

4.5 力扣260 只出现一次的数字Ⅲ

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案

输入：nums = [-1,0]
输出：[-1,0]

还是类似的题目，依旧可以通过遍历+Map的数据结构来进行解决。但是有了之前的经验，这道题想考我们的一定不是这个。

是否可以通过4.4题，通过判断每一位k是否为2的倍数的方式来解决问题呢？似乎不能，因为这两个不同的数字有可能在某一位都为1，从而打乱这个规律。
那是否可以通过4.1题，异或的方式来对该问题进行解决呢？可是如果对nums进行异或求和，得到的结果应该为 结果1 ^ 结果2

所以，如果我们有一种方法能够将结果1 ^ 结果2分开，从而得到正确的结果，这道题就迎刃而解了。

现在我们说解题思路，对于nums的异或求和，我们用K来代替，两个结果用num1和num2来代替。对于K来说，它为num1 ^ num2。
在K的二进制最后一位1，在相同的位置上，num1和num2一定是一个为1，一个为0。

而对于nums数组中的其他数字，在该位置上要么是0要么是1，而且都出现了两次，所以我们可以根据这个位置为0或者1，将数组分为两部分。第一部分为num1以及其他在该位置和num1相同的数字，并且它们都出现了两次，第二部分为num2以及其他在该位置和num2相同的数字，并且它们也都出现了两次。
我们对这两部分分别异或，得到的就是num1和num2。

所以这道题我们依赖的公式为
返回 x 的最后一位1：x & -x

根据上面的过程和公式我们可以得到代码：

var singleNumber = function(nums) {
  let res = 0;
  nums.forEach(element => {
    res ^= element;
  });

  let empty = res & -res;

  let left = 0,right = 0;
  nums.forEach(element => {
    if(element & empty){
      left ^= element
    }else{
      right ^= element
    }
  })
  return [left,right]
};

4.6 力扣190 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111

如果前面的习题都已经掌握，对于这一道题来说，就已经不算困难了。
我们只需要每次拿到 n 的最后一位 k（公式在上面），然后依次排开就是我们最后的结果。
怎么按顺序排开每次拿到的最后一位数字 k 呢？只需要将 k 对应左移（例如第一次拿到的k就要左移32位），然后和0进行或运算。最终就可以得到我们想要的结果。

这里面需要注意的是，在JS中，是具有符号位的，所以在进行右移的时候，要使用>>>进行有符号位移。而最后的结果需要通过 >>> 0 转换位无符号整数。而在JS中只能通过>>>0转换成无符号整数。

var reverseBits = function(n) {
    let result = 0;
    for(let i=0;i<32 && n > 0;i++){
        result |= (n & 1) << (31 - i);
        n = n >>> 1
    }
    return result >>> 0
};

4.7 力扣191 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。

哇，这道题如果对上面的公式已经掌握，直接就是手到擒来。我们可以每次都将 n 的最后一位1变成0（公式法），记录1的出现次数，直到 n 的值变成了0，也就是最后我们想要的结果了。

var hammingWeight = function(n) {
    let res = 0;
    while(n != 0){
        n = n & (n - 1);
        res ++
    }
    return res;
};

4.8 力扣201 数字范围按位与

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）。

输入：left = 5, right = 7
输出：4

输入：left = 0, right = 0
输出：0

输入：left = 1, right = 2147483647
输出：0

这道题光看题目来讲，似乎直接从left直接与到right就能得到答案，但是作为力扣的一道中等题。一定不是想这么考察我们的。而且即便这么写，在力扣中例三也无法通过编译。

所以我们要找到能降低时间复杂度的方法，我们先把例子列出来看一下是否能通过过程，来找到一些规律。

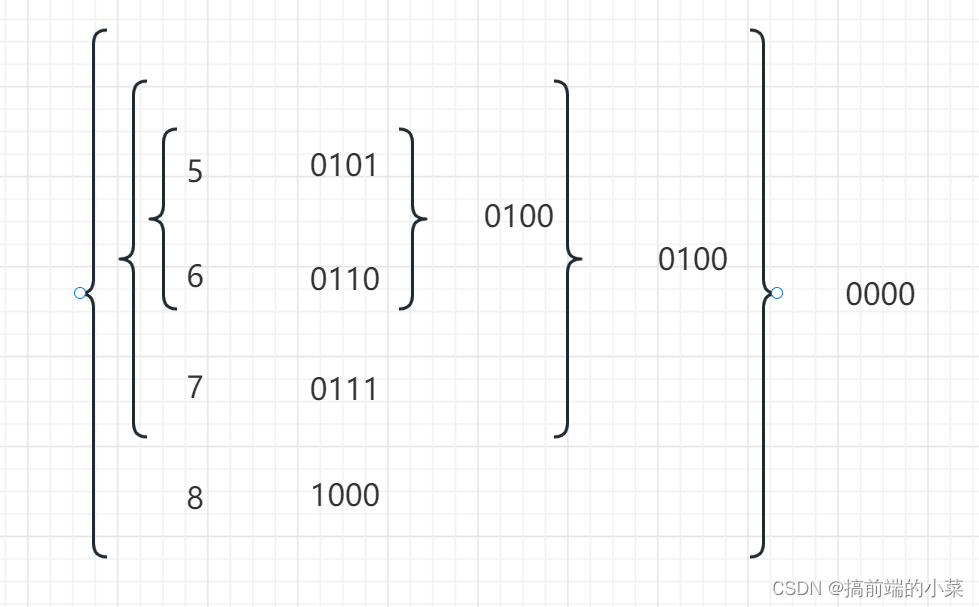
从上面的图我们可以发现，似乎 left 一直到 right 与操作的结果，是left和right公共的前部分，然后后面全部补0.

大家也可以多举一些例子，验证一下这个方案。其实原理就是，从right向左进行与操作，其实就是一直在将末尾的1变成0。所得到的值只要比left大，那么一定是可以继续操作的。但如果一旦比left小，那么这个值一定是最后的结果。

var rangeBitwiseAnd = function(left, right) {
    while(left < right){
        right = right & (right - 1)
    }
    return right
};

4.9 力扣231 2的幂

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

输入：n = 1
输出：true
解释：20 = 1

输入：n = 16
输出：true
解释：24 = 16

首先我们要知道，满足2的幂的数字，它二进制位是只有一位1的。
在公式里面 x & (x - 1) 是将二进制位的最后一位1置为0。如果x的二进制位只有一个1，那么x & (x - 1) 之后的数字，一定是0。我们就可以通过这个方法来进行判断，数字是否为2的幂。

var isPowerOfTwo = function(n) {
    return n > 0 && n !== 0 && (n & (n - 1)) === 0;
};