1.题目

观察这个数列：

1 3 0 2 -1 1 -2 …

这个数列中后一项总是比前一项增加2或者减少3，且每一项都为整数。

栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加 a 或者减少 b 的整数数列可能有多少种呢？

输入格式
共一行，包含四个整数 n,s,a,b，含义如前面所述。

输出格式
共一行，包含一个整数，表示满足条件的方案数。

由于这个数很大，请输出方案数除以 100000007 的余数。

数据范围
$1\le n\le 1000,$
$-10^9\le s\le 10^9,$
$1\le a,b\le 10^6$

输入样例：

4 10 2 3

输出样例：

2

样例解释

两个满足条件的数列分别是2 4 1 3和7 4 1 -2。

2.基本思想

DP

分析

设第一个数为$x$，则第二个数为$x+d1$，第三个数为$x+d1+d2\dots$，（这里的$d1，d2$表示$a$或者$-b$，）则长度为n的

序列所有的项为：

$x,x+d1,x+d1+d2,x+d1+d2+d3,\dots ,x+d1+d2+\dots +dn-1$，又因为数列之和为s，所以转化成：

$n\ast x+(n-1)\ast d1+(n-2)\ast d2+(n-3)\ast d3+\dots +dn-1=s$，再在一步转化：

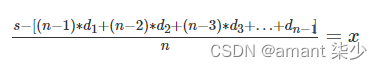
因为x是任意整数，所以 $(s-((n-1)d1+(n-2)d2+(n-3)d3+\dots +dn-1))$一定为 0 ，

因此推出$s$，

也就是两者的模$n$的余数必须相同；

$s$是确定的，即最后就是要求$(n-1)d1+(n-2)d2+(n-3)d3+\dots +dn-1$这个式子的所有可能的和模$n$的余数是$s$的结果数

到这里就转化成了组合问题。

动态规划
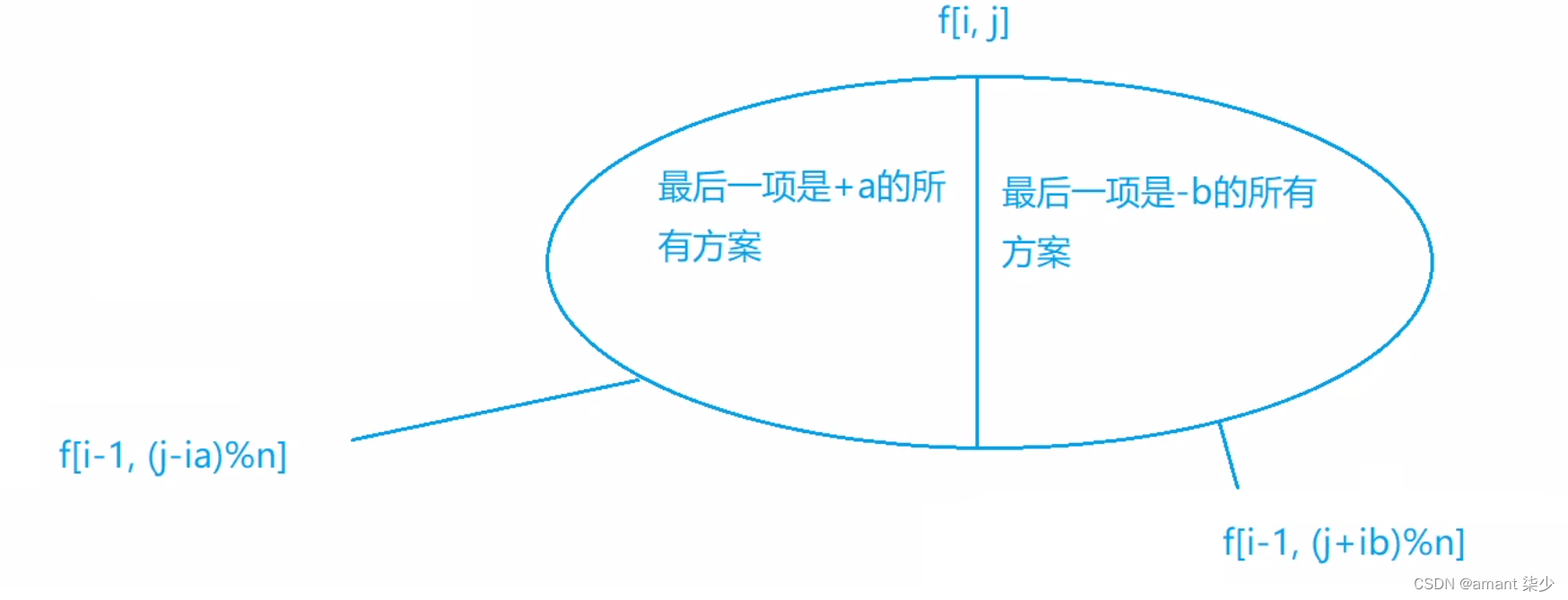
1.状态表示:

1.1集合：$f[i][j]$:所有只考虑前i项取(a或-b)且当前i个数的总和除以$n$的余数是$j$的方案的集合的数量
1.2属性：count

2.状态计算

递推关系：第i个可以选a或者-b。
第i个选a，则前i个数的和为：
$[(n-1)d1+(n-2)d2+\dots +(n-(i-1))di-1+(n-i)a]$%n≡j%n
$(n-1)d1+(n-2)d2+\dots +(n-(i-1))di-1\equiv j-(n-i)a$
因为$f[i][j]$代表的是组合数量，因为$j-(n-i)a$是已经确定的数值，所以变化的数量在前面的和里面，可以推出
所以$f[i][j]=f[i-1][j-a(n-i)]$
同理，如果选$-b,f[i][j]=f[i-1][j+b(n-i)]$
$f[i][j]=f[i-1][j+b(n-i)]+f[i-1][j-a(n-i)]$

3.代码实现

import java.util.Scanner;

public class _1214波动数列 {
    static Scanner sc = new Scanner(System.in);
    static int MOD = 100000007;
    static int dp[][] = new int[1010][1010];

    public static void main(String[] args) {
        int n = sc.nextInt();
        int s = sc.nextInt();
        int a = sc.nextInt();
        int b = sc.nextInt();

        //初始化
        dp[0][0] = 1;
        
        for (int i = 1; i <= n; i++)//枚举所有状态
            for (int j = 0; j < n; j++)//枚举余数
                dp[i][j] = (dp[i - 1][get_mod(j-(n-i)*a,n)] + dp[i - 1][get_mod(j+(n-i)*b,n)]) % MOD;
        System.out.println(dp[n - 1][s % n]);
    }

    static int get_mod(int a, int b) {//求 a除以b的正余数
        return (a % b + b) % b;
    }
}