通信原理(1)–信息的度量，通信系统的性能指标

1.1通信的基本概念

• 消息、信息与信号
• 通信系统的组成模型
• 数字通信的特点
• 通信系统的分类
• 通信的方式

1.1.1通信的发展

1.1.2消息、信息与信号

• 消息的定义

消息是通信系统要传输的对象，包含连续消息和离散消息。连续消息：语音、温度、活动图片等；
离散消息：计算机数据、符号、文本等。

• 信号的定义

信号是消息的电表示形式，为消息的物质/传输载体。
模拟信号：信号参量取值连续的信号；
数字信号：信号参量取值离散的信号。

• 信息的定义

消息中蕴含的内容，原来未知而待知的内容。

• 消息，信息和信号的关系

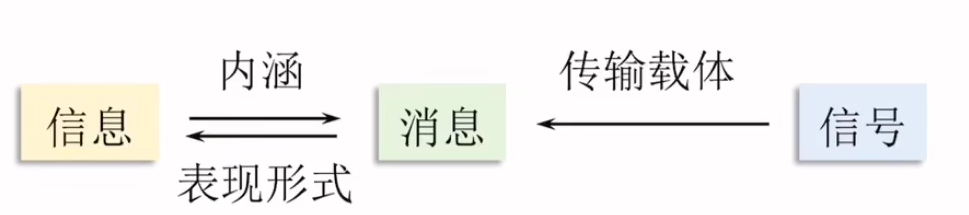
1. 信号是消息的传输载体
2. 消息是信息的表现形式
3. 信息是消息的内涵

• 通信的目标

利用电信号传输消息中包含的信息，收端获得信息后，不确定性被消除。

1.2通信系统模型

1.2.1通信系统一般模型

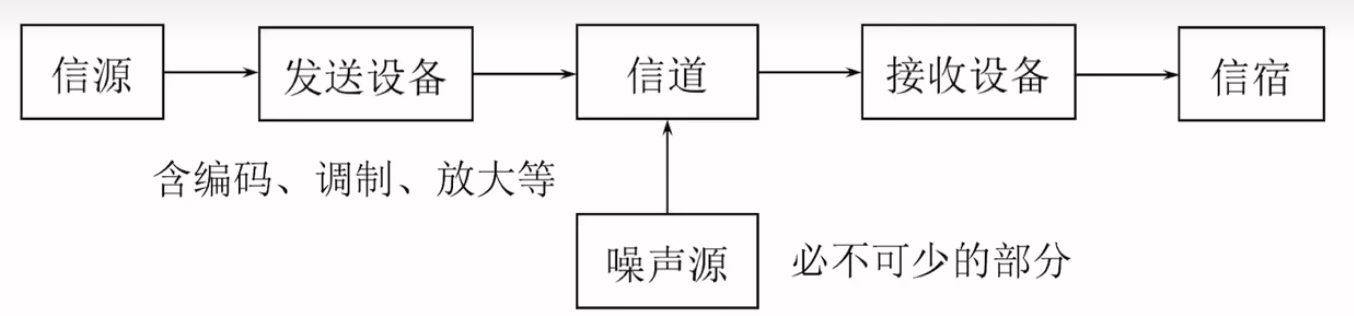
信源：将消息转化为电信号发出

发送设备：将原始的电信号转化为适合在信道中传输的信号

信道：能够传输信号的各种物理媒介

接收设备：与发送设备功能互逆，可能包含解调、译码等

信宿：将电信号转化为消息，收到信息

1.2.2模拟通信系统模型

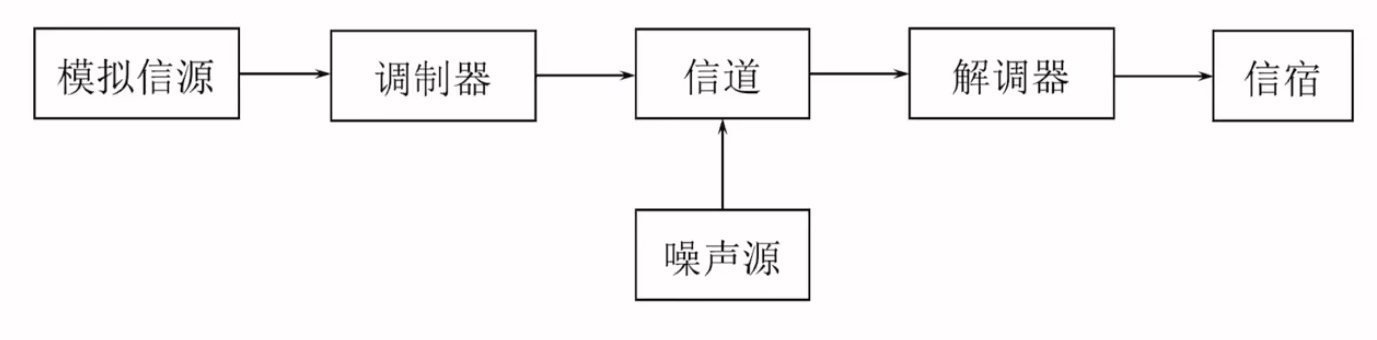
模拟电信号转化为原始电信号（基带信号）后，通过调制转化为已调信号（带通信号），传送的是模拟波形。
调制是为了让信号更适合在信道中传输，解调是调制的逆过程。

1.2.3数字通信系统模型

信源编码：A/D转换，通过数据压缩去冗余，提高通信系统有效性

信道编码：提高系统抗干扰能力，通过加冗余提高通信系统的可靠性

数字调制：把信息加到高频载波上

数字解调：从已调信号中卸载信息

1.2.4数字通信的特点

优点：

• 抗干扰能力强，噪声不积累；数字通信看状态，模拟通信看保真度
• 传输差错可控：==便于处理、变换、存储；
• 便于将来自不同信源的信号综合传输；
• 易于集成，便于加密。

缺点：

• 需要较大的传输带宽；
• 对同步要求高，设备复杂

1.3通信系统分类与通信方式（大概了解）

1.3.1通信系统的分类（大概了解）

• 按信道信号特征分类

模拟通信、数字通信

• 按传输媒质分类

有线通信、无线通信

• 按传输方式分类

基带传输、带通传输

• 按通信业务分类

电话、数据、视频、图像通信等

• 按工作波段分类

长波、中波、短波、微波、红外以及激光通信等

• 按复用方式分类

频分、时分、码分、空分、波分复用等

同一个通信系统可分属于不同的分类。如AM广播系统属于中、短波通信系统，模拟通信系统以及带通传输系统。

1.3.2通信方式（大概了解）

1.3.2.4 按传输方向和时间划分

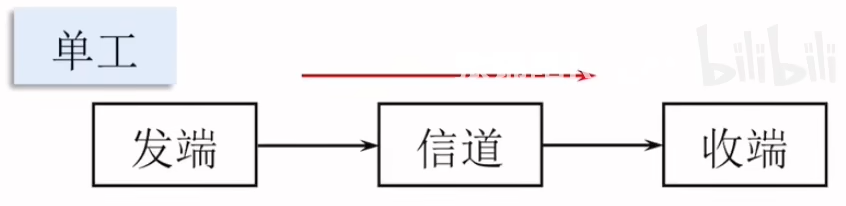
单工通信

发端单向传输至收端。
例：广播通信。

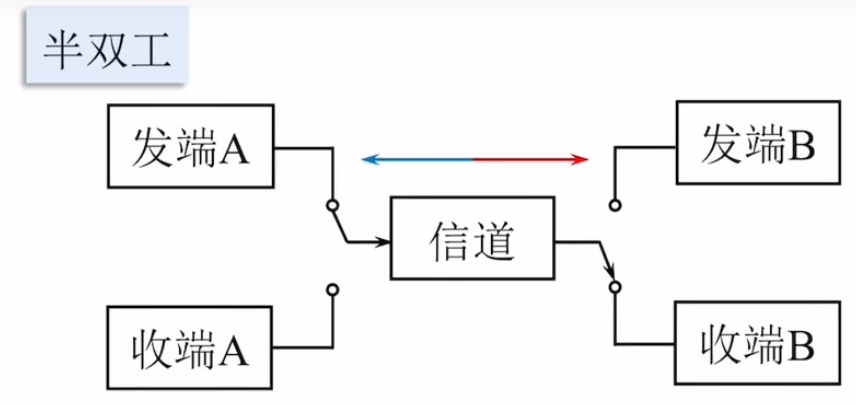
半双工通信

收发可双向传输，但不能同时传输。例：对讲机。

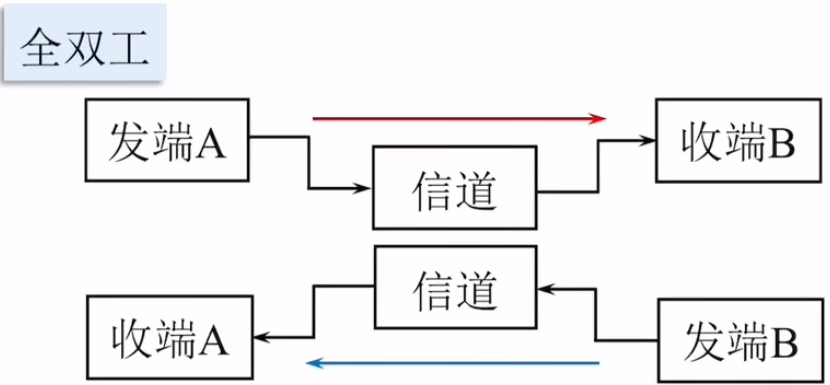
全双工通信

收发可双向传输，也可以同时传输。例：电话。

1.3.2.2 按码元传输时序划分

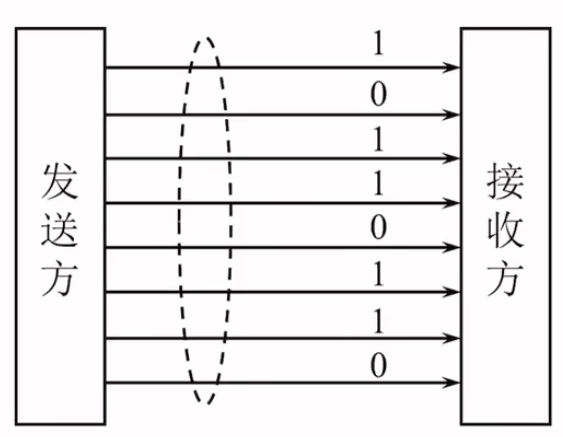
• 并行传输

在并行信道上同时传输n个bit信息。

优点：节省传输时间，速度快；
缺点：需要n条通信线路，成本高；

应用：设备之间近距离通信，如计算机、打印机。

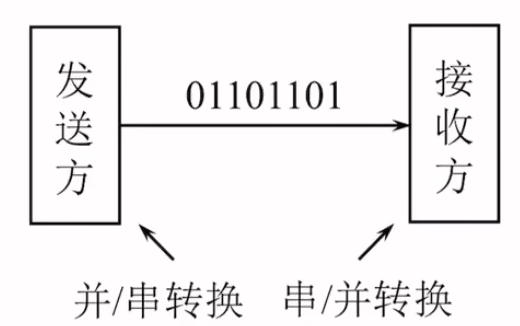
• 串行传输

数字码元序列按时间顺序一个接一个地在一条信道中传输。

优点：只需要1条通信线路，成本低；

缺点：速度慢，需要外加同步措施；

应用：远距离通信。

1.4信息及其度量

通信的本质是传递信息，为了定量表征信息的度量，引入自信息量的概念。事件包含的信息量是事件发生概率的函数，即：
$$I(x_i)=f\left[\begin{array}{c}P(x_i)\end{array}\right]$$
需满足的四个性质

$$P(x_1)>P(x_2)\Rightarrow I(x_1)<I(x_2)$$
$$P(x_i)=0\Rightarrow I(x_i)=\infty$$
$$P(x_i)=1\Rightarrow I(x_i)=0$$
$$独立可加性：I(x_i{y}_i)=I(x_i)+I(y_j)$$

• 概率越大，信息量越小
• “通信原理不好学”概率越小，信息量越大
• “买彩票中头奖”确定事件，信息量为0。“太阳东升西落”

1.4.1离散消息的信息量

自信息定义
$$I(x_i)={\log }_a\frac{1}{P(x_i)}=-{\log }_{a}P(x_i)$$
自信息是物 理量，有单位，取决于对数运算的底数a

• 以2为底，单位为比特/bit（binaryunit）；
• 以e为底，单位为奈特/nat（naturalunit）；
• 以10为底，单位为哈特/hat（Hartleyunit）；
• 以M为底，单位为M进制单位。

实际中常采用以2为底的对数，即以bit作为自信息量的单位。

ps:如果不会算10为底的对数可以通过换底公式转换为2为底的公式。
$$lg(x)=\frac{lo{g}_2(x)}{lo{g}_2(10)}$$

$$lo{g}_2(x)=lg(x)lo{g}_2(10)=\frac{lg(x)}{lg(2)}\approx 3.322\cdot lg(x)$$

自信息量的物理意义

• 在事件发生前：描述事件发生不确定性的大小；
• 在事件发生后：表示该事件所含有（提供）的信息量；
• 在理想信道中：等于收信者接收到该消息后所获取的信息量，意味着不确定度的消除。

离散信源的平均信息量一—信息熵

信源熵定义

对于离散信源，含有M个可能的取值，其概率空间为：
$$\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_M\\ P(x_1)& P(x_2)& \cdots & P(x_M)\end{array}\right]0\le P(x_i)\le 1,\sum _{i=1}^{M}P(x_i)=1$$
信源平均自信息量（熵）定义为信源中每个符号所含信息量$I(x_i)$的统计平均值
$$H=E\left[I(x_i)\right]=\sum _{i=1}^{M}P(x_i)I(x_i)=\sum _{i=1}^{M}P(x_i)\log \frac{1}{P(x_i)}$$
单位为：bit/符号

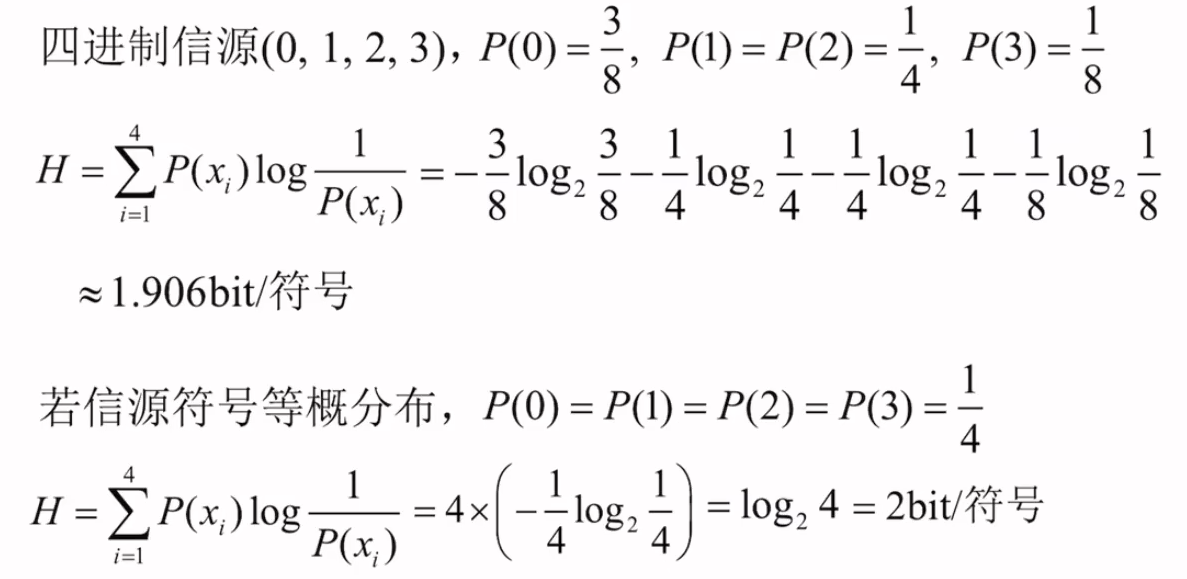
此时便可以得到一个结论：等概的时候熵最大。

结论

信源内符号等概分布时，信息的熵最大。
$$H_{\max }={\log }_{2}M$$
对于m个统计独立的符号构成的消息，总的信息可近似计算为：
$$I_{\text{总}}=m\cdot H$$
平均自信息表征信源的整体特性，定义整个信源的不确定度，又称为：信息熵/信源熵/香农熵/无条件熵/熵函数等，简称为痛。

1.5通信系统主要性能指标

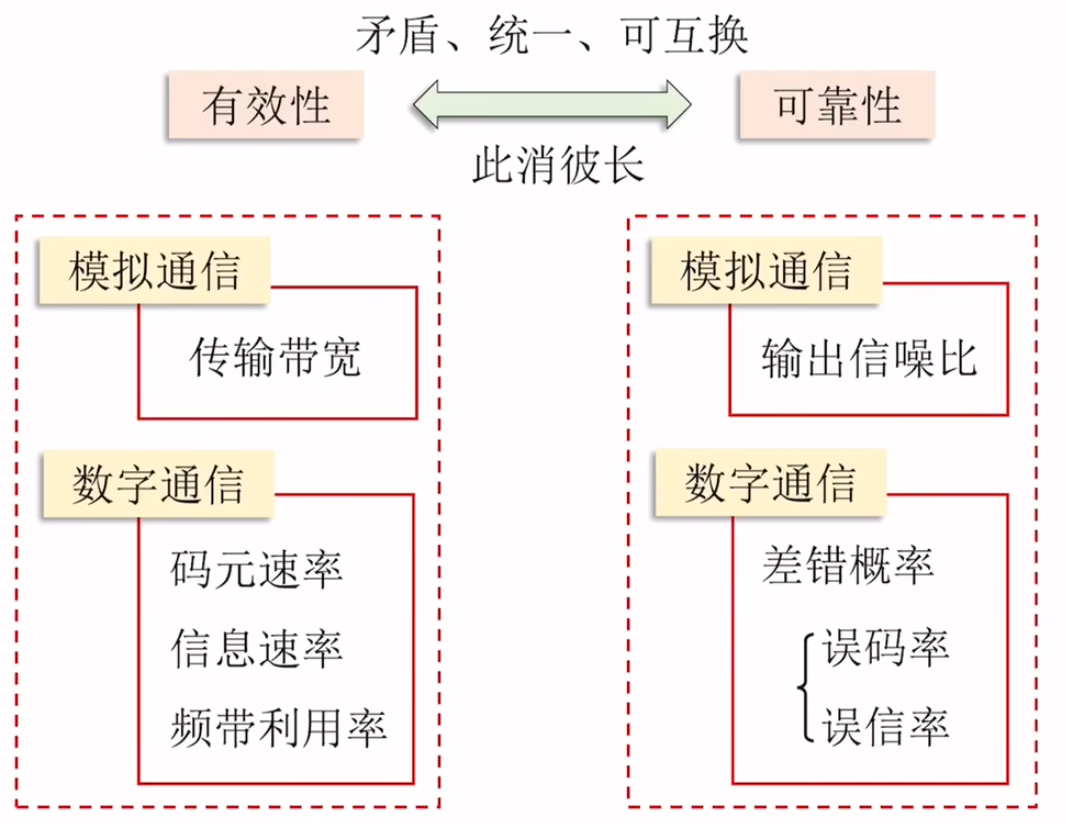
1.5.1有效性

码元传输速率$R_b$:传码率、符号率、波特率

定义:码元传输速率定义为每秒传送的码元个数。

单位:波特（Baud，简写为B），符号/s。

计算:若每个码元时间长度为$T_B$，则
$$R_B=\frac{1}{T_B}$$
符号率与进制数无关，与信源统计特性无关。

信息传输速率$R_b$:传信率、比特率

定义:每秒传送的bit数、即信息量，或每秒传递的二进制码元个数。

单位:bit/s，简记为b/s或bps。

$R_b$和$R_B$的关系

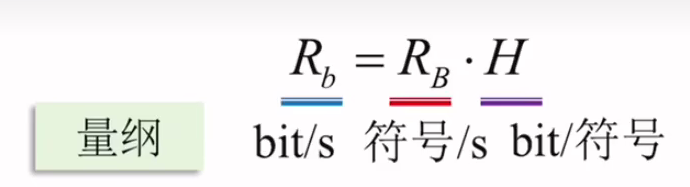
常用等概时的情形，若M个符号等概分布，此时：
$$R_b=R_B\cdot {\log }_{2}M$$
二进制时，M=2，$R_b$=$R_B$，符号率和比特率数值相等，但单位不等。

频带利用率

将带宽与传输速率相结合

定义:单位带宽内的传输速率。
$$\{\begin{array}{ll}\eta =\frac{R_B}{B}& \text{(Baud/Hz)}\\ & \\ {\eta }_b=\frac{R_b}{B}& \text{(bit/s}\cdot {\text{Hz}}^{-1})\end{array}$$
${\eta }_b=\eta {\log }_{2}M{\eta }_b$的单位也可也记为$b/(s\cdot Hz)或bps/Hz$

1.5.2可靠性

误码率$P_e$（误符号率）

$$P_e=\frac{\text{错误码元数}}{\text{传输总码元数}}=\frac{N_e}{N}$$

误信率$P_b$（误比特率）

$$P_b=\frac{\text{错误比特数}}{\text{传输总比特数}}=\frac{I_e}{I}$$

$\text{二进制时:}{P}_e=P_b\text{多进制(}M>2\text{)时:}{P}_e>P_b$