week35 SE-LSTM

摘要

本周阅读了题为Large-scale water quality prediction with integrated deep neural network的论文。这项工作提出了一种基于长期短期记忆的编码器-解码器神经网络和 Savitzky-Golay 滤波器的混合模型。其中，Savitzky-Golay滤波器可以消除水质时间序列中的潜在噪声，长短期记忆可以研究复杂水环境中的非线性特性。这样就提出了一个集成模型并有效地获得了统计特征。基于真实数据的实验证明，其预测性能优于几个最先进的同行。

Abstract

This week read the paper entitled Large-scale water quality prediction with integrated deep neural network. This work proposes a hybrid model based on a long short-term memory-based encoder-decoder neural network and a Savitzky-Golay filter. Among them, the filter of Savitzky-Golay can eliminate the potential noise in the time series of water quality, and the long short-term memory can investigate nonlinear characteristics in a complicated water environment. In this way, an integrated model is proposed and effectively obtains statistical characteristics. Realistic data-based experiments prove that its prediction performance is better than its several state-of-the-art peers.

一、文献阅读

1. 题目

标题：Large-scale water quality prediction with integrated deep neural network

作者：Jing Bi, Yongze Lin, Quanxi Dong, Haitao Yuan, MengChu Zhou

期刊名：Information Science

链接：https://doi.org/10.1016/j.ins.2021.04.057

2. abstract

这项工作提出了一种基于长期短期记忆的编码器-解码器神经网络和 Savitzky-Golay 滤波器的混合模型。其中，Savitzky-Golay滤波器可以消除水质时间序列中的潜在噪声，长短期记忆可以研究复杂水环境中的非线性特性。这样就提出了一个集成模型并有效地获得了统计特征。基于真实数据的实验证明，其预测性能优于几个最先进的同行。

This work proposes a hybrid model based on a long short-term memory-based encoder-decoder neural network and a Savitzky-Golay filter. Among them, the filter of Savitzky-Golay can eliminate the potential noise in the time series of water quality, and the long short-term memory can investigate nonlinear characteristics in a complicated water environment. In this way, an integrated model is proposed and effectively obtains statistical characteristics. Realistic data-based experiments prove that its prediction performance is better than its several state-of-the-art peers.

3. 网络架构

该文提出的模型改进了编码器-解码器网络结构，使其能够更好地适应多步时间序列预测。同时，为了解决时间序列数据的降噪问题，该工作采用SG滤波器对原始数据进行去噪。G 滤波器可以有效保留时间序列的特征，并去除其噪声。同时，结合基于LSTM的编码器-解码器模型，模型显着提高了多步预测的准确性。

3.1 Savitsky-Golay 滤波器

·

3.2 模型结构——SE-LSTM

该模型提出了混合框架，该框架通过结合SG滤波器和基于LSTM的编码器-解码器网络来实现对未来水质的预测

问题表述： X = { x 1 , . . . , x t , . . . , x T } X=\{x_1,...,x_t,...,x_T\} X={x1​,...,xt​,...,xT​}表示水质的时间序列，T表示之前的T个时间步长。 $\overline{x}$表示SG过滤器处理后的水质值。 $\hat{y}$表示水质值的预测序列。 Y ^ = { y ^ 1 , . . . , y ^ t ′ , . . . , y ^ τ } \hat Y=\{\hat y_1,...,\hat y_{t'},...,\hat y_\tau\} Y^={y^​1​,...,y^​t′​,...,y^​τ​} 代表接下来s个时间步的预测值。

降噪后，本工作采用LSTM模型来预测水质。 LSTM 可以从重要的经验中学习，这些经验具有长期的依赖关系。 LSTM的存储单元如下图所示。

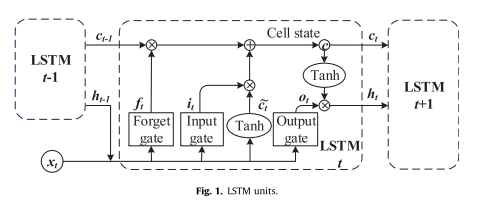
LSTM的反向传播（BP）算法与RNN的算法一致。

为了获得更好的预测精度，这项工作提出了一种新颖的编码器-解码器神经网络，如下图所示。

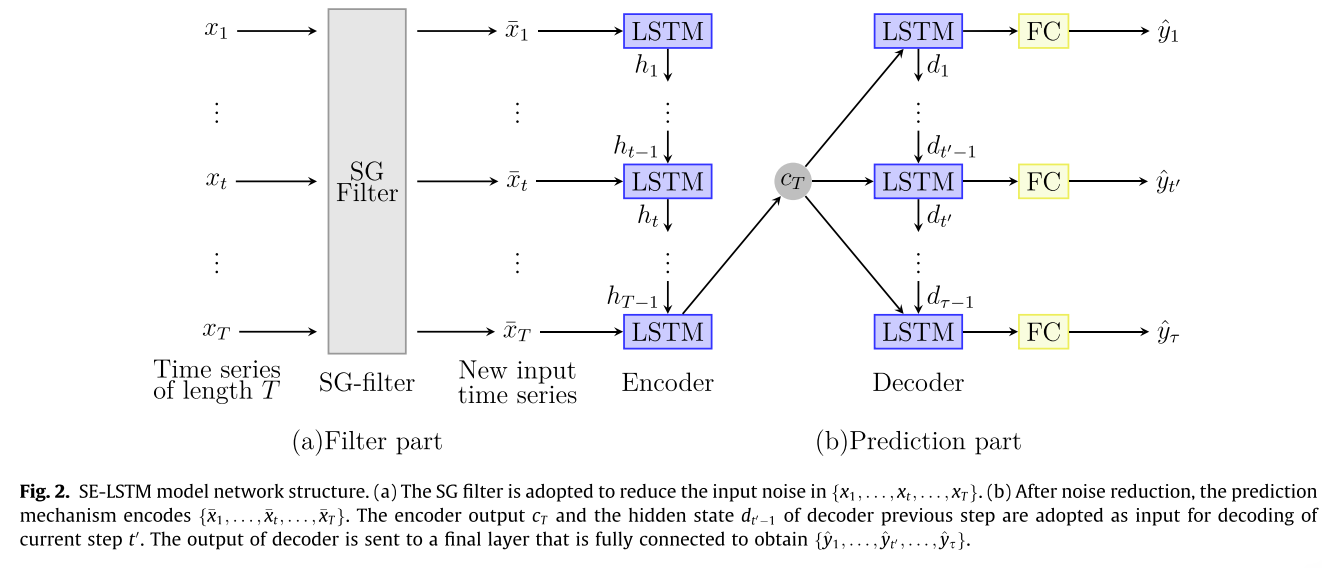
上图中的编码器网络是一个LSTM，它对输入 { x 1 , . . . , x t , . . . , x T } \{x_1,...,x_t,...,x_T\} {x1​,...,xt​,...,xT​}进行顺序变换；。然后，获得 t 处从 $x_t$ 到 $h_t$ 的映射：
$$h_t=f_1(h_{t-1,x_t})\text{\hspace{1em}(12)}$$
其中 $h_t$ 是编码器在 t 时的隐藏状态，$f_1$ 是 LSTM 的一个单元。

$c_T$是基于LSTM的编码器获得的隐藏状态信息。解码器也是一个LSTM，通过获取 { y ^ t , . . . , y ^ t ′ , . . . , y ^ τ } \{\hat y_t,...,\hat y_{t'},...,\hat y_{\tau}\} {y^​t​,...,y^​t′​,...,y^​τ​}来产生输出给定隐藏状态$d_{t^{\prime }}$，而 $d_{t^{\prime }}$以 $c_T$ 为条件。令 $d_{t^{\prime }}$ 表示解码器在 $t^{\prime }$ 时的隐藏状态信息。因此，$d_{t^{\prime }}$​ 可得为：
$$d_{t^{\prime }}=f_2(d_{t^{\prime }-1},c_T)\text{\hspace{1em}(13)}$$
$f_2$ 是另一个 LSTM 单元。 LSTM 提取时间序列的复杂特征。在多步预测中，编码器的输出$c_T$和来自解码器的隐藏状态$d_{t^{\prime }-1}$​的最后一步可以提高多步预测的性能。全连接层可以将它们输出为预测值，如下所示。
$${\hat{y}}_{t^{\prime }}=w_k^T\cdot d_{t^{\prime }}\text{\hspace{1em}(14)}$$
模型步骤

1. SG滤波器
   • 将原始序列 { x 1 , . . . , x t , . . . , x t } → { x ‾ 1 , . . . , x ‾ t , . . . , x ‾ T } \{x_1,...,x_t,...,x_t\}\rightarrow \{\overline x_1,...,\overline x_t,..., \overline x_T\} {x1​,...,xt​,...,xt​}→{x1​,...,xt​,...,xT​}
2. 基于LSTM的编码器层
   • $h_t=f_1(h_{t-1},x_t)$，$h_t$是t时刻编码层的隐藏状态，$f_1$是一个LSTM单元<得到从$x_t$到$h_t$的映射>
3. 基于LSTM的解码曾
   • $d_{t^{\prime }}=f_2(d_{t^{\prime }-1},c_T)$，$c_T$是由编码器得到的隐藏状态信息，$f_2$是一个LSTM单元，$d_{t^{\prime }}$​是解码在t’时刻的隐藏状态信息
4. 全连接层
   • ${\hat{y}}_{t^{\prime }}=W_k^T\cdot d_{t^{\prime }}$，W为权重，k为层数，${\hat{y}}_{t^{\prime }}$​为t’处的预测值

4. 文献解读

4.1 Introduction

水质的精确预测有助于水环境的管理。传统的神经网络无法捕获长期依赖性。长期依赖性意味着期望的输出取决于很久以前出现的输入。为了解决这一挑战，研究人员提出了一种长短期记忆（LSTM）模型，该模型采用记忆机制来捕获长期依赖性，并普遍应用于不同类型的现实生活领域。然而，由于数据中的噪声，这些预测模型经常遇到过度拟合的问题。 Savitzky-Golay（SG）滤波器可以减少时间序列的噪声干扰，提高上述模型的预测精度。

4.2 创新点

这项工作设计了一种混合模型，使用基于 LSTM 和 SG 滤波器的编码器-解码器神经网络（称为 SELSTM）来预测未来的水质。主要贡献总结如下：

1. 提出了一种改进的编码器-解码器网络结构，可以更好地预测多步水质时间序列数据。因此，所提出的SE-LSTM可以更好地处理时间序列数据中的长序列。
2. 创新性地将SG滤波器的降噪能力和LSTM的特征提取能力结合和集成，显着提高了多步预测精度。

4.3 实验过程

4.3.1 训练参数

采用MAE作为SE-LSTM的损失函数，SE-LSTM采用Adam优化器[28]中的梯度下降算法。这里，为了有效地训练模型，初始学习率设置为0.01，使用$1\times 10^{-6}$作为训练损失衰减

4.3.2 数据集

实验数据集采集自北京古北口，该数据每4小时收集一次，从2014年4月到2018年10月共收集了1万多条数据。然后将数据集分成两部分，包括训练集和测试集，比例为9:1。所有预测模型均采用溶解氧(DO)和化学需氧量(CODMn)作为实验数据。DO和CODMn的分布如图所示：

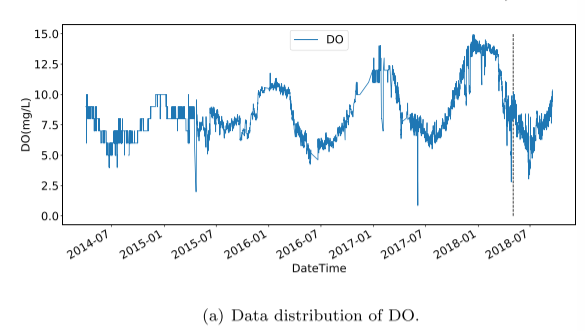
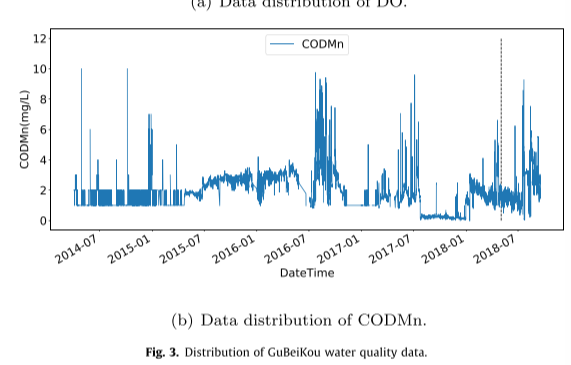
4.3.3 实验设置

在数据预处理中，本工作采用平滑操作来消除不稳定因素，但同时也去除了原始时间序列中的一些有效信息。首先在对比实验中通过不同的窗口尺寸选择出最佳的过滤器，在原始时间序列的移动中值(MM)、SG和MA滤波器中，当窗口大小为5时三个过滤器获得最小的MSE值，并且SG滤波器的MSE值最小。

在设置SG滤波器参数中，我们给出了不同的参数设置，当窗口大小为5，即m¼5，并且k度的多项式设置为3时，获得的均方根误差(RMSE)较小。过大的窗口尺寸会去除时间特征，而过小的窗口尺寸则不能用于降噪。同样，k太大会导致最小二乘过拟合，k太小会导致欠拟合。

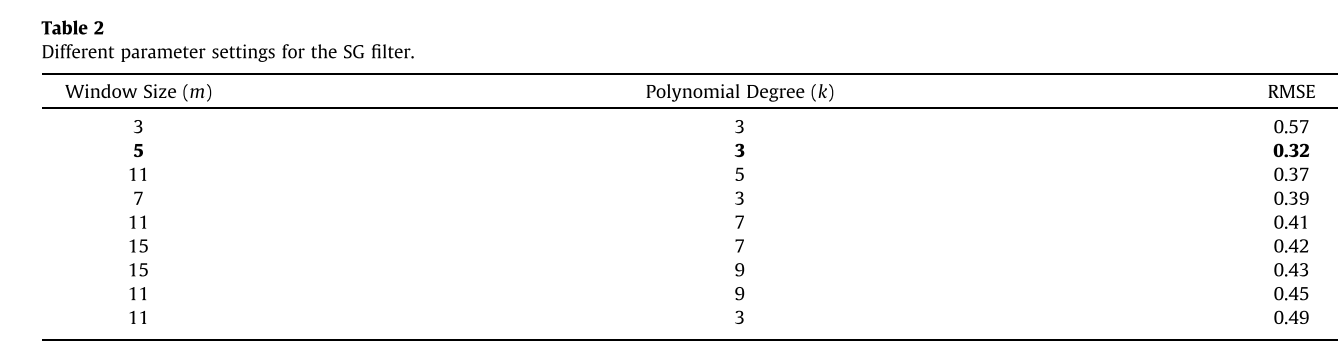
评估指标：为了证明SE-LSTM的预测性能，采用MAE、MAPE和RMSE三个指标来评价其预测精度。

基准模型：

为了从不同方面比较所提出的方法，我们选择了几个基准模型进行比较。

ARIMA。将过去值和随机噪声通过线性函数拟合到预测值中。
ANN。人工神经网络能很好地处理非线性特征，并具有良好的预测能力。
极端梯度增强(XGBoost)。是一种通用的Tree Boosting算法，它被广泛应用于机器学习领域。首先利用树集成技术构建回归树，并将所有回归树的总得分作为最终预测值。
SVR。SVR可以通过获得最小的结构风险来提高泛化能力，在统计样本较少的情况下，也能得到较好的统计规律。
LSTM。LSTM是一种常用的序列预测模型，特别是LSTM在产生时间序列的长期依赖关系方面表现优异。为了比较LSTM和SE-LSTM的性能，实验中它们的超参数设置相同。

4.3.4 实验结果

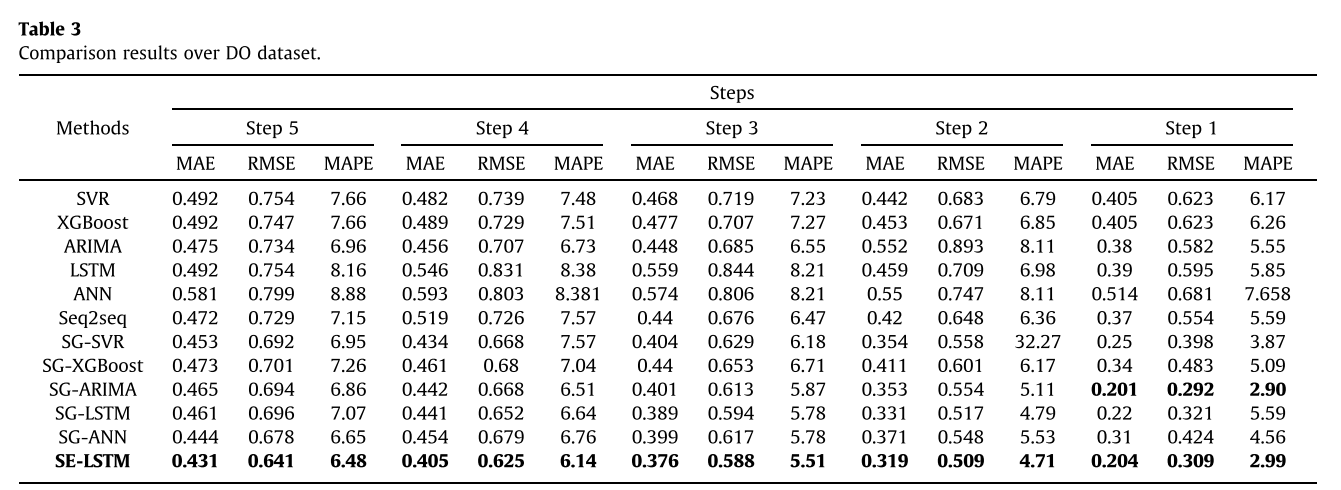
将SE-LSTM与其典型的基准测试方法进行比较，实验结果表明，传统的非线性模型与线性模型相比并没有太大的优势。这是因为水质时间序列具有较强的线性特征，线性模型具有一定的优势。此外，深度学习的预测精度优于传统模型，并且由于网络结构的变化，SE-LSTM在多步预测精度上优于SG-LSTM。此外，在加入SG滤波器后，所有模型的预测精度都得到了显著提高，验证了SG滤波器能更好地保留时间序列特征并有效去除噪声。虽然ARIMA模型在单步预测上略优于SE-LSTM模型，但SE-LSTM在多步预测上优于ARIMA模型。观察到SE-LSTM在三个指标方面优于其同行。

DO数据集的比较结果：

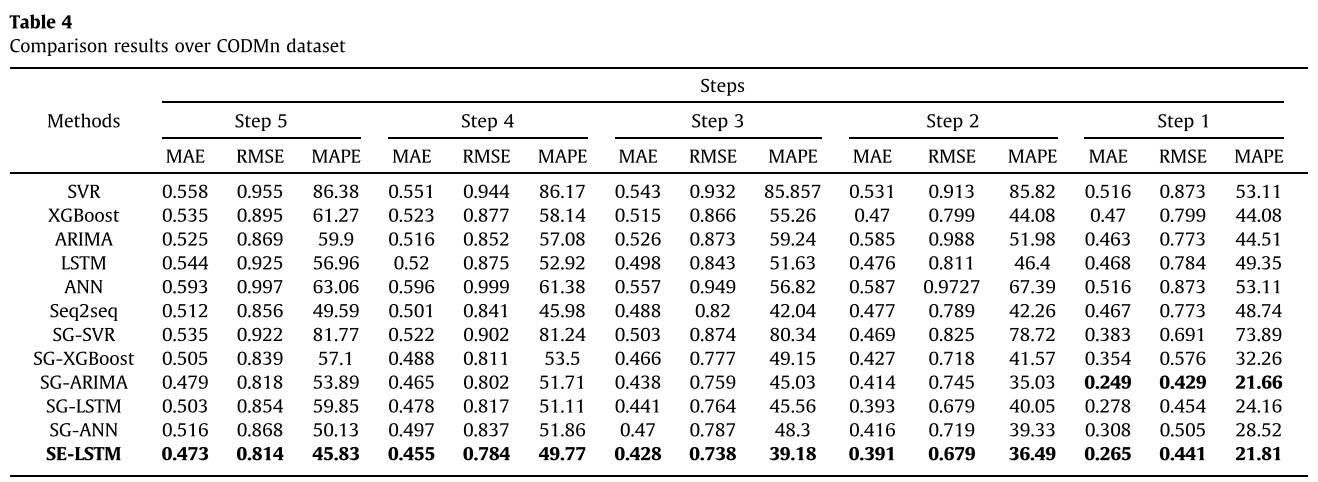
在CODMn数据集上的比较结果：

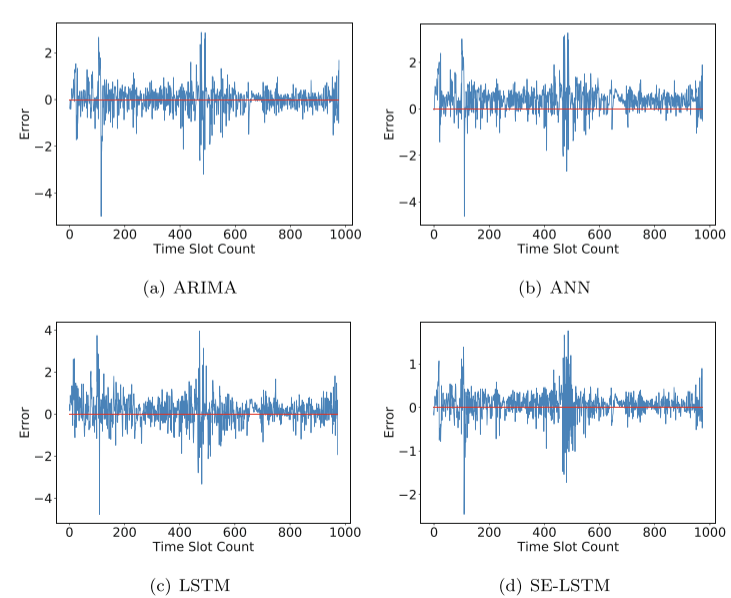
DO数据集上对比试验的图像：

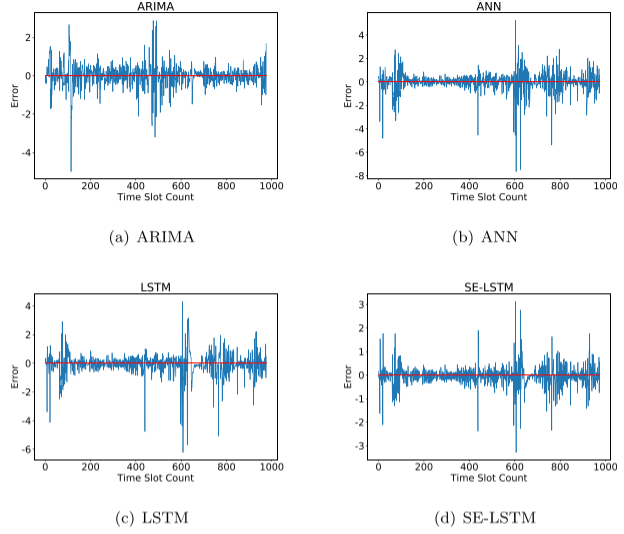
CODMn数据集上对比实验的图像

5. python环境下基于scipy实现SG滤波平滑

import matplotlib.pyplot as plt
import numpy as np
 
def SG01(data,window_size):
    # 前后各m个数据，共2m+1个数据，作为滑动窗口内滤波的值
    m = int((window_size - 1) / 2)  # (59-1)  /2 = 29
    # 计算 矩阵X 的值 ，就是将自变量x带进去的值算 0次方，1次方，2次方.....k-1次方,一共window_size行，k列
    # 大小为（2m+1,k）
    X_array = []
    for i in range(window_size):  #
        arr = []
        for j in range(3):
            X0 = np.power(-m + i, j)
            arr.append(X0)
        X_array.append(arr)
    X_array = np.mat(X_array)
    # B = X*（X.T*X）^-1*X.T
    B = X_array * (X_array.T * X_array).I * X_array.T
    data = np.insert(data, 0, [data[0] for i in range(m)])  # 首位插入m-1个data[0]
    data = np.append(data, [data[-1] for i in range(m)])  # 末尾插入m-1个data[-1]
    # 取B中的第m行 进行拟合  因为是对滑动窗口中的最中间那个值进行滤波，所以只要获取那个值对应的参数就行， 固定不变
    B_m = B[m]
    # 存储滤波值
    y_array = []
    # 对扩充的data 从第m个数据开始遍历一直到（data.shape[0] - m）  ：（第m个数据就是原始data的第1个，（data.shape[0] - m）为原始数据的最后一个
    for n in range(m, data.shape[0] - m):
        y_true = data[n - m: n + m + 1]  # 取出真实y值的前后各m个，一共2m+1个就是滑动窗口的大小
        y_filter = np.dot(B_m, y_true)  # 根据公式 y_filter = B * X 算的  X就是y_true
        y_array.append(float(y_filter))  # float(y_filter) 从矩阵转为数值型
    return y_array
 
if __name__ == '__main__':
    data = [0.3962, 0.4097, 0.2956, 0.4191, 0.3456, 0.3056, 0.6346, 0.7025, 0.6568, 0.4719, 0.5645, 0.6514, 0.5717,
            0.6072, 0.7076, 0.7062, 0.7086, 0.677, 0.8141, 0.7985, 0.7037, 0.7961, 0.6805, 0.5463, 0.2766]
    smoothed_data = SG01(data,5)
    smoothed_data = [round(i, 4) for i in smoothed_data]
    smoothed_data2 = SG01(data,11)
    smoothed_data2 = [round(i, 4) for i in smoothed_data2]
    print("data：", data)
    print("smoothed_data：", smoothed_data)
    print("smoothed_data2：", smoothed_data2)
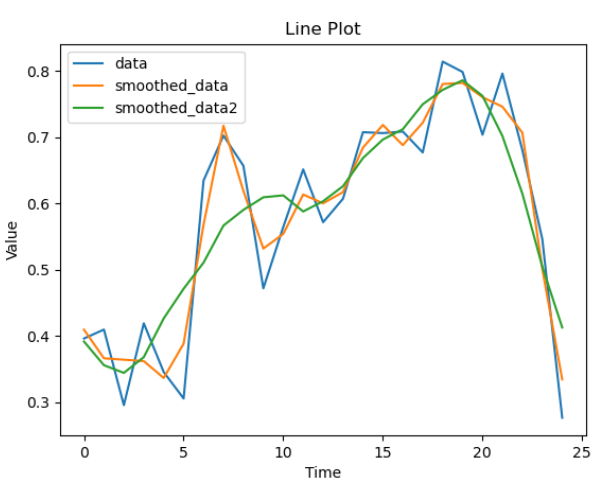
    plt.plot(data, label='data')
    plt.plot(smoothed_data, label='smoothed_data')
    plt.plot(smoothed_data2, label='smoothed_data2')
    plt.xlabel('Time')
    plt.ylabel('Value')
    plt.title('Line Plot')
    plt.legend()
    plt.show()

结论

该模型研究具有长短期记忆和 Savitzky-Golay 滤波器的编码器-解码器神经网络。由此产生的预测模型可以预测未来水质的时间序列。应用 Savitzky-Golay 滤波器来消除时间序列数据中的噪声。这项工作采用基于 LSTM 的编码器-解码器模型来捕获特征。最后，真实数据的实验结果证明，所提出的模型比几个基准模型提供了更准确的预测。

参考文献

[1] Jing Bi, Yongze Lin, Quanxi Dong, Haitao Yuan, MengChu Zhou “Large-scale water quality prediction with integrated deep neural network”, [J] https://doi.org/10.1016/j.ins.2021.04.057