A-1:树状数组
- 1.介绍
- Q1:树状数组解决什么问题?
- Q2:树状数组的使用
- 1.前置知识:lowbit(x)
- 2.单点修改
- 3.求[1,n]的和
- 4.区间查询
- 5.hh
- Q3:树状数组是否优化了
- Q4:上图上例子解释上面说的东西(Important)
- 2.习题练习
1.介绍
树状数组是一个比较难以理解的高级数据结构(至少我觉得很难😢)
由于难以理解,所以只好从以下几个方面去理解:
- 树状数组用于解决什么问题
- 如何去使用树状数组
- 树状数组是否优化了算法
- 用例子说明
新手不要去死钻“树状数组怎么被总结出来的?树状数组的发明过程”,如果有完美的回答感谢给个链接我去圆梦一下😢
!!对于这个学习,我的看法是先知道什么是树状数组,怎么写,然后根据数据和画图走几遍过程,然后做题。最后再去看数学推导(如果时间充裕的话)。
Q1:树状数组解决什么问题?
预告:数状数组解决”单点修改,区间查询(当然区间也可以是一个点)“问题
首先前缀和是大家都知道的基础算法。假设前缀和数组是
p
r
e
[
n
]
pre[n]
pre[n],原数组是
a
[
n
]
a[n]
a[n]
p
r
e
[
i
]
表示数组区间
[
0
,
i
]
之和
=
a
[
0
]
+
a
[
1
]
+
a
[
2
]
+
.
.
.
+
a
[
i
]
pre[i]表示数组区间[0,i]之和=a[0]+a[1]+a[2]+...+a[i]
pre[i]表示数组区间[0,i]之和=a[0]+a[1]+a[2]+...+a[i]
查询区间的时间复杂度是
O
(
1
)
O(1)
O(1),比如: 查询
[
i
,
j
]
[i,j]
[i,j]之和=
p
r
e
[
j
]
−
p
r
e
[
i
−
1
]
=
a
[
i
]
+
a
[
i
+
1
]
+
.
.
.
+
a
[
j
]
pre[j]-pre[i-1]=a[i]+a[i+1]+...+a[j]
pre[j]−pre[i−1]=a[i]+a[i+1]+...+a[j],很显然只需要一次操作即可。
重点来了!! 如果修改原数组的一个元素,假设
a
[
0
]
=
a
[
0
]
+
1
a[0]=a[0]+1
a[0]=a[0]+1,那么需要
p
r
e
[
0
]
+
1
pre[0]+1
pre[0]+1,
p
r
e
[
1
]
+
1
pre[1]+1
pre[1]+1…
p
r
e
[
n
]
+
1
pre[n]+1
pre[n]+1
总结发现,每次修改一个原数组元素,当前元素到数组末尾的所有元素的前缀和都需要改变,那么维护前缀和的时间复杂度是
O
(
n
)
O(n)
O(n),树状数组就是优化掉这个O(n)的大杀器!
总结一下:数状数组解决”单点修改,区间查询(当然区间也可以是一个点)“问题
Q2:树状数组的使用
😱😱😱😱😱
1.前置知识:lowbit(x)
l o w b i t ( x ) lowbit(x) lowbit(x),找x最低位的1及1右边(比1更低位)的所有数的总和,当然最低位1右边全是0
| x的十进制数 | x的二进制数 | lowbit(x)(换成十进制) |
|---|---|---|
| 10 | 1010 | 2 |
| 11 | 1011 | 1 |
| 12 | 1100 | 4 |
| 13 | 1101 | 1 |
| 14 | 1110 | 2 |
| 15 | 1111 | 1 |
| 16 | 0001 0000 | 16 |
现在应该是了解lowbit做一个什么事情,那么如何实现呢?
void lowbit(x)
{
return x&(-x);
}
对的,就是这么简单
对数取负表现为 ”除最高位,其余位取反,最低位加1”
来翻译一下: 令x=10
x=1010
-x=1110
x&(-x)=0010
Perfect😋。
2.单点修改
不同于前缀和数组,修改一个点,需要修改O(n)次前缀和区间,而树状数组只需要修改O(
log
2
n
\log_2 n
log2n)次
操作为
void add(int i, int y) //单点修改(同时可以初始化C数组)
{
for(;i<=n;i+=lowbit(i))
{
C[i]+=y;
}
}
3.求[1,n]的和
不同于前缀和O(1)次,查询前n个数的和需要O(
log
2
n
\log_2 n
log2n)次
操作为
int sum(int i) //前缀和,求[1,i]的和
{
int res=0;
for(;i>0;i-=lowbit(i))
res+=C[i];
return res;
}
4.区间查询
操作为
int Query(int i,int j) //查询[1,j]区间和
{
return sum(i)-sum(j-1);
}
5.hh
很显然,已经给出了单点修改,区间查询的操作,且时间复杂度实实在在更低更有效,比单纯使用前缀和好很多。那么有这些知识就可以去写题了。
Q3:树状数组是否优化了
和前缀和相比:
| 前缀和 | 树状数组 | |
|---|---|---|
| 区间查询 | O(1) | O( log 2 n \log_2 n log2n) |
| 单点修改 | O(n) | O( log 2 n \log_2 n log2n) |
当n非常大的时候
1
+
n
>
2
∗
(
log
2
n
)
1+n>2 *(\log_2 n)
1+n>2∗(log2n)
Q4:上图上例子解释上面说的东西(Important)
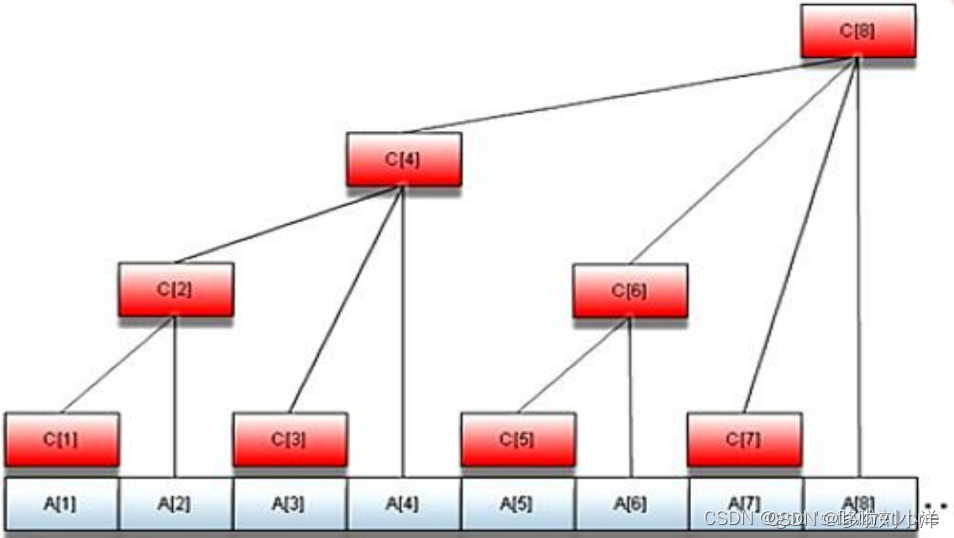
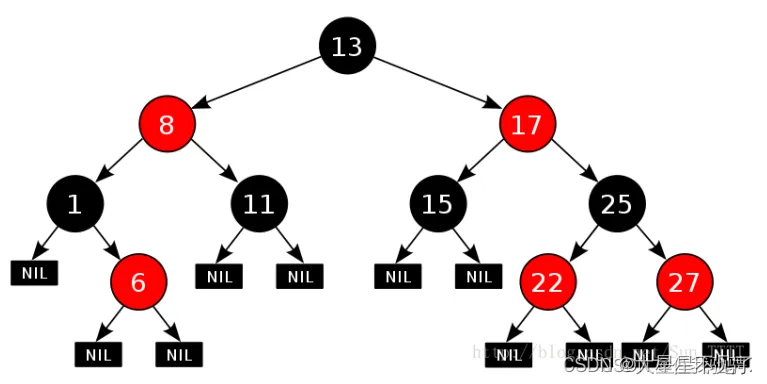
这个图是 借的,嗯,肯定是借的。
别被误导了!!,C数组不是前缀和,C[4]不是前4个数之和,这个数组单独看没有意义,只有和函数配合使用才有意义!!
现在先抛出问题:需要对数组进行单点修改,区间查询。
现在有数组
A
[
1
]
.
.
.
A
[
8
]
=
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
A[1]... A[8]={1,2,3,4,5,6,7,8}
A[1]...A[8]=1,2,3,4,5,6,7,8
先初始化树状数组C,这个数组单独不代表什么,要和其它操作一起才有意义
void add(int i, int y) //单点修改(同时可以初始化C数组)
{
for(;i<=n;i+=lowbit(i))
{
C[i]+=y;
}
}
| C[i]+=y | i+=lowbit(i),C[i]+=y | i+=lowbit(i) ,C[i]+=y | i+=lowbit(i),C[i]+=y |
|---|---|---|---|
| C[1]+=1 | C[2]+=1 | C[4]+=1 | C[8]+=1 |
| C[2]+=2 | C[4]+=2 | C[8]+=2 | |
| C[3]+=3 | C[4]+=3 | C[8]+=3 | |
| C[4]+=4 | C[8]+=4 | ||
| C[5]+=5 | C[6]+=5 | C[8]+=5 | |
| C[6]+=6 | C[8]+=6 | ||
| C[7]+=7 | C[8]+=7 | ||
| C[8]+=8 |
| i | C[i] |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 3 |
| 4 | 10 |
| 5 | 5 |
| 6 | 11 |
| 7 | 7 |
| 8 | 36 |
这就是初始化树状数组,那么先来看查询。
查询 (对照上面的表看,自己琢磨一下)
int sum(int i) //前缀和,求[1,i]的和
{
int res=0;
for(;i>0;i-=lowbit(i))
res+=C[i];
return res;
}
| i | sum(i) |
|---|---|
| 1 | res=C[1]=1 |
| 2 | res=C[2]=3 |
| 3 | res=C[3]+C[2]=6 |
| 7 | res=C[7]+C[6]+C[4]=28 |
| 8 | res=C[8]=36 |
2.习题练习
给个链接,兄弟们去刷吧😋
洛谷树状数组题集
Leetcode树状数组题集
洛谷的先做题集里面的模板题
稍后把我的题解搬几个过来。