目录
一、插入排序
1、直接插入排序
2、希尔排序(缩小增量排序)
二、选择排序
3、直接选择排序
4、堆排序
三、交换排序
5、冒泡排序
6、快速排序
四、归并排序
7、归并排序
五、总结
一、插入排序
1、直接插入排序
思路:
i 用来遍历数组,拿到一个就放进 tmp,
j 从 i 的前一个开始,每次都和 tmp里的值进行比较,若比tmp的值大,j 的值给到 j+1,j--
直到 j 的值比tmp小,或者 j 减到 <0,循环结束,tmp 的值给到 j+1
- 时间复杂度:最坏情况下,逆序,O(n^2);最好情况下,有序,O(n)
- 空间复杂度:O(1)
- 稳定性:稳定
- 特点:当数据量不多,且基本上趋于有序时,使用直接插入排序很快,趋于O(n)
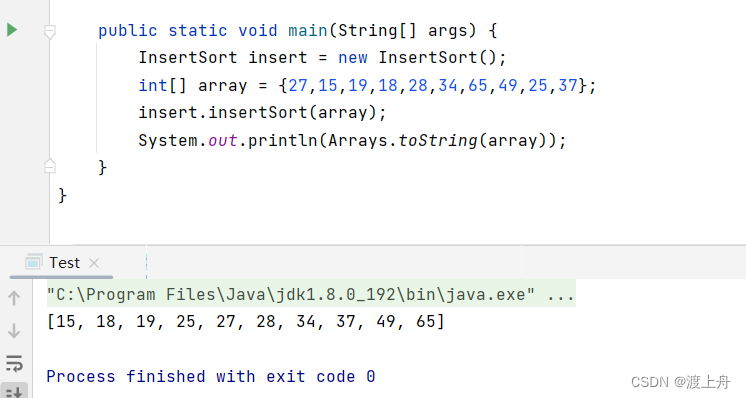
public class InsertSort {
public void insertSort(int[] array){
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0; j--) {
if(array[j] > tmp){
array[j+1] = array[j];
}else{
break;
}
}
array[j+1] = tmp;
}
}
} 
2、希尔排序(缩小增量排序)
- 时间复杂度:O(n^1.3)
- 空间复杂度:O(1)
- 稳定性:不稳定
- 特点:是对直接插入排序的优化,在最后进行直接插入排序之前,增加了预排序。
/*
希尔排序(缩小增量排序):gap每次除2
*/
public class ShellSort {
public void shellSort(int[] array){
int gap = array.length;
while(gap > 1){
gap /= 2;
shell(array,gap);
}
}
public void shell(int[] array,int gap){
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if(array[j] > tmp){
array[j+gap] = array[j];
}else{
break;
}
}
array[j+gap] = tmp;
}
}
}
二、选择排序
3、直接选择排序
思路:(走一遍,找到一个最小值)
i 用来遍历数组,拿到一个下标就放进 mIndex
j 从 i 的后一个开始,遍历数组,遇到比 mIndex里的值 小的就更新 mIndex
这一轮遍历完,mIndex里存的就是最小值的下标,把 i 和 mIndex 下标的元素 交换,i++
优化后的思路:(用left 和 right 来遍历数组,走一遍能找到一个最小值和一个最大值)
left 和 right 分别指向 数组的左右两边,minIndex 和 maxIndex 的初始值是 left
j 从 left 的后一个开始遍历,遍历数组 [left+1,right],遇到比 minIndex里的值 小的就更新 minIndex,遇到比 maxIndex里的值 大的就更新 maxIndex
这一轮遍历完,minIndex里存的就是最小值的下标,maxIndex里存的就是最大值的下标,然后把 left 和 minIndex 下标的元素交换,把 right 和 maxIndex 下标的元素交换,left++,right--,但如果 maxIndex 刚好是left,那么最大值就会被换到 minIndex 下标的位置,就得先更新一下 maxIndex,让 maxIndex = minIndex
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
public class SelectSort {
public void selectSort(int[] array){
for (int i = 0; i < array.length; i++) {
int mIndex = i;
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[mIndex]){
mIndex = j;
}
}
//走到这,mIndex里存的是[i,array.length)中最小值的下标
int tmp = array[i];
array[i] = array[mIndex];
array[mIndex] = tmp;
}
}
}优化后:
public void select(int[] array){
int left = 0;
int right = array.length-1;
while(left < right){
int minIndex = left;
int maxIndex = left;
for (int j = left+1; j <= right; j++) {
if(array[j] < array[minIndex]){
minIndex = j;
}
if(array[j] > array[maxIndex]){
maxIndex = j;
}
}
//走到这,minIndex存的是最小值的下标,maxIndex存的是最大值的下标
swap(array, left, minIndex);
//如果最大值的下标是left
if(maxIndex == left){
maxIndex = minIndex;
}
swap(array, right, maxIndex);
left++;
right--;
}
}
public void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}4、堆排序
- 时间复杂度:O(n*log n)
- 空间复杂度:O(1)
- 稳定性:不稳定
- 堆排的时间复杂度:建大根堆的时间复杂度+排序的时间复杂度,建大根堆的时间复杂度:O(n),排序的时间复杂度:O(n*log n) —— 每次shiftDown 0的时间复杂度是 log n,要 n-1 次,所以堆排的时间复杂度:O(n)+O(n*log n) ≈ O(n*log n)
public class HeapSort {
public void heapSort(int[] array){
//首先,建一个大根堆
createBigHeap(array);
//然后排序
int end = array.length-1;
while(end > 0){
swap(array,0,end);
shiftDown(array,0,end);
end--;
}
}
public void createBigHeap(int[] array){
for (int parent = (array.length-1-1)/2; parent >= 0; parent--) {
//每个子树都需要向下调整成大根堆
shiftDown(array,parent,array.length);
}
}
public void shiftDown(int[] array,int parent,int end){
int child = 2*parent+1;
while(child < end){
if(child+1 < end && array[child] < array[child+1]){
child++;
}
if(array[child] > array[parent]){
swap(array,child,parent);
parent = child;
child = 2*parent+1;
}else{
break;
}
}
}
public void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}
三、交换排序
5、冒泡排序
思路:
相邻的两个元素进行比较,i 是趟数,j 是每一趟要比较的次数,每一趟都会把一个最大值放到后面。
- 时间复杂度:(不考虑优化)O(n^2),如果考虑优化的话,最好情况下可以达到O(n)
- 空间复杂度:O(1)
- 稳定性: 稳定
public class BubbleSort {
public void bubbleSort(int[] array){
//趟数
for (int i = 0; i < array.length-1; i++) {
boolean flag = true;
//1趟
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]){
swap(array,j,j+1);
flag = false;
}
}
//如果flag还是true,说明这一趟中没有进入过if语句进行交换,说明是元素是有序的
if(flag){
break;
}
}
}
public void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}6、快速排序
- 时间复杂度:O(n*logn)
- 空间复杂度:O(logn)
- 稳定性:不稳定
- 时间复杂度:每层遍历的都是n,要遍历树的高度层,树的高度是logn,所以时间复杂度是nlogn;空间复杂度:需要额外开辟的空间就是存pivot这个基准需要的空间,由于当左边递归完去递归右边时,左边给基准开辟的空间就会被回收,所以需要额外给pivot开辟的空间就是树的高度,所以空间复杂度是logn
- 上述快排的时间复杂度和空间复杂度不是最坏的,当数据是顺序或逆序时,二叉树只有左树或只有右树,达到最坏,此时时间复杂度是O(n^2),空间复杂度是O(n)
但我们可以优化代码,不让它出现只有左树或只有右树的情况。
1、优化方法一:(解决划分不均匀的问题)
定义一个mid = (start+end)/2
在找基准之前,判断 start,end,mid,三个下标对应的值,谁是中间的那个,返回下标。
然后,与start下标进行交换。尽量解决划分不均匀的问题
2、优化方法二:(减少后几层的递归,解决效率问题)
递归到小的子区间时,可以考虑使用插入排序。
我们发现,后几层占了整棵树的大部分结点,递归的次数最多发生在后面。所以,我们可以减少后几层的递归来解决效率问题。递归区间很小的时候,我们就不递归了,使用直接插入排序。(这时数据页越来越有序了,使用直接插入排序的时间复杂度趋近O(n),是很快的)
(1)Hoare 法:
找基准:
把left的下标记录下来为i,并把left下标对应的值放进tmp,
从右边找到一个比tmp小的,从左边找到一个比tmp大的,然后交换。这个过程是个循环,循环的条件是 left < right,一旦left和right相等了,就会出循环,此时left和right下标就是基准,交换i和基准对应的值。到这里,基准的左边都是比它小的(或等于它的),基准的右边都是比它大的(或等于它的)
public class QuickSort {
public void quick(int[] array,int start,int end){
if(start >= end){
return;
}
// end-start+1 是 [start,end]这个区间元素的个数
if(end-start+1 <= 15){
//对 start 和 end 区间范围内使用插入排序
insertSort(array,start,end);
return;
}
//找三个值中中间值的下标
int mid = findMidOfIndex(array,start,end);
swap(array,mid,start);
//找基准
int pivot = partition(array,start,end);
//pivot 就是基准,然后分而治之
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
public void quickSort(int[] array){
quick(array,0,array.length-1);
}
public void insertSort(int[] array,int start,int end){
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= start; j--) {
if(array[j] > tmp){
array[j+1] = array[j];
}else{
break;
}
}
array[j+1] = tmp;
}
}
private int findMidOfIndex(int[] array, int start, int end) {
int mid = (start+end)/2;
if(array[start] < array[end]){
if(array[mid] < array[start]){
return start;
}else if(array[mid] > array[end]){
return end;
}else{
return mid;
}
}else{
if(array[mid] > array[start]){
return start;
}else if(array[mid] < array[end]){
return end;
}else{
return mid;
}
}
}
public int partition(int[] array,int left,int right){
//把left下标记录下来,并把值放进tmp,后面都和tmp进行比较
int i = left;
int tmp = array[left];
// left < right 不能是 <= ,当 left == right 时,说明这一趟走完了,基准的下标找到了
while(left < right){
/*
* 要先从右边找到一个比tmp小的,再从左边找到一个比tmp大的,不能反过来
* 因为如果反过来了,就可能会出现我从左边找到了一个比tmp大的后,开始从右边找比tmp小的,
* 但是还没有找到left和right就相等了。此时,left和right下标对应的值就是比tmp大的值
* 出循环后, swap(array,i,left) 就会将大的值换到基准前面去。所以不能反过来。
* 按照先从右边找一个比tmp小的的方式,我们会先找到一个比tmp小的,即使还没找到比tmp大的就相遇了,
* left和right下标对应的值也是比tmp小的值,交换后会将小的值放到前面。
* 所以,一定要先从右边找比tmp小的值!!!
*/
//从右面找到一个比tmp小的
while(left < right && array[right] >= tmp){
right--;
}
//从左面找到一个比tmp大的
while(left < right && array[left] <= tmp){
left++;
}
//从到这,left下标里存的是比tmp大的值,right下标里存的是比tmp小的值
swap(array,left,right);
}
swap(array,i,left);
return left;
}
public void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}
(2)挖坑法: (做题优先使用挖坑法)
找基准:
把left下标对应的值放进tmp,
从右边找到一个比tmp小的(下标是right),放进left下标的坑;再从左边找到一个比tmp大的(下标是left),放进right下标的坑。这个过程是个循环,循环的条件是 left<right,直到left和right相等,退出循环,此时left和right就是基准。将tmp放进基准的这个坑里。到这里,基准的左边都是比它小的(或等于它的),基准的右边都是比它大的(或等于它的)
public class QuickSort2 {
public void quickSort(int[] array){
quick(array,0,array.length-1);
}
private void quick(int[] array, int start, int end) {
//先找基准,然后找基准左边的基准,然后找基准右边的基准
if(start >= end){
return;
}
// end-start+1 是 [start,end]这个区间元素的个数
if(end-start+1 <= 15){
//对 start 和 end 区间范围内使用插入排序
insertSort(array,start,end);
return;
}
//找三个值中中间值的下标
int mid = findMidOfIndex(array,start,end);
swap(array,mid,start);
//找基准
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
public void insertSort(int[] array,int start,int end){
for (int i = start+1; i <= end; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= start; j--) {
if(array[j] > tmp){
array[j+1] = array[j];
}else{
break;
}
}
array[j+1] = tmp;
}
}
private int findMidOfIndex(int[] array, int start, int end) {
int mid = (start+end)/2;
if(array[start] < array[end]){
if(array[mid] < array[start]){
return start;
}else if(array[mid] > array[end]){
return end;
}else{
return mid;
}
}else{
if(array[mid] > array[start]){
return start;
}else if(array[mid] < array[end]){
return end;
}else{
return mid;
}
}
}
private int partition(int[] array, int left, int right) {
int tmp = array[left];
while(left < right){
while(left < right && array[right] >= tmp){
right--;
}
array[left] = array[right];
while(left < right && array[left] <= tmp){
left++;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
private void swap(int[] array, int x, int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}
四、归并排序
7、归并排序
思路:
先分解,再合并
分解到一个一个的元素(递),然后合并(归)
主要逻辑就是,将两个有序的数组合并成一个有序的数组。
- 时间复杂度:O(n*logn)
- 空间复杂度:O(n)
- 稳定性:稳定
public class MergeSort {
public void mergeSort(int[] array){
int start = 0;
int end = array.length-1;
int mid = (start+end)/2;
mergeSortChild(array,start,mid,end);
}
public void mergeSortChild(int[] array,int start,int mid,int end){
if(start == end){
return;
}
int s1 = 0;
int e1 = mid;
int s2 = mid+1;
int e2 = end;
//分解:分解到start==end,即只有一个元素
mergeSortChild(array,s1,(s1+e1)/2,e1);
mergeSortChild(array,s2,(s2+e2)/2,e2);
//合并
merge(array,s1,e1,s2,e2);
}
//把两个有序数组合成一个有序的数组
public void merge(int[] array,int s1,int e1,int s2,int e2){
int s = s1;
int[] tmpArr = new int[e2-s1+1];
int k = 0;
while(s1<=e1 && s2<=e2){
if(array[s1] < array[s2]){
tmpArr[k++] = array[s1++];
}else{
tmpArr[k++] = array[s2++];
}
}
while(s1 <= e1){
tmpArr[k++] = array[s1++];
}
while(s2 <= e2){
tmpArr[k++] = array[s2++];
}
for (int i = 0; i < k; i++) {
array[s+i] = tmpArr[i];
}
}
}
五、总结
| 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 |
| 直接插入排序 | O(n^2) 最好情况下:O(n) | O(1) | 稳定 |
| 希尔排序 | O(n^1.3) | O(1) | 不稳定 |
| 直接选择排序 | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n*logn) | O(1) | 不稳定 |
| 冒泡排序 | O(n^2) 最好情况下:O(n) | O(1) | 稳定 |
| 快速排序 | O(n*logn) 最坏情况下:O(n^2) | O(logn) 最坏情况下:O(n) | 不稳定 |
| 归并排序 | O(n*logn) | O(n) | 稳定 |