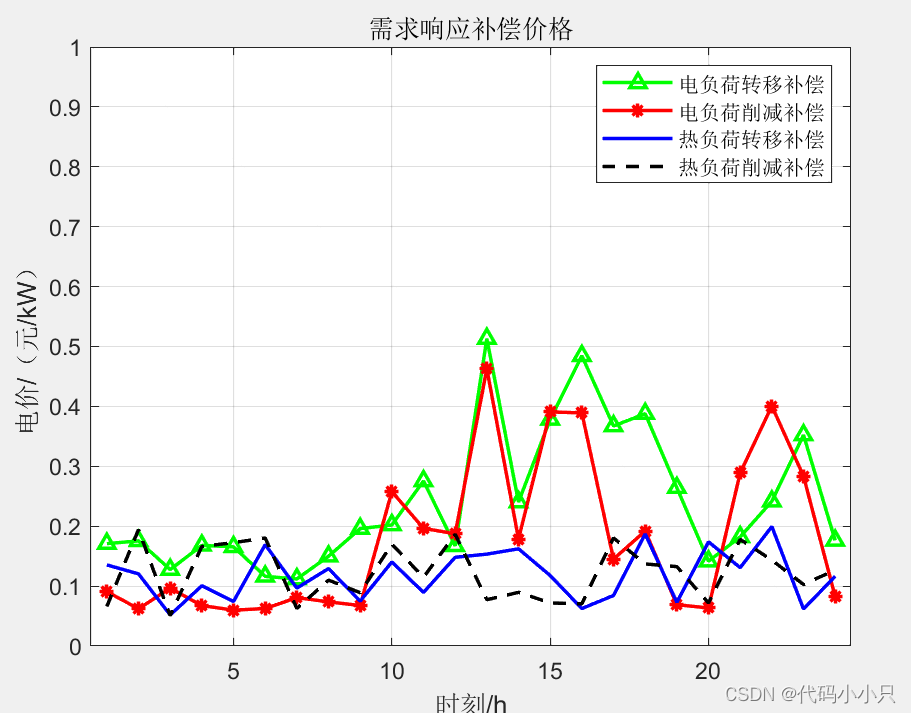
随着能源市场由传统的垂直一体式结构向交互竞争型 结构转变,社区综合能源系统的分布式特征愈发明显,传统 的集中优化方法难以揭示多主体间的交互行为。该文提出一 种基于主从博弈的社区综合能源系统分布式协同优化运行 策略,将综合能源销售商作为领导者,新能源冷热电联供运 营商和负荷聚合商作为跟随者,求解各方在追求目标最优时 的交互策略。首先,介绍社区综合能源系统的交易模式及数 学模型,并将其嵌入到主从博弈框架下,建立一主多从的分 布式协同优化模型。其次,证明 Stackelberg 均衡的唯一性, 并通过遗传算法和二次规划相结合的算法求解。最后,通过 算例验证所提方法的有效性,供能侧的收益和用能侧的消费 者剩余同时得到提升。
部分代码:
clc
clear;
Max_Dt=20;%最大迭代次数300
D=144;%搜索空间维数(未知数个数) (1-24为售电价格,25-48为售热价格,49-96电需求响应价格,96-144为热需求响应价格)
N=10;%粒子个数600
w_max=0.9;
w_min=0.4;
v_max=0.2;
s=1;
%%%%%粒子初始化%%%%%
x=zeros(N,D);
for i=1:N
for j=1:9
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.03;
end
for j=10:12
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.45;
end
for j=13:16
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.85;
end
for j=17:20
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.45;
end
for j=21:22
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.85;
end
for j=23:24
v(i,j)=0.0;
x(i,j)=0.35+rand()*0.45;
end
for j=25:48
v(i,j)=0.0;
x(i,j)=0.2+rand()*0.3;
end
for j=1+48:9+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.1;
end
for j=10+48:12+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.3;
end
for j=13+48:16+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.55;
end
for j=17+48:20+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.3;
end
for j=21+48:22+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.55;
end
for j=23+48:24+48
v(i,j)=0.0;
x(i,j)=0.1+rand()*0.3;
end
for j=1+72:9+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.05;
end
for j=10+72:12+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.25;
end
for j=13+72:16+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.45;
end
for j=17+72:20+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.25;
end
for j=21+72:22+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.45;
end
for j=23+72:24+72
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.25;
end
for j=97:144
v(i,j)=0.0;
x(i,j)=0.05+rand()*0.15;
end
end