一、顺序栈
顺序栈的存储方式如下:
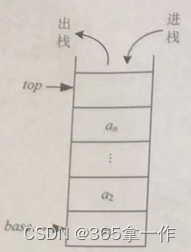
从图中可以看出,顺序栈需要两个指针,base指向栈底,top指向栈顶。
typedef struct SqStack {
ElemType *base; //栈底指针
ElemType *top; //栈顶指针
}SqStack;说明:
ElemType是元素类型,需要什么类型就写什么类型。
typedef将结构体等价于类型名Sqstack。
栈定义好了之后,还要先定义一个最大的分配空间,这和数组一样,需要预先分配空间,因此可以采用宏定义:
#define Maxsize 100; //预先分配空间,这个数值根据实际需要预估确定
上面的结构体定义采用了动态分配的形式,也可以采用静态分配的形式,使用一个长数组存储数据元素,一个整型下标记录栈顶元素的位置。静态分配的顺序栈结构定义如下:
typedef struct SqStack {
ElemType data[Maxsize]; //定长数组
int top; //栈顶下标
}SqStack;注意:栈只能在一端操作,后进先出,是人为规定的,也就是说不允许在中间查找,取值,插入,删除等操作。顺序栈本身是顺序存储的,有人就想:我偏要从中间取一个元素,这也是可以的,但这样做,这就不是栈了。
1、顺序栈的初始化
初始化一个空栈,动态分配Maxsize大小的空间,用S.top和S.base指向该空间的基地址。
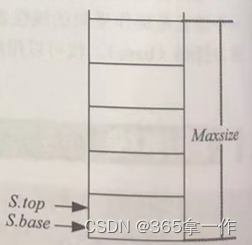
代码实现:
bool InitStack(SqStack &S) //构造一个空栈S
{
S.base=new int[Maxsize];//为顺序栈分配一个最大容量为Maxsize的空间
if(!S.base) //空间分配失败
return false;
S.top=S.base; //top初始为base,空栈
return true;
}2、入栈
入栈前要判断是否栈满,如果栈已满,则入栈失败;否则将元素放入栈顶,栈顶指针向上移动一个位置(top++)。
图解:

输入1,入栈(左图)
接着输入2,入栈(右图)
代码实现:
bool Push(SqStack &S,int e) // 插入元素e为新的栈顶元素
{
if(S.top-S.base==Maxsize) //栈满
return false;
*(S.top++)=e; //元素e压入栈顶,然后栈顶指针加1,等价于*S.top=e; S.top++;
return true;
}3、出栈
出栈前要先判断是否为空栈,如果栈是空的,则出栈失败;否则将栈顶元素暂存给一个变量,栈顶指针向下移动一个位置(top--)。

完美图解:
栈顶元素所在的位置是S.top-1,因此把该元素取出来,暂存在变量e中,然后S.top指针向下移动一个位置。因此可以先移动一个位置,即--S.top,然后再取出元素。
例:栈顶元素4出栈前后的状态
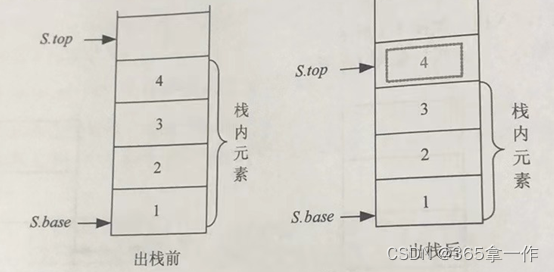
注意:因为顺序栈删除一个元素时,并没有销毁该空间,所以4其实还在那个位置,只不过下一次再有元素进栈时,就把他覆盖了。相当于该元素已出栈,因为栈的内容时S.base到S.top-1。
代码实现:
bool Pop(SqStack &S,int &e) //删除S的栈顶元素,暂存在变量e中
{
if(S.base==S.top) //栈空
return false;
e=*(--S.top); //栈顶指针减1,将栈顶元素赋给e
return true;
}4、取栈顶元素
取栈顶元素和出栈不同。取栈顶元素只是把栈顶元素复制一份,栈顶指针未移动,栈内元素个数未变。而出栈时栈顶指针向下移动一个位置,栈内不在包含这个元素。
完美图解:

取栈顶元素*(S.top-1)即元素4,取值后S.top指针没有改变,栈内元素的个数也没有改变。
代码实现:
int GetTop(SqStack S) //返回S的栈顶元素,栈顶指针不变
{
if(S.top!=S.base) //栈非空
return *(S.top-1); //返回栈顶元素的值,栈顶指针不变
else
return -1;
}二、链栈
栈可以顺序存储,也可以用链式存储。
顺序栈是分配一段连续的空间,需要两个指针:base指向栈底,top指向栈顶,而链栈每个节点的地址都不连续,只需要一个栈顶指针即可。

链栈的每个节点都包含两个域:数据域和指针域。可以把链栈看作一个不带头结点的单链表,但只能在头部进行插入、删除、取值等操作,不可以在中间和尾部操作。
链栈的结构体定义如下:
typedef struct Snode{
ElemType data; //数据域
struct Snode *next; //指针域,指向下一个节点的指针
}Snode,*LinkStack;链栈的节点定义和单链表一样,只不过它只能在栈顶那一端操作而已。
1、链栈的初始化
初始化一个空的链栈是不需要头结点的,因此只需要让栈顶指针为空即可。
代码实现:
typedef struct Snode{
ElemType data; //数据域
struct Snode *next; //指针域,指向下一个节点的指针
}Snode,*LinkStack;2.入栈
入栈是将新元素节点压入栈顶。因为链栈中第一个节点为栈顶,因此将新元素节点插入到第一个节点的前面,然后修改栈顶指针指向新结点即可。有点像堆柴,将新的节点堆在栈顶之上,新的节点成为新的栈顶。
完美图解:
(1)生成新结点。入栈前要创建一个新结点,将元素e存入该结点的数据域。
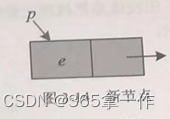
代码实现:
p=new Snode; //生成新结点,用p指针指向该结点
p->data=e; //将e放在新结点数据域(2)将新元素节点插入到第一个节点的前面,然后修改栈顶指针指向新结点。

赋值解释:
- p->next=S; //将新结点的指针域指向S,即将S的地址赋值给新结点的指针域。
- S=p; //修改栈顶指针为p
整体代码实现:
bool Push(LinkStack &S,int e) //在栈顶插入元素e
{
LinkStack p;
p=new Snode; //生成新结点
p->data=e; //将e放在新结点数据域
p->next=S; //将新结点的指针域指向S,即将S的地址赋值给新结点的指针域
S=p; //修改栈顶指针为p
return true;
}3.出栈
出栈就是把栈顶元素删除,绕过指针指向下一个节点,然后释放该结点空间。
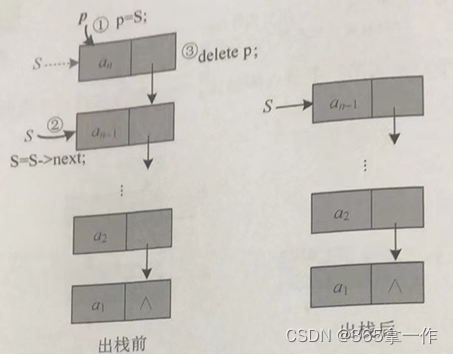
赋值解释:
- p=S; //用p保存栈顶元素地址,以备释放
- S=S->next; //修改栈顶指针,指向下一个结点
- delete p; //释放原栈顶元素的空间
代码实现:
bool Pop(LinkStack &S,int &e) //删除S的栈顶元素,用e保存其值
{
LinkStack p;
if(S==NULL) //栈空
return false;
e=S->data; //将栈顶元素赋给e
p=S; //用p保存栈顶元素地址,以备释放
S=S->next; //修改栈顶指针,指向下一个结点
delete p; //释放原栈顶元素的空间
return true;
}4.取栈顶元素
取栈顶元素和出栈不同,取栈顶元素只是把栈顶元素赋值一份,栈顶指针并没有改变。而出栈是指删除栈顶元素,栈顶指针指向了下一个元素。
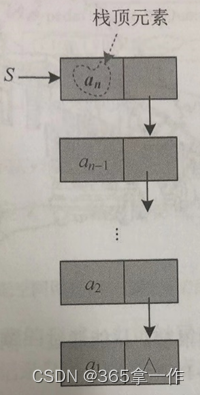
代码实现:
int GetTop(LinkStack S) //返回S的栈顶元素,不修改栈顶指针
{
if(S!=NULL) //栈非空
return S->data; //返回栈顶元素的值,栈顶指针不变
else
return -1;
}顺序栈和链栈的所以基本操作都只需要常数事件,所以在事件效率上难分伯仲。在空间效率方面,顺序栈需要预先分配固定长度的空间,有可能造成空间浪费或溢出;链栈每次只分配一个节点,除非没有内存,否则不会出现溢出,但是每个节点需要一个指针域,结构性开销增加。因此,如果元素个数变化较大,可以采用栈链;反之,可以采用顺序栈。在实际中,顺序栈比链栈应用更广泛。
配套完整代码(顺序栈):
#include<iostream>
using namespace std;
#define Maxsize 100 //预先分配空间,这个数值根据实际需要预估确定;
typedef struct SqStack {
int *base; //栈底指针
int *top; //栈顶指针
}SqStack;
bool InitStack(SqStack &S) //构造一个空栈S
{
S.base=new int[Maxsize];//为顺序栈分配一个最大容量为Maxsize的空间
if(!S.base) //空间分配失败
return false;
S.top=S.base; //top初始为base,空栈
return true;
}
bool Push(SqStack &S,int e) // 插入元素e为新的栈顶元素
{
if(S.top-S.base==Maxsize) //栈满
return false;
*(S.top++)=e; //元素e压入栈顶,然后栈顶指针加1,等价于*S.top=e; S.top++;
return true;
}
bool Pop(SqStack &S,int &e) //删除S的栈顶元素,暂存在变量e中
{
if(S.base==S.top) //栈空
return false;
e=*(--S.top); //栈顶指针减1,将栈顶元素赋给e
return true;
}
int GetTop(SqStack S) //返回S的栈顶元素,栈顶指针不变
{
if(S.top!=S.base) //栈非空
return *(S.top-1); //返回栈顶元素的值,栈顶指针不变
else
return -1;
}
int main()
{
int n,x;
SqStack S;
InitStack(S);//初始化一个顺序栈S
cout<<"请输入元素个数n:"<<endl;
cin>>n;
cout<<"请依次输入n个元素,依次入栈:"<<endl;
while(n--)
{
cin>>x; //输入元素
Push(S,x);
}
cout<<"元素依次出栈:"<<endl;
while(S.top!=S.base)//如果栈不空,则依次出栈
{
cout<<GetTop(S)<<"\t";//输出栈顶元素
Pop(S,x); //栈顶元素出栈
}
return 0;
}配套完整源代码(链栈):
#include<iostream>
using namespace std;
typedef struct Snode{
int data; //数据域
struct Snode *next; //指针域
}Snode,*LinkStack;
bool InitStack(LinkStack &S)//构造一个空栈S
{
S=NULL;
return true;
}
bool Push(LinkStack &S,int e) //在栈顶插入元素e
{
LinkStack p;
p=new Snode; //生成新结点
p->data=e; //将e放在新结点数据域
p->next=S; //将新结点的指针域指向S,即将S的地址赋值给新结点的指针域
S=p; //修改栈顶指针为p
return true;
}
bool Pop(LinkStack &S,int &e) //删除S的栈顶元素,用e保存其值
{
LinkStack p;
if(S==NULL) //栈空
return false;
e=S->data; //将栈顶元素赋给e
p=S; //用p保存栈顶元素地址,以备释放
S=S->next; //修改栈顶指针,指向下一个结点
delete p; //释放原栈顶元素的空间
return true;
}
int GetTop(LinkStack S) //返回S的栈顶元素,不修改栈顶指针
{
if(S!=NULL) //栈非空
return S->data; //返回栈顶元素的值,栈顶指针不变
else
return -1;
}
int main()
{
int n,x;
LinkStack S;
InitStack(S);//初始化一个顺序栈S
cout<<"请输入元素个数n:"<<endl;
cin>>n;
cout<<"请依次输入n个元素,依次入栈:"<<endl;
while(n--)
{
cin>>x; //输入元素
Push(S,x);
}
cout<<"元素依次出栈:"<<endl;
while(S!=NULL)//如果栈不空,则依次出栈
{
cout<<GetTop(S)<<"\t";//输出栈顶元素
Pop(S,x); //栈顶元素出栈
}
return 0;
}