目录
正文
1 曲线方程
2 点的运算
3 求解过程
4 补充:有限域
⚠️ 知乎:【密码专栏】动手计算双线性对(中) - 知乎
⚠️ 写在前面:本文属搬运博客,自己留着学习。注意,这篇博客与前三篇博客来源于不同网站,因此没有逻辑联系。在本文中,你将看到一个椭圆曲线的循环群是如何诞生的。
正文
上一篇分享了 “模运算” 相关的知识,并且计算了一些有限域的例子,这一篇我们讨论在通用零知识证明中经常提到的椭圆曲线和双线性配对。
很遗憾,尚未找到所谓的 “上一篇” 文章。此外,这篇文章也没有讲双线性对。
椭圆曲线作为双线性对的基础和前置知识,我们首先介绍一下其在实数域上的表现形式,然后通过计算的方法列出 “F_{101}” 上的全部元素的列表。
有限域一般用 “F_P” 来表示,其大小是大素数 P 。在这个有限域中,包含了 P 个元素,包括数字 0 到 P-1 。这里的 “F_{101}”(Latex 写法)表示素数为 101 的有限域。
1 曲线方程
椭圆曲线的一般形式的方程其实比较复杂,称为 Weierstrass 方程,形如下面的形式:
区块链中的椭圆曲线用的不是一般形式,而是后文提到的简化形式。
我们先将 a, b, c, d, e 随意的取值为 1, 2, 3, 4, 5,并通过画图来查看曲线在直角坐标系上的表现形式。根据二次方程求根公式(假设求根公式可用),我们将其变换为 x 关于 y 的函数:
二次方程求根公式就是我们在初中会学习的那个求根公式。
根据方程作图如下:
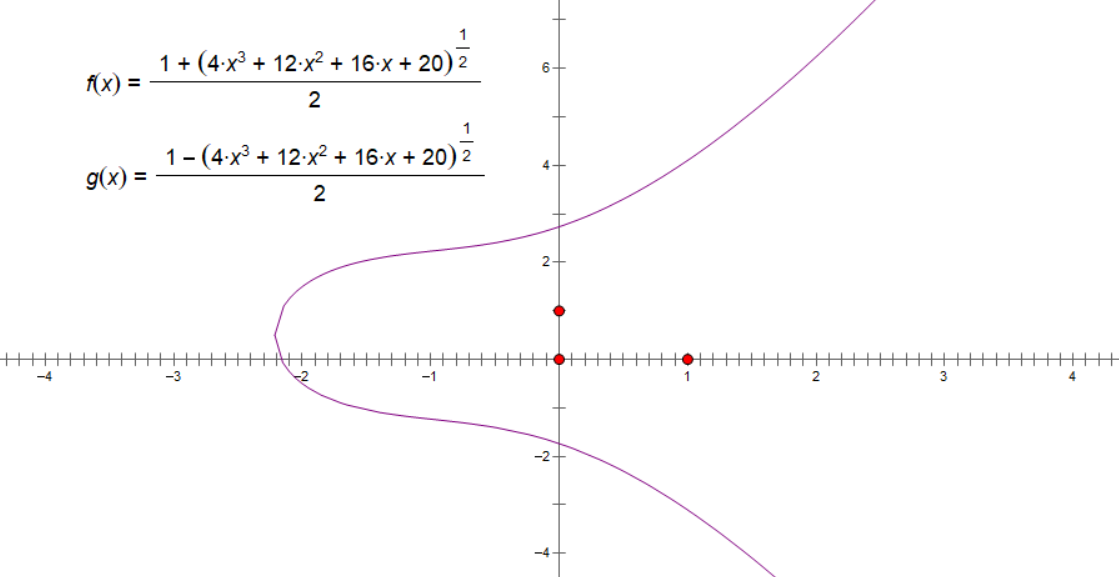
用几何画板画的图。
根据上面的方程和作图过程了解到,曲线由上下两个半支组成,关于 y=0.5 对称。
求解 f(x) = g(x) 时的 (x, y) 就能得到 y=0.5,可惜我已经不是高中生。
对称的总是美的,但是这个曲线却有一点瑕疵,它的对称轴并不是 x 轴而是 y=0.5。考虑到 Weierstrass 太过复杂,人们更经常使用的是在 Weierstrass 方程的基础上进行一些坐标变换(平移和缩放)和参数化简后的形式。该形式关于 x 轴对称:
当取 a=0,b=3 时,画出曲线如下图,容易验证 (1, 2) 是曲线上一点,对称的 (1, -2) 也是。
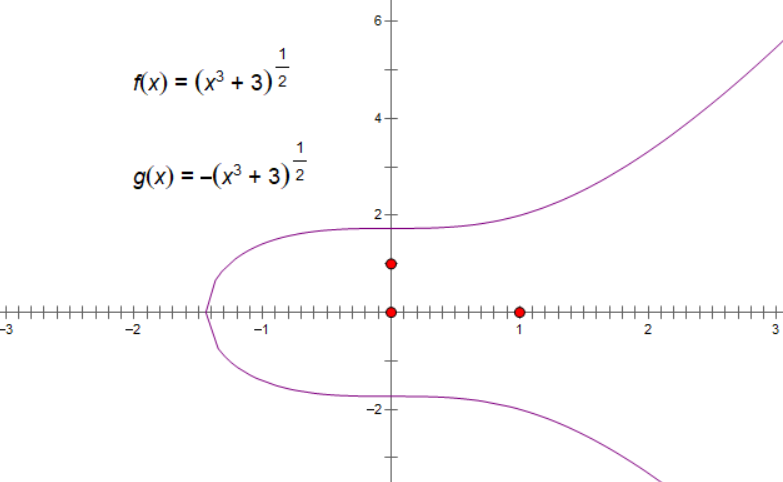
通过方程我们画出了曲线的图像,但是说这就是椭圆曲线的图像其实并不准确。
准确地说,我们画的是在实数域上这个方程的图像。在复数域上当然有更多的点也满足曲线方程但是我们的图像中并没有体现,例如 (-2, √5i) 。如果把曲线看作点的集合,那数域的扩张直接影响到我们要讨论的这个集合的大小,这在本文后半部分我们还会看到。
不懂复数也没关系,后面不会再提到。
另外为了让其拥有更多的性质,我们认为椭圆曲线其实还包括一个 “无穷远” 点。这个点在图中并不能体现出来,我们也不能以直角坐标的形式写出这个点的坐标,但是当我们说椭圆曲线时默认其点的集合中包含这个点。“无穷远” 点一般用 “O” 表示。
所谓的 “无穷远” 点更多是一个服务于概念的点,我们不能也不需要用坐标表示出来。
2 点的运算
有了 “元素的集合” 还需要有 “在集合上的运算”。
椭圆曲线上的点(有无穷个)就是椭圆曲线 “元素的集合”,但是为了构建密码算法还需要定义点的运算。这里我们只需要定义一种特殊的基本运算就可以,不妨将这种运算称作 “加法”,用 “+” 表示。
个人理解:把这里的 “定义一个运算” 理解为小学做的定义新运算就行了。
通过几何意义可以清楚地理解这种运算的定义,例如我们选取了曲线上的两个点 A 和 B 计算加法,把 A+B 的结果记为 C,过程如下:
- 过 A 点、B 点做直线,交曲线于 T 点;
- 过 T 点做 x 轴的垂线,交曲线于 C 点,C 点即为所求;
如下图所示:
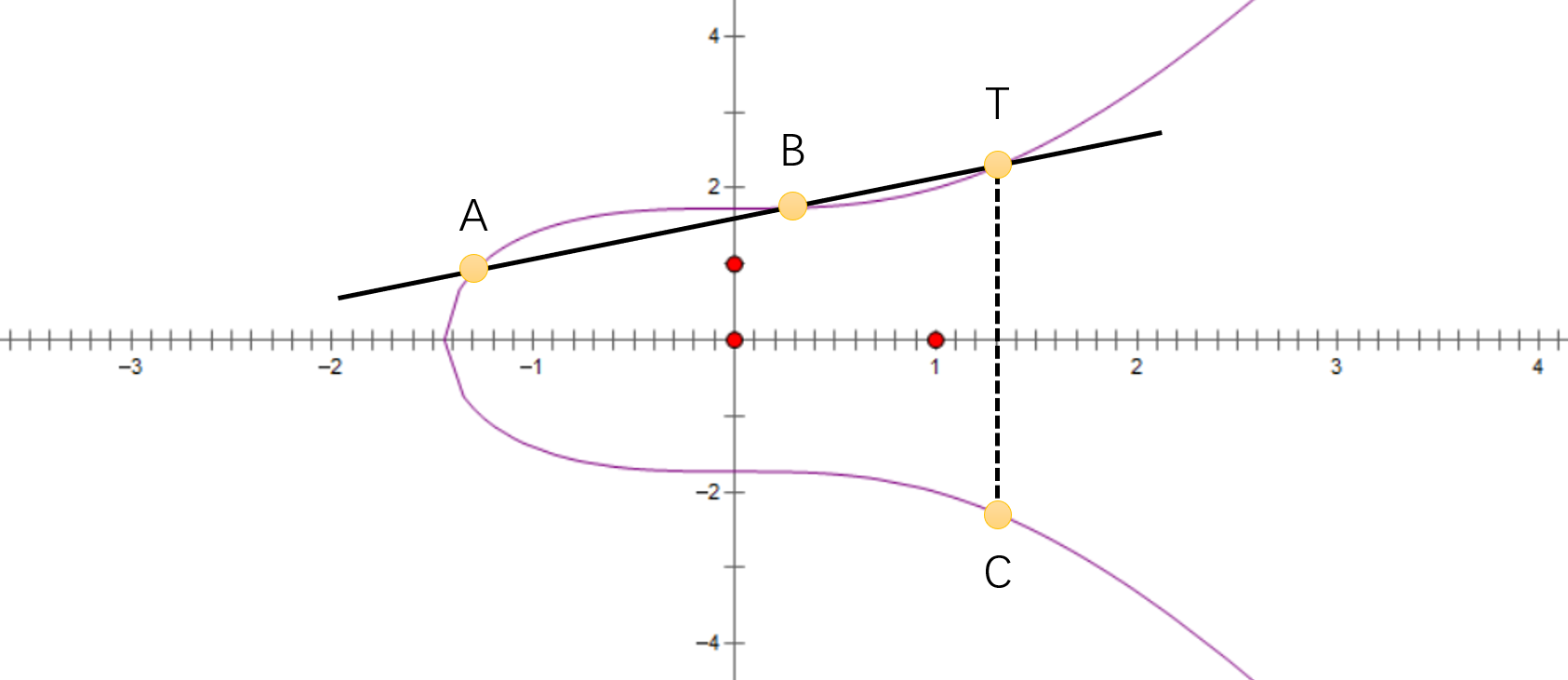
回忆:密码学 | 椭圆曲线 ECC 密码学入门(二)中作者比喻的台球运动。
需要说明的是:
① 当两个 “加数” 位置的点(即 A 点和 B 点)为同一个点时,上述步骤 1 中所做的,其实是过该点的 切线。

② 当 A 点、B 点的连线垂直于 x 轴时,我们规定直线 AB 和曲线的第三个交点(即除 A 点、B 点外的第三个交点)是 无穷远点 “O” 。
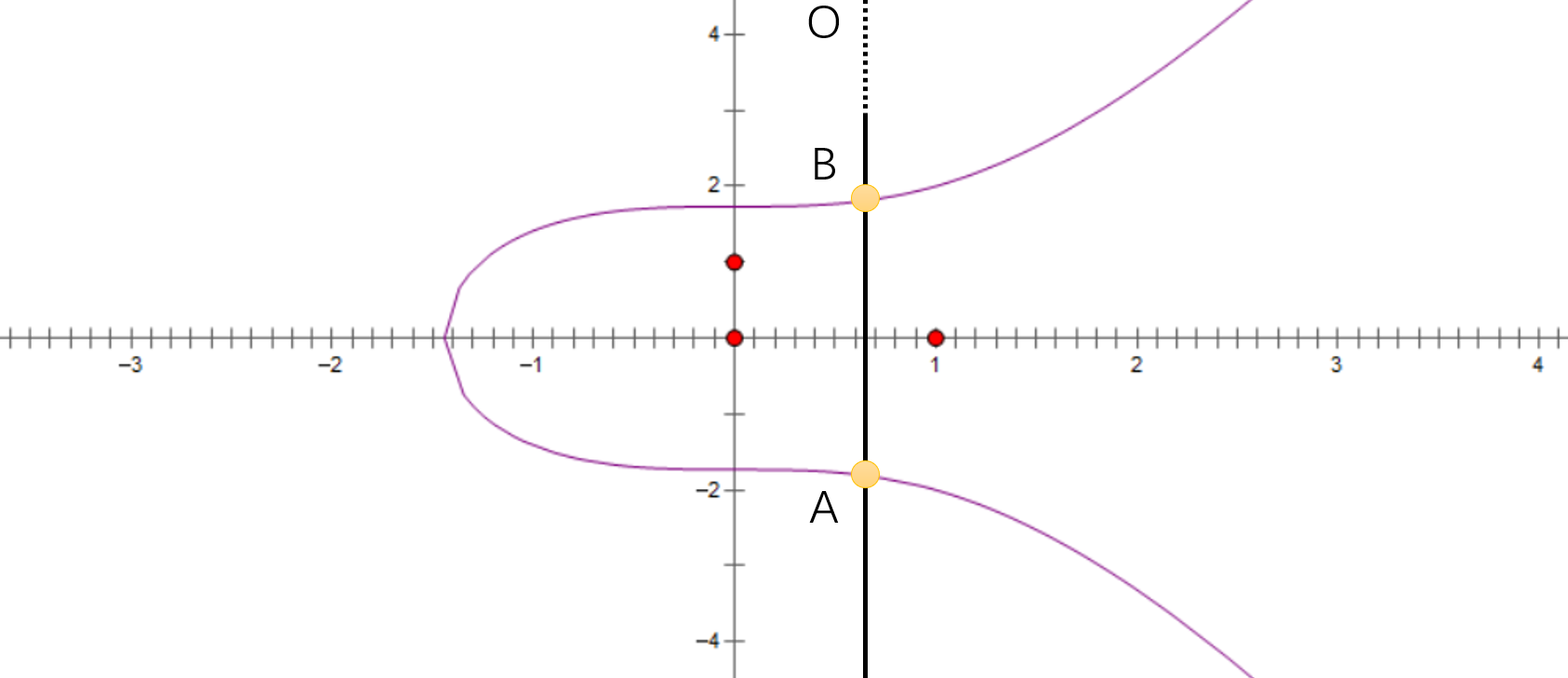
在这样的规则下容易发现:
- 任何 P 点都有一个对应的 P’ 点,使得 P+P’=O;
- 任何 A 点和 O 点的运算的结果都是 A 点本身;
- 由于连线 AB 和连线 BA 其实是同一条直线,因此这里定义的点的加法满足交换率。
针对第一条,P 和 P' 本质上说的就是 P 点和自己的对称点,即任何点及其对称点做 “加法” 都等于 O;针对第二条,将 A 点和 O 点连线,一定交曲线于 O 点本身,再过 O 点作垂线,又交于 A 点本身;针对第三条,也就是说 A+B=B+A=C 。
3 求解过程
根据定义再结合一些解析几何的知识,就可以求出 “点加法” 的坐标计算公式。
很遗憾,以我上大学后的知识水平是解不出来的。
假设椭圆曲线的方程为:
需要计算 A+B=C 这一过程中的坐标公式。
假设 A 点和 B 点的坐标分别为 (x_a, y_a) 和 (x_b, y_b),则 C 点的坐标如下:
其中 λ 是直线 AB 的斜率:
特别地,当 A、B 重合时,λ 是过 A 点的切线斜率:
就是椭圆曲线方程的等号两边同时求导再相除。
上述公式是没有问题的,的确是要代入 x_c 的值来求 y_c 的值。
现在我们将转而讨论 有限域 上的椭圆曲线,其上的椭圆曲线表现为一些散布的点。在有限域上,A+B 虽然已经没有明确的几何意义,但是有同样的计算公式。
我们已经验证过 (1, 2) 是椭圆曲线上的点,那么我们就把该点记为 G,并且从该点开始,计算 G、G+G、G+G+G…… 看看会有怎样的规律。
以 G+G 为例,我们进行演算,首先计算 λ,也就是 G 点(切线)的斜率:
为什么是 G 点切线的斜率?答:G+G 就等价于 A 点和 B 点重合的情况,因为 A 点是 G 点,B 点也是 G 点。为什么 4^{-1} 一下子变成了 76?答:因为这里使用了 “模乘法逆元”,属于是一个数学知识😇
然后计算 C 点坐标:
因此 G+G 的坐标为 (68, 74)。
就是把 G 点的坐标 (1, 2) 和斜率 λ 代入进去。
而 2G+G 稍稍有不同,主要是 λ 需要从切线斜率修改为直线 AB 的斜率:
同样地,代入公式计算 2G+G 的坐标:
因此我们也计算出 2G+G=3G 的坐标 (26, 45),以此类推进行计算,我们得到下表:
| 0 | O | 1 | (1, 2) | 2 | (68, 74) | 3 | (26, 45) | 4 | (65, 98) |
| 5 | (12, 32) | 6 | (32, 42) | 7 | (91, 35) | 8 | (18, 49) | 9 | (18, 52) |
| 10 | (91, 66) | 11 | (32, 59) | 12 | (12, 69) | 13 | (65, 3) | 14 | (26, 56) |
| 15 | (68, 27) | 16 | (1, 99) | 17 | O |
读者可以选择表中的点,例如 (32, 42),来验证其是否在曲线上,相关演算我们不在本文赘述。
接着,我们展示 17 个点在直角坐标系中的分布(无法展现 O),读者可以体会其中的对称之美:
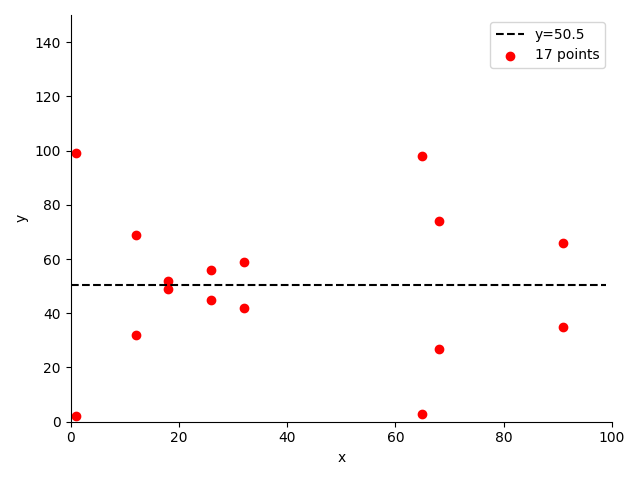
可能会好奇 16G+G 的结果到底是多少,以至于能称之为无穷点 O 点。个人认为,无穷点就是一个服务于 “模” 和 “循环” 这一概念的点,不能也不需要用坐标表示出来。
经过计算和验证可以发现,这一系列点构成了一个周期为 17 的循环。如果我们将 k 个 G 相加记为kG,并且将 O 看作 0G,同时定义 17G=O 。这像极了模 17 加法的规律,并且在模 17 加法和为 0 的两个数(即 0 和 17)对应的两个椭圆曲线点的和正好是 O 。
个人理解:“模 17 加法” 就是指,从 0 一直加一加到 17,再加一的话又回到 0 。
我们说这样的 17 个点和加法一起构成一个 有 17 个元素的循环群。
因为这只是一篇科普性质的文章,我们不给出 循环群 的严格定义,但是正如它的名字中强调的 “循环”,循环群 最突出的性质就是能够由某个元素不断运算从而得到全部。
需要强调的是这 17 个点并不是 F_{101} 上椭圆曲线的全部,但仅利用这 17 个元素组成的集合我们已经能够在其中完成点的加法运算,也就是说任意选择集合中两个点进行加法,其结果不会跳出到集合之外。
4 补充:有限域
域(Field)的定义是有如下特性的集合:
- 定义了加法和乘法;
- 集合里的元素经过加法和乘法计算,结果仍然在集合内;
- 计算符合交换率、结合率、分配率;
- 加法和乘法都有单位元素(集合里的值都有负数,集合里的非零值都有倒数);
举个例子,我们常见的实数集是域,但整数值不是域,这是因为除了 1,其它数的倒数都不是整数。特别地,具有有限个元素的域就是 有限域。
个人理解:不严格地来说,上述 17 个点构成的集合是一个有限域,因为集合里的元素经过 “加法” 计算,结果仍然在集合内。同时,“加法” 计算满足交换律。前文讲述的循环群只是一个加法循环群,事实上应该还有乘法循环群。