状态空间法
状态空间:一个问题全部可能的状态以及其关系的集合。
状态空间图:以图的形式表示问题的状态空间,节点对应状态,边对应状态转移算子,边上的权对应转移所需的代价
问题的解:是从最开始状态到目标状态的一条路径。
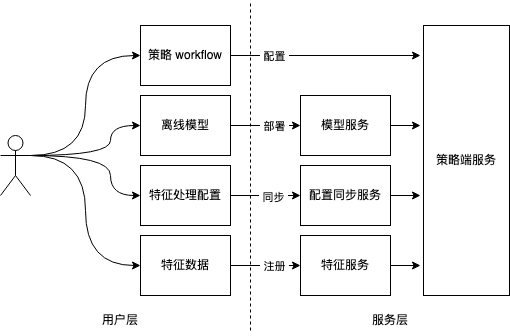
状态空间法就是将问题抽象为图:
状态->节点
操作->边
状态空间->图
问题的解->路径
求解过程->寻找路径
如:求三个硬币,一次翻两个,能否使三枚初始状态为数字面向上的硬币最终变为三枚国徽面向上的硬币。
我们可以枚举出三枚硬币可可能出现的全部8种状态,记数字面全部向上的状态为0,国徽面全部向上的状态为7,观察0节点是否能根据规则达到7节点。
图的搜索算法
通用图搜索算法
将所有节点分为三类:未知节点、已知已扩展节点(closed)、已知未扩展节点(open)
每次从open表中取一个节点N进行扩展,将扩展出来的新节点加入open表。结束后这个被选取的节点N加入closed表。
已扩展节点表为空还没找到目标节点,则问题无解.
状态空间图的分类
显式图:把状态空间图的全部要素(问题相关的全部状态、状态之间的关系)都以显式的像是存入知识库。
隐式图:初始时只存储初始状态,目标状态,状态之间的转移规则等信息。求解过程中,由初始状态出发,根据状态转移规则逐步生成所需的部分状态空间图。
状态空间图的计算机表示
Node.state 节点状态 Node.father 父节点指针 Node.g 历史已用代价
盲目搜索策略
广搜-open表为FIFO表
- 有解则一定能找到解
- 在单位耗散值的条件下,且问题有解,能找到最优解
- 方法与问题无关,具有通用性
- 效率低
深搜-open表为FILO表
- 一般不能保证找到最优解
- 当深度限制不合理时,可能找不到解
- 最坏情况,搜索空间等同于穷举
- 方法与问题无关,具有通用性
启发式搜索策略
对open表中的节点代价进行评估,选取代价最小的点进行扩展 f(n)=g(n)+h(n) g(n)已用代价 h(n)启发函数 代价优先(一致代价)搜索:只考虑g(n),令h(n)为0 爬山法(贪婪法):只考虑h(n)
A*算法h(n)<=h*(n)
- 算法可纳(有解问题,总能找到最优解)
- 在保证h(n)M=h*(n)的前提下,h(n)越大越好,h(n)越能准确的估计实际最小代价
评估函数的单调性
- 单调性(节点对(i,j),j为i的后继,评估函数对于所有的这种节点对都满足f(i)<=f(j))
博弈树搜索
博弈树适用于双方对弈的层次结构
使用Max表示本方,Min表示对方
最大最小法
原理
- 扩展当前棋局的全部N层子节点
- 确定各子节点评估值
- 最底层节点静态评估
- 其余子节点苹果汁需要逐层交替倒推(Max节点取最大值,Min节点取最小值)
步骤
- 生成规定深度的全部博弈树
- 计算所有最底层节点的静态估计函数值
- 自底向上逐层计算非终结节点的倒推估计值
- Max取最大,Min取最小
α-β剪枝
由于博弈树规模巨大,构造完整的博弈树需要消耗大量时间和内存
- 对于Max父节点,先探明的子节点可为父节点取值提供下界信息(α),小于α的未探明子节点可以忽略
- 对于Min父节点,先探明的子节点可为父节点取值提供上界信息(β),大于β的未探明字节的可以忽略
α剪枝:α父≥β β剪枝:α≥β父
- 跨层比较
- 有界深搜生成博弈树
剪枝演示
下图中我们看嘴左边的分支,由于MIN会选取评估值最小的节点,所以我们可以知道在这个节点的评估值为-3
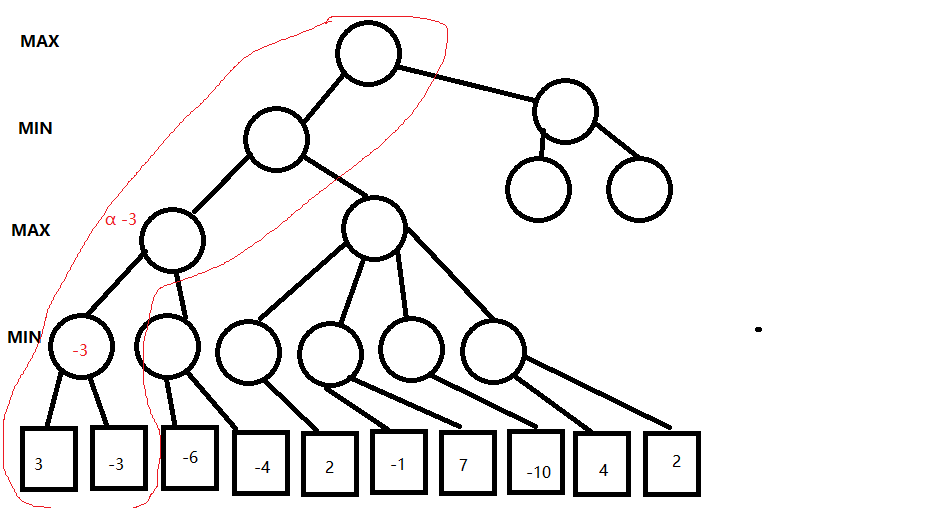
下图中,我们在右边第一个节点中找到了一个评估值为-6的节点,表示如果MAX选中这个分支,可以获得的最高得分只有-6(MIN会选择评估值最小的节点),-6<另一个分支的评估值-3,所以不需要评估后面的分支,我们就可以知道如果走这个分支我们最高只能获得-3分
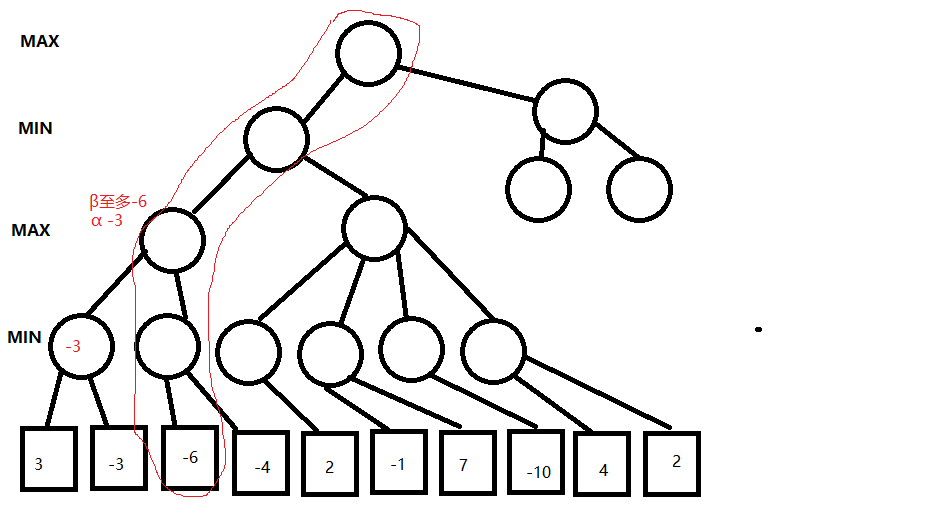
再看另一边,这边我们找到的第一个节点就是两分,由于MAX会倾向于获取高分这个分支的分数最低为2
所以对于MIN来说,选择这个分支的收益比选择前面那个-3的分支的收益低。
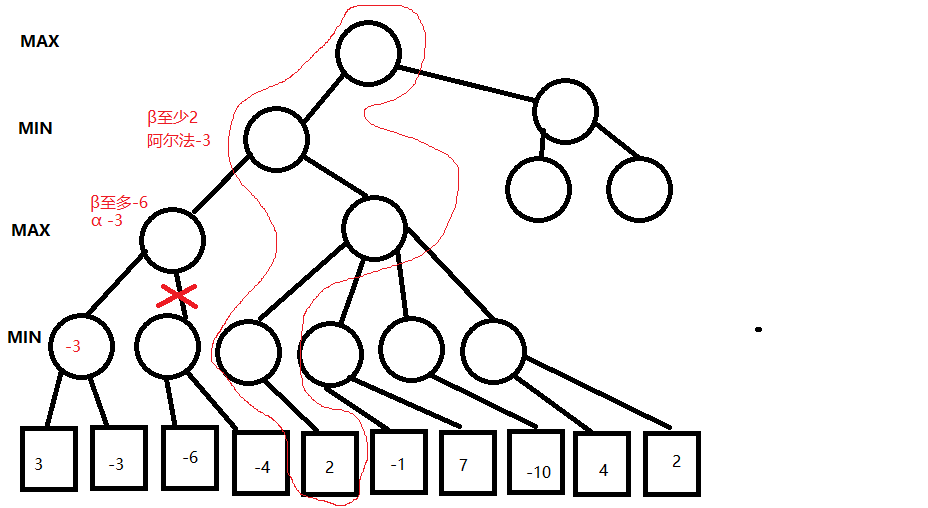
后面的节点都不需要再评估了
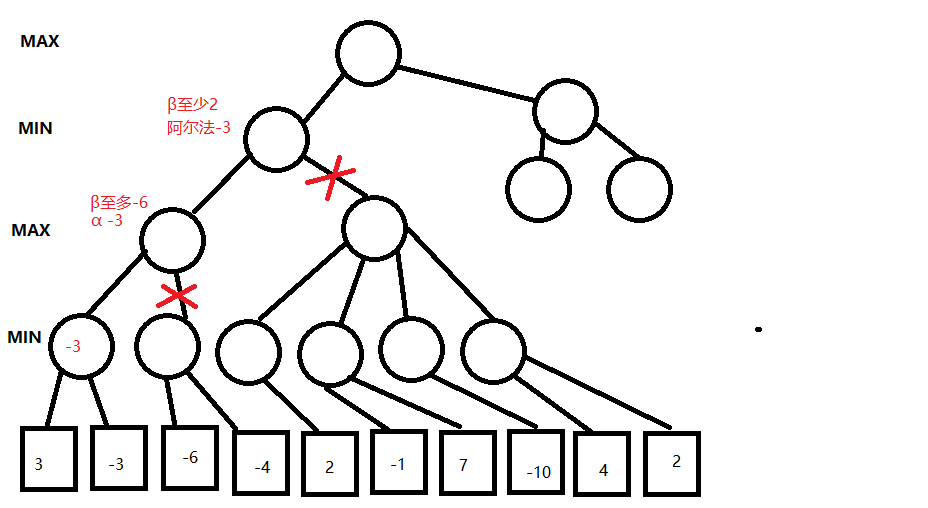
由此我们省去了6个节点的评估的时间,并且只进行了4次评估就做出了选择。