文章目录

• 1、N皇后
• 2、有效的数独
• 3、解数独
• 4、单词搜索
• 5、黄金矿工

1、N皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
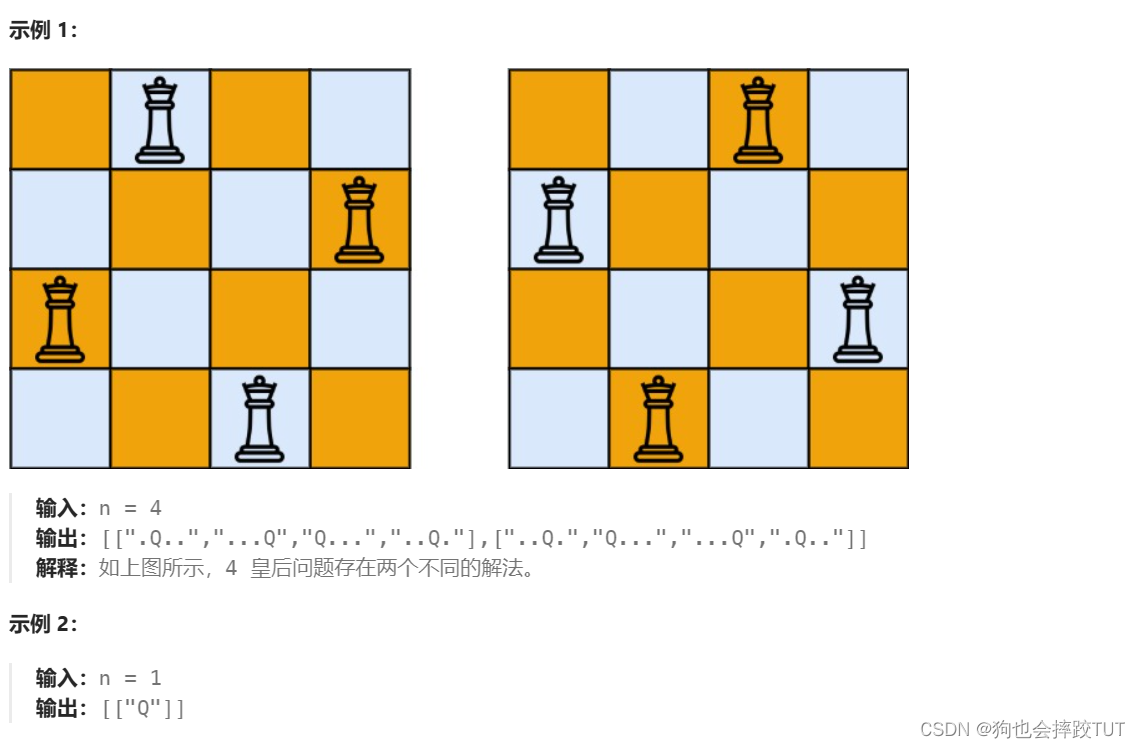
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

class Solution {
public:
    bool checkcol[10];//列           //剪枝
    bool dig1[20];//主 y-x+n=b+n     //剪枝
    bool dig2[20];//副 y+x+n=b+n     //剪枝
    vector<string> path;
    vector<vector<string>> ret;
    int n;

    vector<vector<string>> solveNQueens(int _n) {
        n=_n;
        path.resize(n);
        for(int i=0;i<n;i++)
            path[i].append(n,'.');
        dfs(0);
        return ret;
    }

    void dfs(int row)
    {
        if(row==n)
        {
            ret.push_back(path);
            return;
        }

        for(int col=0;col<n;col++)
        {
            if(checkcol[col]==false&&dig1[col-row+n]==false&&dig2[col+row]==false)
            {
                checkcol[col]=dig1[col-row+n]=dig2[col+row]=true;
                path[row][col]='Q';
                dfs(row+1);
                path[row][col]='.';
                checkcol[col]=dig1[col-row+n]=dig2[col+row]=false;
            }
        }
    }
};

2、有效的数独

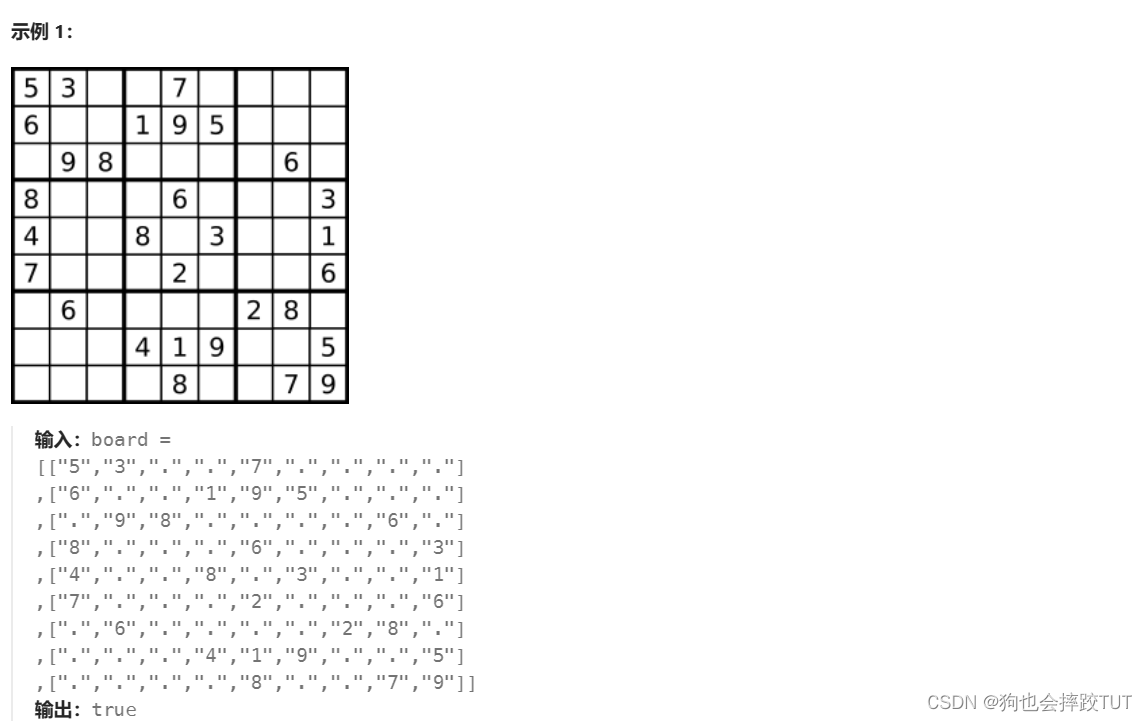
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
注意：
一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 ‘.’ 表示。

class Solution {
public:
    bool row[9][10];//横坐标代表第几行，纵坐标代表第i行是否有该数（就是纵坐标的下标）
    bool col[9][10];
    bool grid[3][3][10];
    bool isValidSudoku(vector<vector<char>>& board) {
        for(int i=0;i<9;i++)
        {
            for(int j=0;j<9;j++)
            {
                if(board[i][j]!='.')
                {
                    int num=board[i][j]-'0';
                    if(row[i][num]||col[j][num]||grid[i/3][j/3][num])
                        return false;
                    row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;
                }
            }
        }
        return true;
    }
};

3、解数独

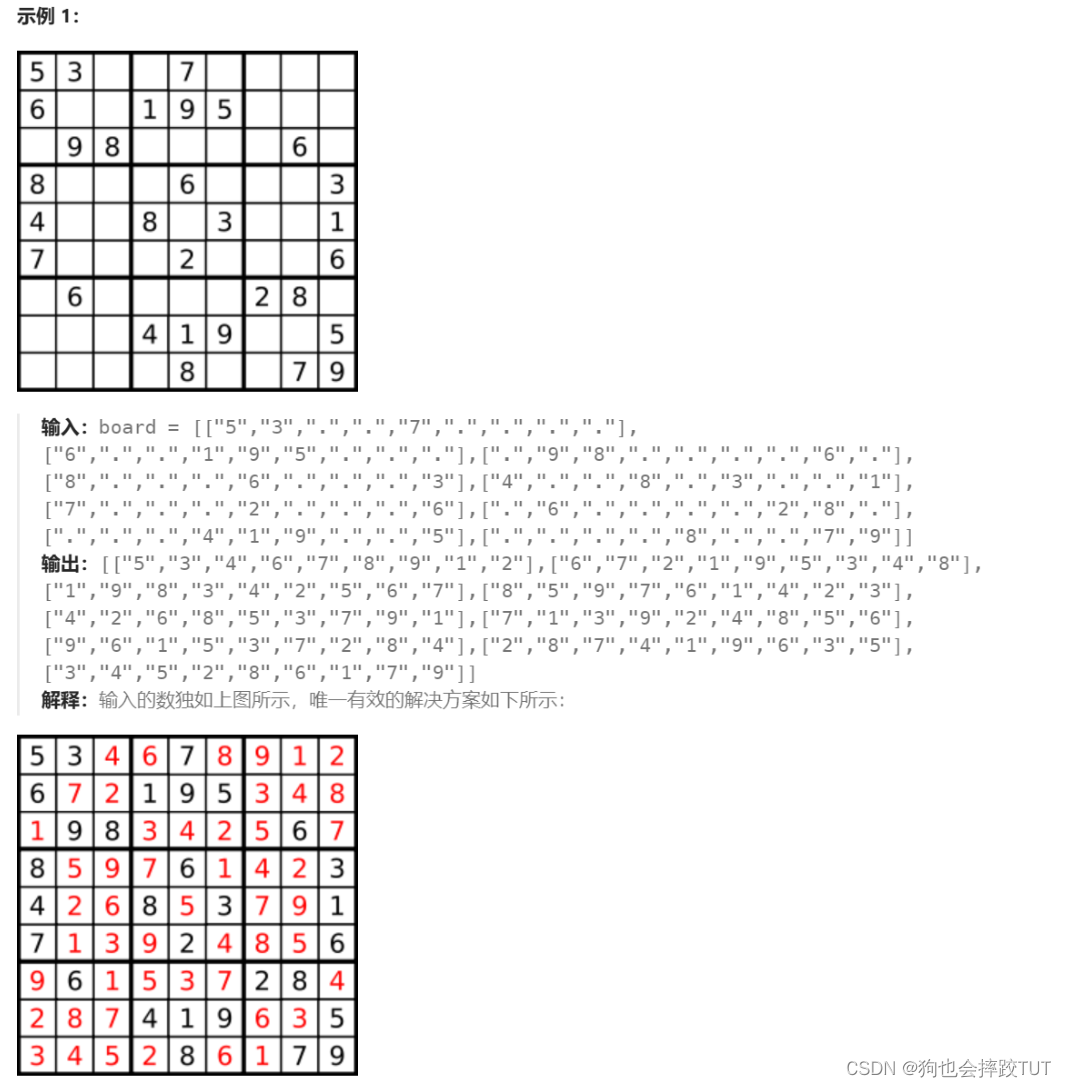
编写一个程序，通过填充空格来解决数独问题。
数独的解法需 遵循如下规则：
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

class Solution {
public:
    bool row[9][10];//横坐标代表第几行，纵坐标代表第i行是否有该数（就是纵坐标的下标）
    bool col[9][10];
    bool grid[3][3][10];
    void solveSudoku(vector<vector<char>>& board) {
        for(int i=0;i<9;i++)
        {
            for(int j=0;j<9;j++)
            {
                if(board[i][j]!='.')
                {
                    int num=board[i][j]-'0';
                    row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;
                }
            }
        }
        dfs(board);
    }

    bool dfs(vector<vector<char>>& board)
    {
        for(int i=0;i<9;i++)
        {
            for(int j=0;j<9;j++)
            {
                if(board[i][j]=='.')
                {
                    for(int num=1;num<10;num++)
                    {
                        if(row[i][num]==false&&col[j][num]==false&&grid[i/3][j/3][num]==false)
                        {
                            board[i][j]='0'+num;
                            row[i][num]=col[j][num]=grid[i/3][j/3][num]=true;
                            if(dfs(board)==true) return true;
                            board[i][j]='.';
                            row[i][num]=col[j][num]=grid[i/3][j/3][num]=false;
                        }
                    }
                    return false;//就说明1-9没有一个合适的，就需要向上返回换一种方式
                }
            }
        }//通过两层循环遍历，到这里就是已经填满了，所以就可以返回了
        return true;
    }
};

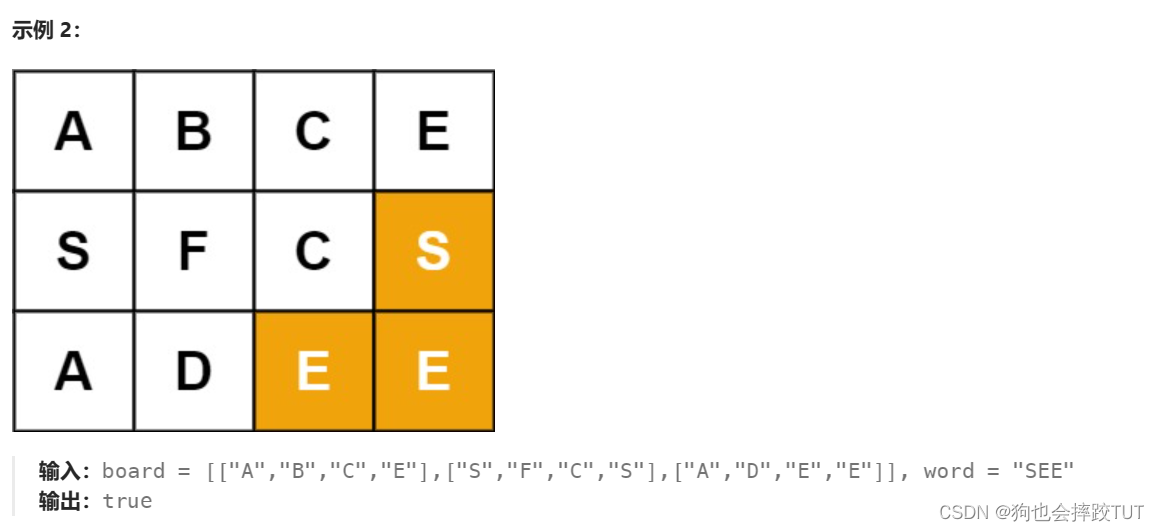
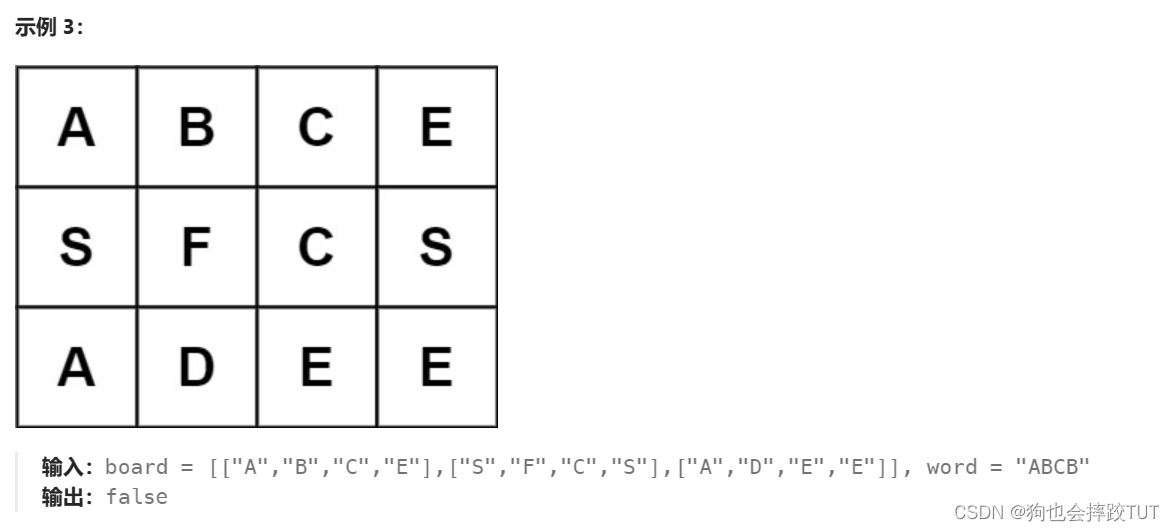
4、单词搜索

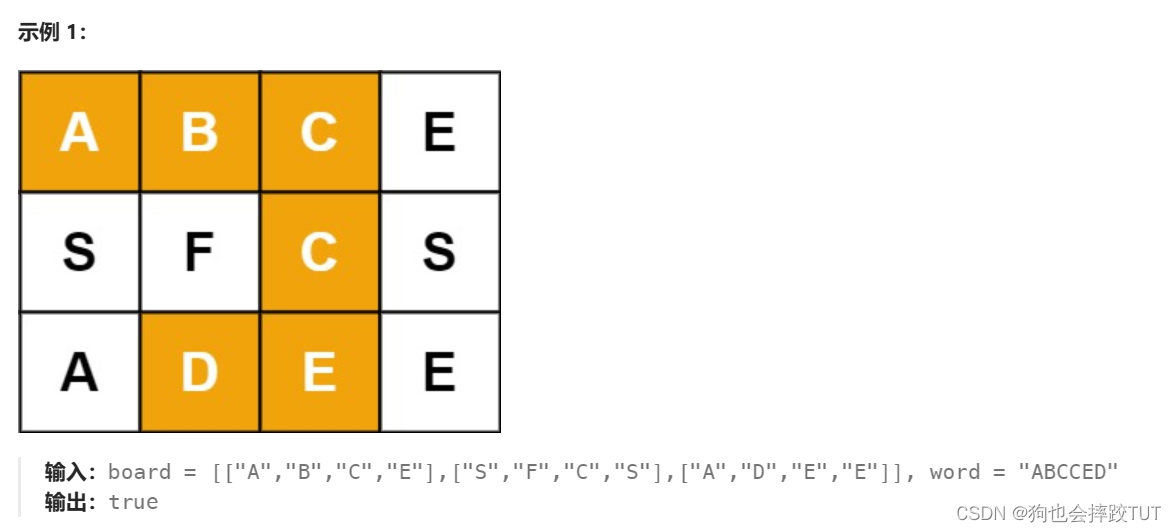
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

class Solution {
public:
    int flag[7][7];
    int n,m;
    bool exist(vector<vector<char>>& board, string word) {
        n=board.size();
        m=board[0].size();
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(board[i][j]==word[0])
                {
                    flag[i][j]=true;
                    if(dfs(board,i,j,word,1)) return true;
                    flag[i][j]=false;
                }
            }
        }
        return false;
    }

    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};

    bool dfs(vector<vector<char>>& board,int i,int j,string &word,int pos)
    {
        if(pos==word.size())
            return true;
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k];
            int y=j+dy[k];
            if(x>=0 && x<n && y>=0 && y<m && flag[x][y]==false && board[x][y]==word[pos])
            {
                flag[x][y]=true;
                if(dfs(board,x,y,word,pos+1)) return true;
                flag[x][y]=false;
            }
        }
        return false;
    }
};

5、黄金矿工

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。
为了使收益最大化，矿工需要按以下规则来开采黄金：
每当矿工进入一个单元，就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采（进入）一次。
不得开采（进入）黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

class Solution {
public:
    bool flag[16][16];
    int maxsum;
    int n,m;
    int getMaximumGold(vector<vector<int>>& grid) {
        n=grid.size();
        m=grid[0].size();
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(grid[i][j]!=0)
                {
                    flag[i][j]=true;
                    dfs(grid,i,j,0+grid[i][j]);
                    flag[i][j]=false;
                }
            }
        }
        return maxsum;
    }

    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};

    void dfs(vector<vector<int>>& grid,int i,int j,int sum)
    {
        maxsum=max(maxsum,sum);
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k];
            int y=j+dy[k];
            if(x>=0 && x<n && y>=0 && y<m &&grid[x][y]!=0&&flag[x][y]==false)
            {
                flag[x][y]=true;
                dfs(grid,x,y,sum+grid[x][y]);
                flag[x][y]=false;
            }
        }
    }
};