最小生成树算法的实现c++
题目链接:1584. 连接所有点的最小费用 - 力扣(LeetCode)
主要思路:使用krusal算法,将边的权值进行排序(从小到大排序),每次将权值最小且未加入到连通分量中的值给加入其中。主要需要使用并查集,检查是否在同一个连通分量当中。
class Solution {
public:
typedef struct edge{
int id; //表示这个点
int to; //表示要到达的点
int weight;//权重
bool operator<(edge a) const{
return a.weight>weight;
}
}edge;
int calcute(vector<int> point1,vector<int> point2)
{
return abs(point1[0]-point2[0])+abs(point1[1]-point2[1]);
}
int find(int u,vector<int>& parents)
{
if(parents[u]==u)
{
return u;
}
else
{
return find(parents[u],parents);
}
}
int find(int u,vector<int>& parents) //路径压缩后的
{
while(u!=parents[u])
{
parents[u]=parents[parents[u]];
u=parents[u];
}
return u;
}
/*bool is_same_parent(int u,int v)
{
if(find(u)==find(v))
{
return true;
}
return false;
}*/
int minCostConnectPoints(vector<vector<int>>& points) {
int n=points.size();
vector<edge> edges;
// vector<bool> is_valid(n,false);
vector<int> parents(n,0);
for(int i=0;i<n;i++)
{
parents[i]=i;
}
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
edge temp1;
temp1.id=i;
temp1.to=j;
temp1.weight=calcute(points[i],points[j]);
// edge temp2;
// temp2=temp1;
// temp2.id=temp1.to;
// temp2.to = temp1.id;
edges.push_back(temp1);
// edges.push_back(temp2);
}
}
sort(edges.begin(),edges.end());
int count=0;
int ans=0;
// is_valid[edges[0].id]=true;
for(int i=0;i<edges.size();i++)
{
int parent1=find(edges[i].id,parents);
int parent2=find(edges[i].to,parents);
if(parent1!=parent2)
{
parents[parent2]=parent1;
cout<<"取边"<<edges[i].id<<"-"<<edges[i].to<<"权重为:"<<edges[i].weight<<endl;
ans+=edges[i].weight;
count++;
}
if(count==n)
{
break;
}
}
return ans;
/*for(int i=0;i<edges.size();i++)
{
cout<<"本点:"<<edges[i].id<<"要到达的点:"<<edges[i].to<<"权重为:"<<edges[i].weight<<endl;
}
return 0;*/
}
};
使用prime算法做最小生成树
首先要了解什么是链式前向星
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,
并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.
用len[i]来记录所有以i为起点的边在数组中的存储长度.
用head[i]记录以i为边集在数组中的第一个存储位置.
在这里插入图片描述
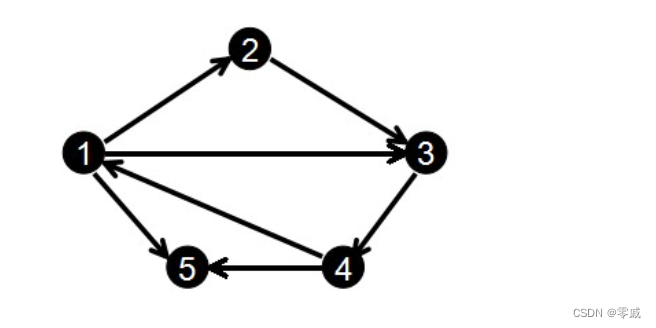

用链式前向星可以避开排序,建立边结构体
struct Edge{
int next;
int to; //edge[i].to表示第i条边的重点,edge[i].next表示与第i条边同起点的下一条边的存储位置
int weight;//边的权值
}
另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实
在以i为起点的所有边的最后输入的那个编号.
加边函数为
void add(int u,int v,int w)
{
edge[cnt].w = w;
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}


#include <bits/stdc++.h>
#define INF 0x7f7ff
using namespace std;
int k; //默认初始为0
int head[5010];//由于节点最多为5000个,初始化nodes[i]=0,node[i]表示以第i个节点为起始点第一次出现的位置
struct node{
int to;
int weight;
int next;
}edges[400010];//由于是无向图,要开两倍数组
int n,m;
int ans;
bool vis[5010];//代表该节点是否被访问
int dist[5010];//dis[i]表示已经加入到最小生成树的点到没有加入的点的最短距离
void add(int u,int to,int weight) //实际是逆序的,但不影响结果的正确性,在此使用的是链式前向星,不理解链式前向星的去搜一下前向星相关内容
{
edges[++k].to= to;
edges[k].weight=weight;
edges[k].next = head[u];
head[u]=k;
}
void prime()
{
fill(dist+1,dist+n+1,INF);
dist[1]=0;//选择起点为1
for(int i=1;i<=n;i++)
{
int u=-1,minn=INF;
for(int j=1;j<=n;j++)
{
if(dist[j]<minn&&!vis[j]) //将距离进行更改,且该点要未被访问
{
u=j;
minn=dist[j]; //更新min值
}
}
if(u==-1)
{
ans=-1;
return;
}
vis[u]=true;
ans+=dist[u];
for(int j=head[u];j;j=edges[j].next)
{
int v=edges[j].to;
if(!vis[v]&&dist[v]>edges[j].weight) dist[v]=edges[j].weight;
}
}
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++) //建立
{
int from,to,weight;
cin>>from>>to>>weight;
add(from,to,weight);
add(to,from,weight);
}
prime();
if(ans==-1)
{
cout<<"orz"<<endl;
}
else
{
cout<<ans<<endl;
}
//cout<<edges[0].from<<"-"<<edges[0].to<<"-"<<edges[0].weight<<endl;
//cout<<edges[1].from<<"-"<<edges[1].to<<"-"<<edges[1].weight<<endl;
// 请在此输入您的代码
return 0;
}
由于每次枚举dist比较花费时间,因此可以对其进行优化,使用priority_queue来找最短的距离
struct p
{
int id,d;
bool operator < (const p &a) const
{
return a.d<d;
}
};
void Prime()
{
fill(dist+1,dist+1+n,INF);
priority_queue<p> q;
p now;
now.id=1;now.d=dist[1]=0;
q.push(now);
while(!q.empty())
{
p now=q.top();q.pop();
int u=now.id;
if(now.d!=dist[u]) continue;
vis[u]=1;
ans+=dist[u];
tot++;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(!vis[v]&&dist[v]>edge[i].w)
{
dist[v]=edge[i].w;
p nxt;
nxt.d=dist[v];
nxt.id=v;
q.push(nxt);
}
}
}
if(tot<n) ans=-1;
}
if(!vis[v]&&dist[v]>edge[i].w)
{
dist[v]=edge[i].w;
p nxt;
nxt.d=dist[v];
nxt.id=v;
q.push(nxt);
}
}
}
if(tot<n) ans=-1;
}