数据结构|并查集

并查集

心有猛虎，细嗅蔷薇。你好朋友，这里是锅巴的C\C++学习笔记，常言道，不积跬步无以至千里，希望有朝一日我们积累的滴水可以击穿顽石。

有趣的并查集剧情演绎：【算法与数据结构】—— 并查集

并查集
并查集是一种关于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。
一般地，我们只关心树的根节点和树的大小。注意，并查集的最终修改与查询都是根节点，而不是父节点(fa)，父节点只是用来实现并查集的过程。因此，查询某个点属于哪个集合以及集合的大小，都是在根节点上进行操作，也就是find(x)，但不是fa[x]。

并查集

补充
如果题目中没有给权值，把模板中size部分删除即可

初始化

int fa[N],sz[N];//父节点father和大小size
    for(int i=1;i<=n;i++){
        fa[i] = i;
        sz[i] = 1;//sz表示带权并查集，初始可为1可不为1，视具体情况而定
    }

查询(路径压缩)

int find(int x){//之后再次查询时，时间复杂度为O（1）
    return fa[x] == x?x:fa[x]=find(fa[x]);
}

按秩合并

void merge(int x,int y){
    x = find(x),y=find(y);
    if(x!=y){
        if(sz[x]>sz[y]) swap(x,y);
        fa[x]=y;
        sz[y]+=sz[x];
    }
}
//实际上按秩合并不是必须的，实际上按秩合并完全可由路径压缩替代。因为路径压缩已经将时间复杂度降到了O(1)。

二维并查集

//只需一个hash映射，将二维映射到一维即可
for(int i=0;i<n;i++){
    for(int j=0;j<n;j++){
        fa[i*n+j] = i*n+j;
        sz[i*n+j] = 1;
    }
}

删除节点

int cnt=n-1;

for(int i=0;i<n;i++) real[i]=i;
    
void delete(int x){
    real[x]=++cnt;
    fa[real[x]]=real[x];
    x=find(x);
    sz[x]-=1;
}

例题
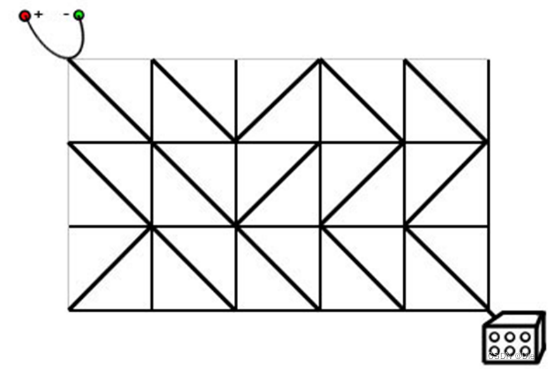
蓝桥杯2017国赛真题-合根植物

心有猛虎，细嗅蔷薇。再见了朋友~