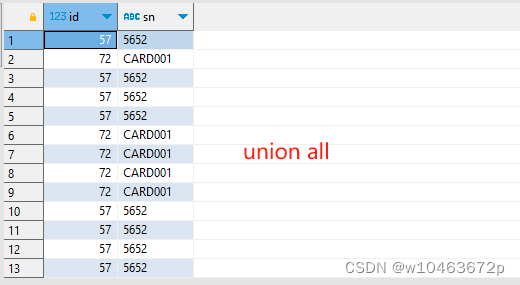
1、先回顾下熵值的数据公式:

2、jax.numpy代码
注意的点:熵值计算的输入的必须是归一化的正值
import jax.numpy as jnp
import jax
def _entroy(probs):
log_probs = jnp.log2(jnp.maximum(1.0e-30, probs))
mean_sum_plogp = jnp.mean(- jnp.sum(log_probs * probs, axis=-1))
return mean_sum_plogp
随机
key = jax.random.PRNGKey(123)
inputs = jax.random.normal(key, shape=(3, 4))
print(f'inputs:\n{inputs}')
probs1 = jax.nn.softmax(inputs)
print(f'probs1:\n{probs1}')
entroy_value1 = _entroy(probs1)
print(f'entroy_value1: {entroy_value1}\n\n')
输出:
inputs:
[[-0.31682462 -1.5700184 0.6431673 -0.11953171]
[ 0.21440512 -0.886306 -0.0515956 -0.81674606]
[-1.241783 -0.63905096 -0.65371424 0.88143796]]
probs1:
[[0.19548938 0.05583005 0.5105548 0.23812577]
[0.40722093 0.13545571 0.31210986 0.14521345]
[0.07700823 0.140702 0.1386539 0.64363587]]
entroy_value1: 1.6717370748519897
极端均匀
极端均匀,熵值最大。最大值为log2(dim),例子的shape为3 * 4,我们计算的为最后一维的熵值情况,因此dim为4,所以log2(4) = 2。
probs2 = jnp.array([[0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25]])
print(f'probs2:\n{probs2}')
entroy_value2 = _entroy(probs2)
print(f'entroy_value2: {entroy_value2}\n\n')
输出:
probs2:
[[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]]
entroy_value2: 2.0
增加混乱程度
增加混乱度,熵值减小
# 修改了矩阵的概率值
probs3 = jnp.array([[0.5, 0, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25]])
print(f'probs3:\n{probs3}')
entroy_value3 = _entroy(probs3)
print(f'entroy_value3: {entroy_value3}\n\n')
输出:
probs3:
[[0.5 0. 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]]
entroy_value3: 1.8333333730697632
极端混乱
极端混乱度,熵值最小,最小值跟矩阵的维度无关,基本都为0
probs4 = jnp.array([[0, 0, 1, 0],[0, 0, 1, 0], [0, 0, 1, 0]])
print(f'probs4:\n{probs4}')
entroy_value4 = _entroy(probs4)
print(f'entroy_value4: {entroy_value4}\n\n')
输出:
probs4:
[[0 0 1 0]
[0 0 1 0]
[0 0 1 0]]
entroy_value4: 0.0
3、numpy代码:
import numpy as np
剩下代码把随机输jnp换成np即可。然后就是生成随机输入和Softmax也有点不一样。
4、torch代码
import torch
def _entroy(probs):
log_probs = torch.log2(torch.maximum(torch.tensor(1.0e-30), probs))
mean_sum_plogp = torch.mean(- torch.sum(log_probs * probs, dim=-1))
return mean_sum_plogp
torch.manual_seed(123)
随机
inputs = torch.rand(3, 4)
print(f'inputs:\n{inputs}')
probs1 = torch.nn.functional.softmax(inputs)
print(f'probs1:\n{probs1}')
entroy_value1 = _entroy(probs1)
print(f'entroy_value1: {entroy_value1}\n\n')
输出:
inputs:
tensor([[0.2961, 0.5166, 0.2517, 0.6886],
[0.0740, 0.8665, 0.1366, 0.1025],
[0.1841, 0.7264, 0.3153, 0.6871]])
probs1:
tensor([[0.2135, 0.2662, 0.2042, 0.3161],
[0.1886, 0.4166, 0.2008, 0.1940],
[0.1814, 0.3120, 0.2068, 0.2999]])
entroy_value1: 1.947859764099121
极端均匀
probs2 = torch.tensor([[0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25]])
print(f'probs2:\n{probs2}')
entroy_value2 = _entroy(probs2)
print(f'entroy_value2: {entroy_value2}\n\n')
输出:
probs2:
tensor([[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]])
entroy_value2: 2.0
改变矩阵的混乱程度
probs3 = torch.tensor([[0.5, 0, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25]])
print(f'probs3:\n{probs3}')
entroy_value3 = _entroy(probs3)
print(f'entroy_value3: {entroy_value3}\n\n')
输出:
probs3:
tensor([[0.5000, 0.0000, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]])
entroy_value3: 1.8333333730697632
极端混乱
probs4 = torch.tensor([[0, 0, 1, 0],[0, 0, 1, 0], [0, 0, 1, 0]])
print(f'probs4:\n{probs4}')
entroy_value4 = _entroy(probs4)
print(f'entroy_value4: {entroy_value4}\n\n')
输出:
tensor([[0, 0, 1, 0],
[0, 0, 1, 0],
[0, 0, 1, 0]])
entroy_value4: 0.0