最近我在使用wordpress网站进行建站。 我是使用的hostease的主机产品进行wordpress建站,在选择wordpress主题时颇为头疼。后来咨询了hostease的客服人员,他们家的技术人员提供了诸多帮助。在WordPress网站建设时,主题选择对于建立各类网站至关重要。根据不同类型的网站需求,选择合适的主题能够为网站提供更好的外观和功能。在这篇文章中,我们将根据使用经验介绍几种常用的 WordPress 主题,并探讨它们的特点和适用场景。
个人博客和企业官网建站:
对于个人博客和企业官网建站,Astra 和 Kadence 主题是不错的选择。它们提供了丰富的定制选项,可以轻松地调整网站的外观和布局。从上传网站的 logo 到设置网站名称,这些主题都提供了方便的自定义功能,使用户可以快速搭建出令人满意的网站。
Astra
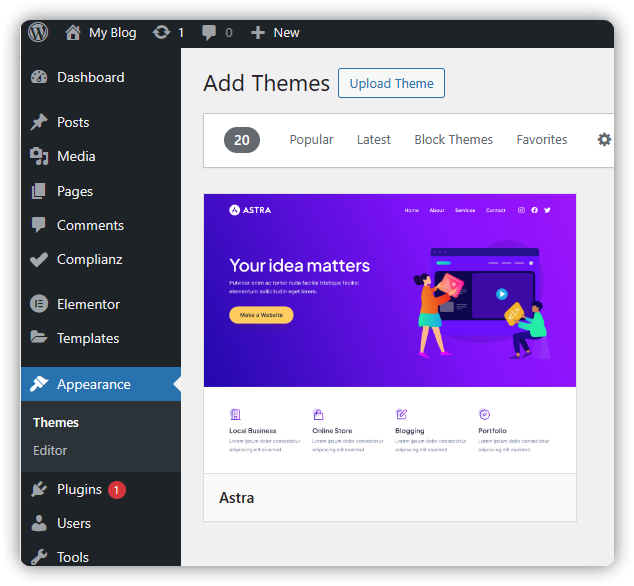
添加图片注释,不超过 140 字(可选)
Kadence
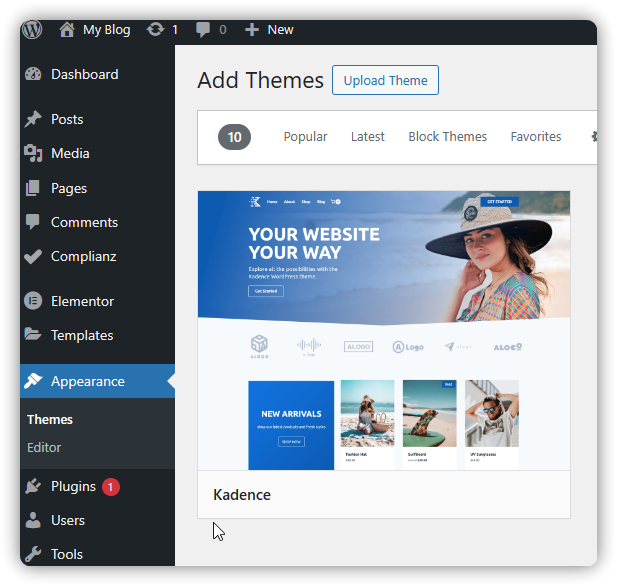
添加图片注释,不超过 140 字(可选)
B2C 建站:
如果您需要建立一个 B2C 网站,Woodmart 主题是一个理想的选择。它专注于电商功能,提供了许多与在线销售相关的特性和工具。Woodmart 主题不仅外观时尚,而且功能强大,适用于各种类型的电子商务平台。
DIY 建站:
对于喜欢自己动手搭建网站的用户,Hello Elementor 主题与 Elementor Pro 插件的组合是一个不错的选择。它们提供了直观的页面构建工具,让用户可以轻松地创建自己想要的布局和设计。通过简单拖放的方式,用户可以实现各种创意,打造独特的个人博客或网站。
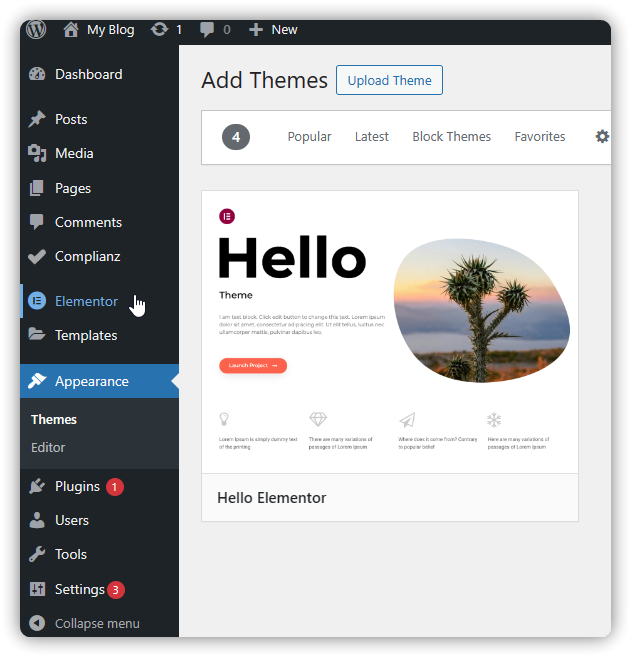
添加图片注释,不超过 140 字(可选)
在自定义配置方面,不同主题提供了不同的选项。一些主题将配置集成到 WordPress 的通用自定义菜单中,而另一些则提供了单独的设置页面。例如,Betheme 和 Astra 主题的自定义配置项展示了不同的功能选择,用户可以根据自己的需求进行调整。
除了主题自带的配置选项外,有些插件也会在自定义菜单中添加额外的功能。这些插件可以为网站提供更多的定制选项和增强功能,使用户可以更好地满足自己的需求。
综上所述,选择合适的 WordPress 主题并根据需求进行自定义配置是建立成功网站的关键。无论您是要建立个人博客、企业官网、B2C 网站还是 DIY 建站,都可以根据本文提供的建议找到最佳的解决方案,打造出令人印象深刻的网站。