7.5.1 散列表的基本概念

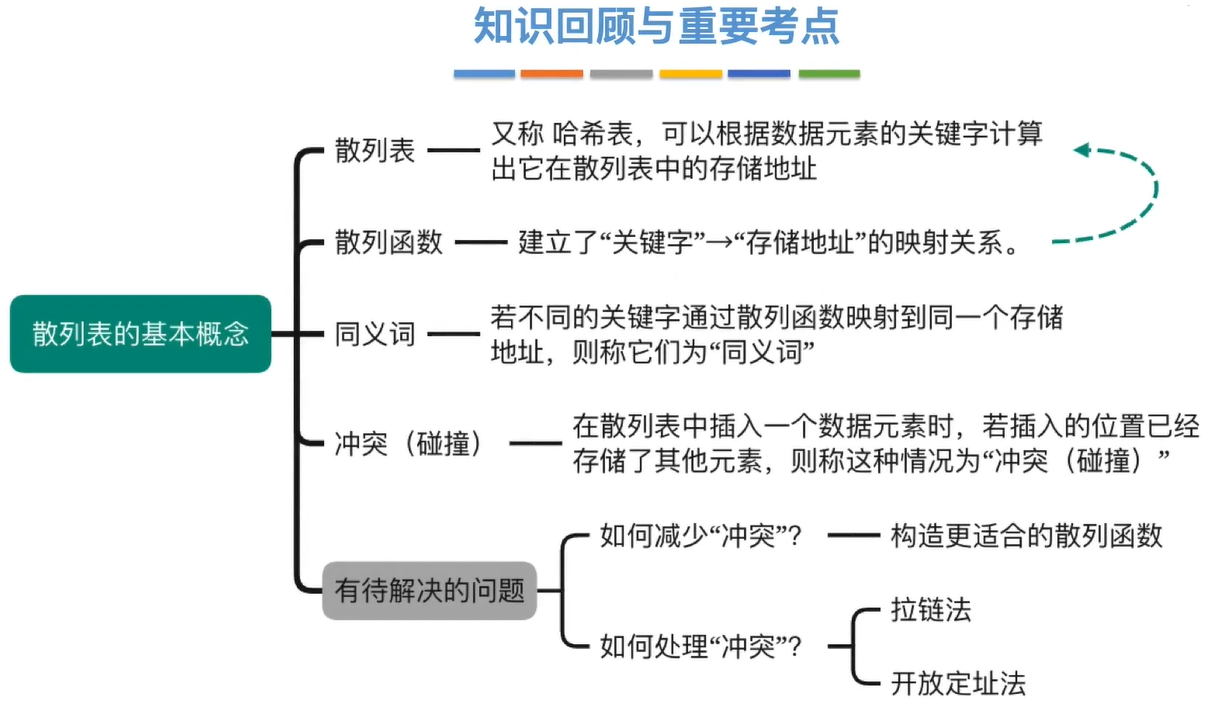
散列表（哈希表，Hash Table)︰是一种数据结构。特点是∶可以根据数据元素的关键字计算出它在散列表中的存储地址
散列函数（哈希函数)︰Addr=H(key)建立了“关键字”→“存储地址”的映射关系

冲突（碰撞)︰在散列表中插入一个数据元素时，需要根据关键字的值确定其存储地址，若该地址已经存储了其他元素，则称这种情况为“冲突(碰撞)”

同义词:若不同的关键字通过散列函数映射到同一个存储地址，则称它们为“同义词”

如何减少“冲突”？
对于散列函数 H(key)=key%13 来说，1 和 14 是“同义词”，可以构造更适合的散列函数，让各个关键字尽可能地映射到不同的存储位置,从而减少“冲突”

Eg:把散列函数改为H(key)=key%12，则不发生冲突
19%12=7
14%12=2
23%12=11
1%12=1

如何处理冲突？
拉链法(又称链接法、链地址法)︰把所有“同义词”存储在一个链表中。
开放定址法:如果发生“冲突”，就给新元素找另一个空闲位置。

7.5.2 散列函数的构造

散列函数（哈希函数)︰Addr=H(key)建立了“关键字”→“存储地址”的映射关系。

设计散列函数时应该注意：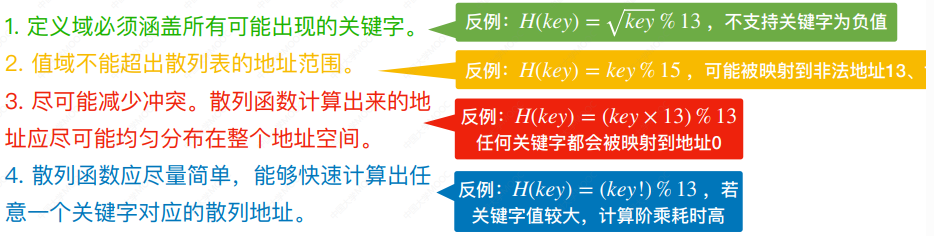

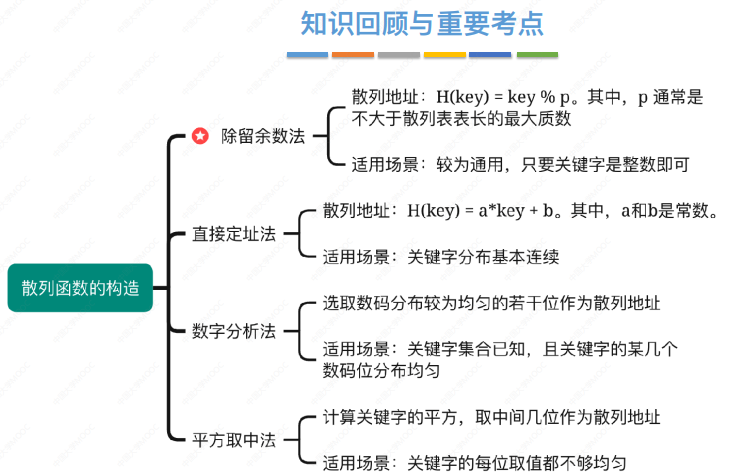
除留余数法——H(key) = key % p
散列表表长为m，取一个不大于m但最接近或等于m的质数p
注︰质数又称素数。指除了1和此整数自身外,不能被其他自然数整除的数
适用场景:较为通用，只要关键字是整数即可


拓展：为什么除留余数法要对质数取余？

直接定址法——H(key) = key或H(key) = a*key + b
其中，a和b是常数。这种方法计算最简单，且不会产生冲突。若关键字分布不连续，空位较多，则会造成存储空间的浪费。
适用场景:关键字分布基本连续

数字分析法——选取数码分布较为均匀的若干位作为散列地址
设关键字是r进制数〈如十进制数)，而r个数码在各位上出现的频率不一定相同，可能在某些位上分布均匀一些，每种数码出现的机会均等;而在某些位上分布不均匀，只有某几种数码经常出现，此时可选取数码分布较为均匀的若干位作为散列地址。
适用场景:关键字集合已知，且关键字的某几个数码位分布均匀。

平方取中法——取关键字的平方值的中间几位作为散列地址。
具体取多少位要视实际情况而定。这种方法得到的散列地址与关键字的每位都有关系，因此使得散列地址分布比较均匀。
适用场景:关键字的每位取值都不够均匀。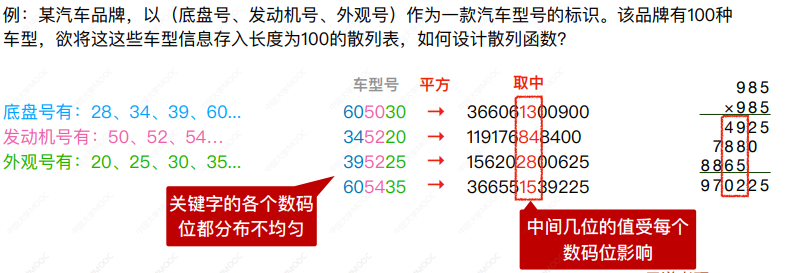

7.5.3_1 处理冲突的方法_拉链法

拉链法(又称链接法、链地址法)︰把所有“同义词”存储在一个链表中
如何在散列表(拉链法解决冲突)中插入一个新元素?
Step 1:结合散列函数计算新元素的散列地址
Step 2:将新元素插入散列地址对应的链表（可用头插法，也可用尾插法)

散列表的插⼊操作（拉链法解决冲突）

散列表的查找操作(拉链法解决冲突)

查找目标20，计算目标元素存储地址:20%13=7；  20查找成功，查找长度=1
查找目标66，计算目标元素存储地址:66%13=1；  66查找失败，查找长度=4
查找目标21，计算目标元素存储地址:21%13=8；  21查找失败，查找长度=0

查找长度——在查找运算中，需要对比关键字的次数称为查找长度.
注：有的教材会把“空指针的对比”也计入查找长度。但考试中默认只统计 “关键字对比次数”

散列表的删除操作(拉链法解决冲突)

删除目标：27 ，计算目标元素存储地址:27%13=1； 27查找成功，删除成功
删除目标：20 ，计算目标元素存储地址:20%13=7； 20查找成功，删除成功
删除目标：66 ，计算目标元素存储地址:66%13=1； 66查找失败，删除失败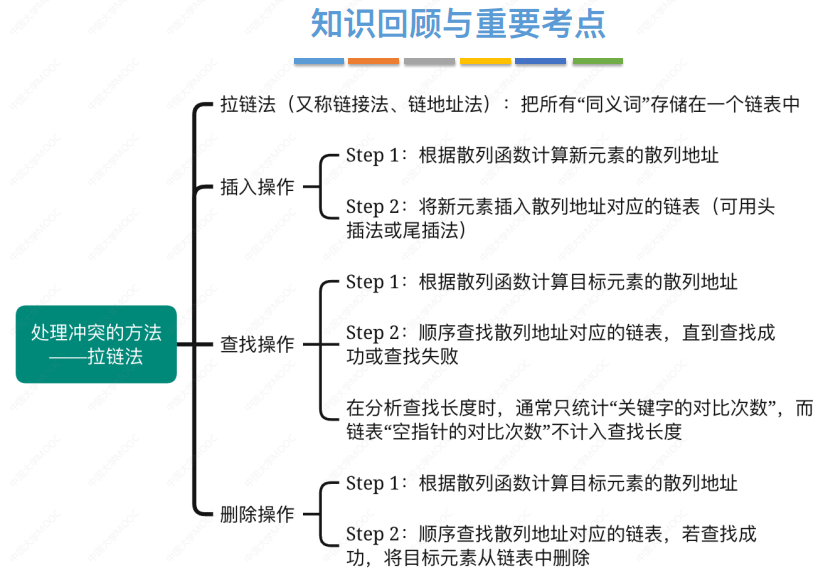

7.5.3_2 处理冲突的方法_开放定址法

开放定址法的基本原理

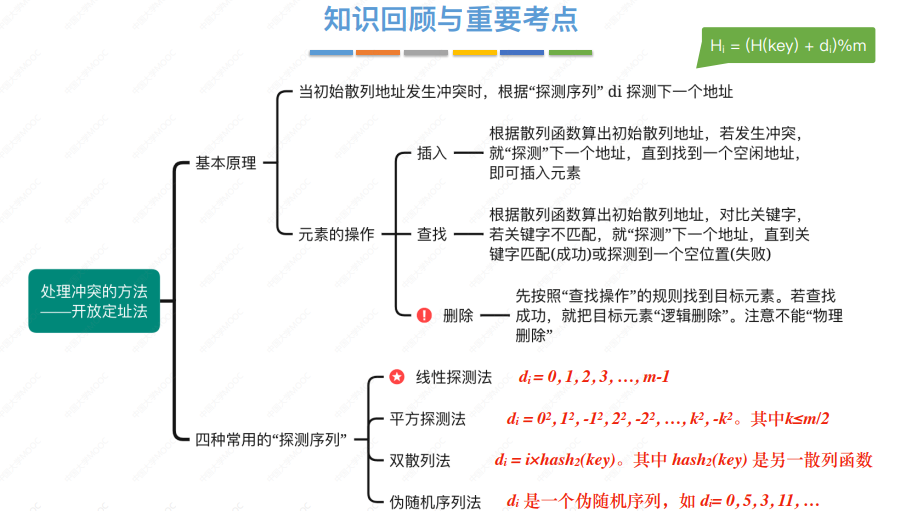
开放定址法︰如果发生“冲突”，就给新元素找另一个空闲位置。

注:d表示第i次发生冲突时，下一个探测地址与初始散列地址的相对偏移量。

根据散列函数H(key)，求得初始散列地址。若发生冲突，如何找到“另一个空闲位置”?

如何删除一个元素:
Step 1∶先根据散列函数算出散列地址，并对比关键字是否匹配。若匹配，则“查找成功”
Step 2∶若关键字不匹配，则根据“探测序列”对比下一个地址的关键字，直到“查找成功”或“查找失败”
Step 3:若“查找成功”，则删除找到的元素

特别注意:关于删除操作
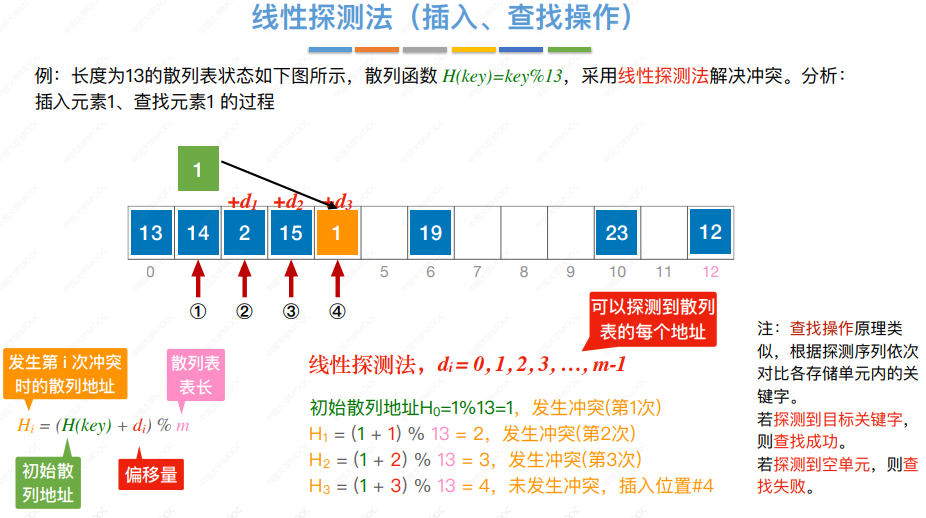
例︰长度为13的散列表状态如下图所示，散列函数H(key)=key%13，采用线性探测法解决冲突。



正确示范:查找元素1
计算元素1的初始散列地址=1%13=1。对比位置#1，关键字不等于1;
根据线性探测法的探测序列，继续对比位置#2，关键字不等于1;
根据线性探测法的探测序列，继续对比位置#3，该位置原关键字已删，继续探测后一个位置;
根据线性探测法的探测序列，继续对比位置#4，关键字等于1，查找成功。