一、引言
1、机器学习分类与预测算法的重要性
在数据驱动的时代,机器学习已经成为了处理和分析大规模数据的关键工具。分类与预测作为机器学习的两大核心任务,广泛应用于各个领域,如金融、医疗、电商等。分类算法能够对数据进行有效归类,帮助我们理解数据的内在结构和规律;而预测算法则能够基于历史数据对未来的趋势进行推断,为决策提供有力支持。
分类算法如支持向量机、决策树、随机森林等,能够自动学习数据的特征,并根据这些特征将数据划分为不同的类别。这种自动化、智能化的分类方式,不仅提高了分类的准确性和效率,还能够处理复杂、高维的数据集。预测算法则能够根据已有的数据,构建出数据之间的关联关系,进而对未来的数据进行预测。例如,在股票价格预测、销售额预测等场景中,预测算法能够帮助我们把握市场趋势,制定更加科学的决策。
2、算法评价的意义与目的
对于机器学习算法而言,仅仅实现算法的功能是不够的,我们还需要对算法的性能进行评价。算法评价的意义在于,它能够帮助我们了解算法的优劣,从而选择出最适合当前任务的算法。同时,通过算法评价,我们还可以发现算法存在的问题和不足,为算法的改进和优化提供方向。
算法评价的目的主要有两个方面:一是比较不同算法的性能,找出在当前任务下表现最佳的算法;二是评估算法的稳定性和泛化能力,确保算法能够在不同的数据集和场景下都能保持较好的性能。通过算法评价,我们可以更加全面、客观地了解算法的性能特点,为实际应用提供有力支持。
二、分类算法评价方式介绍
在机器学习中,分类算法的性能评价是至关重要的一环。不同的评价指标能够从不同角度反映算法的优劣,从而帮助我们更全面地理解算法的性能特点。以下将详细介绍几种常见的分类算法评价方式。
1. 准确率(Accuracy)
准确率是最直观也最常用的分类算法评价指标之一。它定义为正确分类的样本数占总样本数的比例。计算公式如下:
A c c u r a c y = T P + T N T P + F P + F N + T N × 100 % Accuracy =\frac {TP + TN}{TP + FP + FN + TN} \times 100\% Accuracy=TP+FP+FN+TNTP+TN×100%
其中,
- TP表示真正例(True Positive):正确的肯定表示正确肯定的分类数。
- TN表示真反例(True Negative):正确的否定表示正确否定的分类数。
- FP表示假正例(False Positive):错误的肯定表示错误肯定的分类数。
- FN表示假反例(False Negative):错误的否定表示错误否定的分类数。
准确率的优点在于计算简单,易于理解。然而,它也有明显的局限性,特别是在处理不平衡数据集时,准确率可能会产生误导。例如,在二分类问题中,如果正例的数量远少于反例,即使算法将所有样本都预测为反例,准确率也可能很高,但这显然不是一个好的分类器。
适用场景: 准确率适用于类别分布相对均衡的数据集,以及对于误分类代价相差不大的情况。
2. 精确率(Precision)与召回率(Recall)
精确率和召回率是另外两个重要的分类算法评价指标。精确率定义为真正例占所有预测为正例的样本的比例,召回率定义为真正例占所有实际为正例的样本的比例。计算公式如下:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
×
100
%
Precision = \frac {TP} {TP + FP} \times 100\%
Precision=TP+FPTP×100%
R
e
c
a
l
l
=
T
P
T
P
+
F
N
×
100
%
Recall = \frac {TP} {TP + FN} \times 100\%
Recall=TP+FNTP×100%
精确率和召回率常常需要权衡考虑。在某些情况下,我们可能更关注精确率,例如在垃圾邮件检测中,我们希望尽可能减少误判为垃圾邮件的正常邮件(即降低FP);而在其他疾病检测中,我们可能更关注召回率,以确保尽可能少的疾病患者被漏检(即降低FN)。这种权衡关系可以通过绘制P-R曲线来直观展示。
P-R曲线的绘制与解读:P-R曲线是以召回率为横轴,精确率为纵轴绘制的曲线。曲线上的每一个点都对应一个阈值,通过改变这个阈值,我们可以得到不同的精确率和召回率组合。曲线越靠近右上角,说明算法的性能越好。
应用实例解释:以疾病检测为例,假设我们有一个疾病检测算法,通过调整分类阈值,我们可以得到不同的P-R曲线。如果曲线的右上部分较为陡峭,说明算法在保持高精确率的同时也能获得较高的召回率,这是一个性能较好的算法。
3. F1值
F1值是精确率和召回率的调和平均值,用于综合考虑这两个指标。计算公式如下:
F 1 = 2 ∗ P r e c i s i o n ∗ R e c a l l P r e c i s i o n + R e c a l l F1 = 2 * \frac{Precision * Recall}{Precision + Recall} F1=2∗Precision+RecallPrecision∗Recall
F1值越高,说明算法在精确率和召回率上都表现较好。F1值在平衡精确率与召回率中起到了关键作用,尤其是在我们需要同时关注这两个指标的场景下。
4. ROC曲线与AUC值
ROC曲线(Receiver Operating Characteristic Curve)是另一个常用的分类算法评价工具。它以假正例率(FPR)为横轴,真正例率(TPR)为纵轴绘制曲线。计算公式如下:
F
P
R
=
F
P
F
P
+
T
N
FPR = \frac{FP}{FP + TN}
FPR=FP+TNFP
T
P
R
=
T
P
T
P
+
F
N
TPR = \frac{TP}{TP + FN}
TPR=TP+FNTP
AUC值(Area Under the Curve)则是ROC曲线下的面积,用于量化评价分类器的性能。AUC值越接近1,说明分类器的性能越好;AUC值越接近0.5,说明分类器的性能越接近随机猜测。
ROC曲线的绘制与解读:通过不断改变分类器的阈值,我们可以得到一系列的点对(FPR, TPR),将这些点连接起来就形成了ROC曲线。理想的ROC曲线应该尽可能靠近左上角,即TPR尽可能高而FPR尽可能低。
AUC值的计算与意义:AUC值可以通过计算ROC曲线下的面积得到。AUC值的意义在于它提供了一个量化的指标来评价分类器的性能,而且AUC值对类别分布的不平衡性不敏感,因此在处理不平衡数据集时尤其有用。
ROC-AUC在分类算法评价中的优势:ROC-AUC评价方式能够综合考虑分类器在不同阈值下的性能表现,而且不受类别分布不平衡的影响。这使得ROC-AUC成为一个非常稳健和可靠的分类算法评价指标。
5. 混淆矩阵(Confusion Matrix)
混淆矩阵是一个用于展示分类器性能的表格,它能够直观地显示每个类别的分类结果。混淆矩阵的四个基本元素分别是TP、FP、FN和TN,它们分别对应真正例、假正例、假反例和真反例的样本数。
除了基本的四个元素外,基于混淆矩阵我们还可以计算出其他一些有用的指标,如真阳性率(TPR,即召回率)、假阳性率(FPR)、真阴性率(TNR)和假阴性率(FNR)等。这些指标可以从不同角度反映分类器的性能。
混淆矩阵的构成与解读:混淆矩阵的行通常代表实际类别,列代表预测类别。通过查看混淆矩阵,我们可以直接了解到分类器在每个类别上的分类情况,例如,我们可以观察到有多少正例被正确分类(TP),有多少反例被误判为正例(FP)等。
基于混淆矩阵的其他指标:
- 真阳性率(TPR):与召回率相同,表示实际为正例的样本中被正确预测为正例的比例。
- 假阳性率(FPR):表示实际为反例的样本中被错误预测为正例的比例。
- 真阴性率(TNR):表示实际为反例的样本中被正确预测为反例的比例,也称为特异度(Specificity)。
- 假阴性率(FNR):表示实际为正例的样本中被错误预测为反例的比例,也等于1-召回率。
这些指标可以帮助我们更全面地了解分类器的性能,特别是在处理不平衡数据集或关注特定类别性能的场景下。
混淆矩阵在分类问题中的实际应用:在实际应用中,混淆矩阵常常用于对分类器的性能进行详细的诊断和调优。例如,如果发现某个类别的FP很高,可能意味着分类器对这个类别的特征识别不够准确,需要进一步优化特征提取或模型参数。通过不断调整和优化模型,我们可以观察混淆矩阵的变化,从而找到提升分类器性能的关键点。
综上所述,分类算法评价方式多种多样,每种方式都有其特定的适用场景和优缺点。在实际应用中,我们应该根据问题的具体需求和数据特点选择合适的评价方式,以便更准确地评估分类器的性能并进行相应的优化。
三、预测算法评价方式介绍
在机器学习中,预测算法的评价同样至关重要,它帮助我们了解模型预测结果的准确性、稳定性和可靠性。下面将介绍几种常用的预测算法评价方式。
1. 绝对误差与相对误差
设
Y
Y
Y表示实际值,
Y
^
\widehat{Y}
Y
表示预测值,绝对误差
E
E
E是指预测值与实际值之间的差的绝对值,其计算公式为:
E
=
∣
Y
−
Y
^
∣
E = |Y - \widehat{Y}|
E=∣Y−Y
∣
相对误差
e
e
e则是绝对误差与实际值的比值,通常以百分比形式表示,计算公式为:
e
=
Y
^
−
Y
Y
∗
100
%
e = \frac{\widehat{Y} - Y}{Y}* 100\%
e=YY
−Y∗100%
绝对误差和相对误差从不同角度反映了预测的准确性。绝对误差直接给出了预测值与实际值之间的差距,而相对误差则考虑了实际值的大小,使得不同尺度或单位的预测问题可以进行比较。
在预测问题中的应用实例:在股票价格预测中,我们可以计算模型预测的股票价格与实际股票价格之间的绝对误差和相对误差,以评估模型的预测性能。
2. 平均绝对误差(MAE)
平均绝对误差是所有样本绝对误差的平均值,用于衡量预测值与实际值之间的平均偏差。计算公式为:
M
A
E
=
1
n
∑
i
=
1
n
∣
E
i
∣
=
1
n
∑
i
=
1
n
∣
Y
i
−
Y
^
i
∣
MAE = \frac{1}{n} \sum _{i=1}^n|E_i|=\frac{1}{n} \sum _{i=1}^n|Y_i-\widehat{Y}_i|
MAE=n1i=1∑n∣Ei∣=n1i=1∑n∣Yi−Y
i∣
公式中各项的含义如下:
- M A E MAE MAE:平均绝对误差
- E i E_i Ei:第 i i i个实际值与预测值的绝对误差
- Y i Y_i Yi:第 i i i个实际值
-
Y
^
i
\widehat{Y}_i
Y
i:第
i
i
i个预测值
M A E MAE MAE在回归预测中是一个直观且易于理解的指标。它的优点在于对异常值不敏感,因为异常值只会造成误差的线性增加。然而, M A E MAE MAE对于误差的惩罚是恒定的,这可能导致模型在优化过程中过于关注中位数而非平均值。
3. 均方误差(MSE)与均方根误差(RMSE)
均方误差(Mean Squared Error,MSE)是预测值与实际值差值的平方的平均值,计算公式为:
M
S
E
=
1
n
∑
i
=
1
n
(
E
i
)
2
=
1
n
∑
i
=
1
n
(
Y
i
−
Y
^
i
)
2
MSE = \frac{1}{n} \sum _{i=1}^n(E_i)^2=\frac{1}{n} \sum _{i=1}^n(Y_i-\widehat{Y}_i)^2
MSE=n1i=1∑n(Ei)2=n1i=1∑n(Yi−Y
i)2
均方根误差则是均方误差的平方根,计算公式为:
R
M
S
E
=
1
n
∑
i
=
1
n
(
E
i
)
2
=
1
n
∑
i
=
1
n
(
Y
i
−
Y
^
i
)
2
RMSE =\sqrt{\frac{1}{n} \sum _{i=1}^n(E_i)^2}=\sqrt{\frac{1}{n} \sum _{i=1}^n(Y_i-\widehat{Y}_i)^2}
RMSE=n1i=1∑n(Ei)2=n1i=1∑n(Yi−Y
i)2
MSE和RMSE在预测模型性能评估中扮演着重要角色。由于 M S E MSE MSE对误差进行了平方处理,它会对较大的误差给予更大的惩罚,这使得模型在优化过程中更加注重减小大的误差。 R M S E RMSE RMSE则使得误差值与原始数据的单位保持一致,更易于解释。
4. 平均绝对百分误差(MAPE)
平均绝对百分误差是预测误差与实际值百分比的平均值,计算公式为:
M
A
P
E
=
1
n
∑
i
=
1
n
∣
E
i
/
Y
i
∣
=
1
n
∑
i
=
1
n
∣
(
Y
i
−
Y
^
i
)
/
Y
i
∣
MAPE = \frac{1}{n} \sum _{i=1}^n|E_i/Y_i|=\frac{1}{n} \sum _{i=1}^n|(Y_i-\widehat{Y}_i)/Y_i|
MAPE=n1i=1∑n∣Ei/Yi∣=n1i=1∑n∣(Yi−Y
i)/Yi∣
M A P E MAPE MAPE常用于评估预测准确度,尤其当关注预测值与实际值之间的相对差异时。然而,需要注意的是,当实际值为零时, M A P E MAPE MAPE无法计算,因此在实际应用中需要处理这种情况,在工程中一般认为 M A P E MAPE MAPE小于10时,预测精度就比较高。
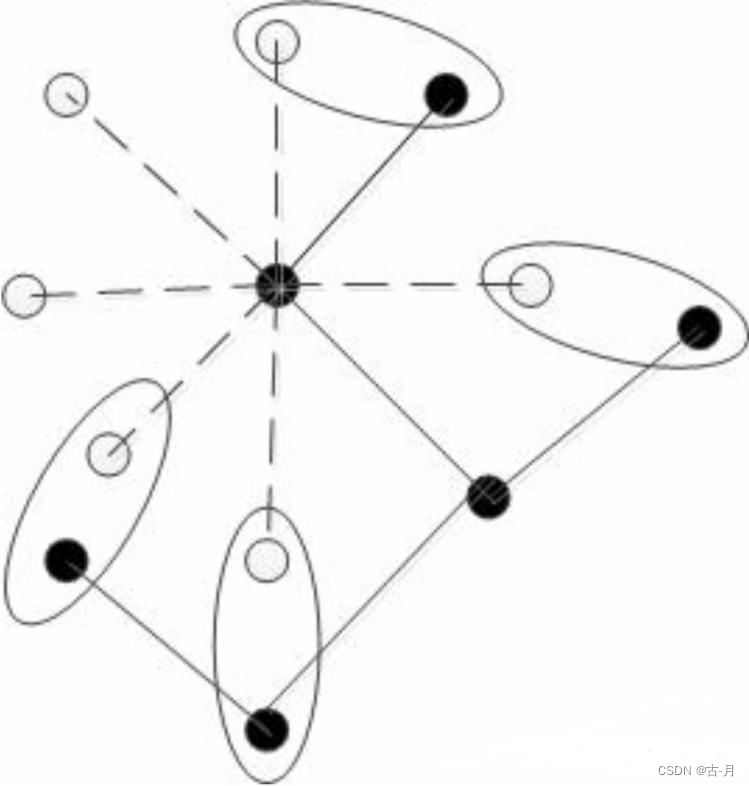
5. Kappa统计
K
a
p
p
a
Kappa
Kappa统计是一种用于分类准确度评估的指标,尤其适用于多分类问题。它通过比较分类器的预测结果与实际结果之间的吻合程度,来评估分类器的性能。Kappa统计值的范围通常在-1到1之间,值越大表示分类器的性能越好,工程中
K
a
p
p
a
Kappa
Kappa系数的取值和真实数据集的关系如下图。

K
a
p
p
a
Kappa
Kappa统计的优势在于它能够考虑到分类问题的随机性,即使分类器的预测结果与实际结果有一定的吻合度,但如果这种吻合度只是由于随机性造成的,那么
K
a
p
p
a
Kappa
Kappa统计值也会很低。然而,
K
a
p
p
a
Kappa
Kappa统计对于类别分布的不均衡性可能较为敏感,因此在处理不平衡数据集时需要谨慎使用,
K
a
p
p
a
Kappa
Kappa系数的计算可以调用sklearn库来实现,具体的调用方式如下:
from sklearn.metrics import cohen_kappa_score
kappa = cohen_kappa_score(np.array(y_true).reshape(-1,1), np.array(y_pred).reshape(-1,1))
Kappa统计的实际应用案例:在图像分类任务中,我们可以使用 K a p p a Kappa Kappa统计来评估分类器对图像标签的预测性能。通过比较预测标签与实际标签的一致性,我们可以得到 K a p p a Kappa Kappa统计值,从而了解分类器在图像分类任务中的表现。
综上所述,不同的预测算法评价方式各有特点,适用于不同的预测问题和场景。在实际应用中,我们需要根据问题的需求和数据的特点选择合适的评价方式,以便更准确地评估预测算法的性能并进行相应的优化。
四、其他评价方式
在机器学习中,除了之前提到的评价方式外,还有一些其他的指标和方法用于分类与预测算法的性能评估。这些评价方式从不同角度提供了对模型性能的深入理解。
1. 对数损失(Log Loss)
对数损失,也称为对数似然损失,常用于评估分类模型的性能,特别是当模型输出的是概率分布时。对数损失的计算基于预测概率与实际标签之间的差异,其公式如下:
L o s s = − ∑ i = 1 n [ y i ∗ l o g ( p i ) + ( 1 − y i ) ∗ l o g ( 1 − p i ) ] Loss = -\sum_{i=1}^n[y_i * log(p_i) + (1 - y_i) * log(1 - p_i)] Loss=−i=1∑n[yi∗log(pi)+(1−yi)∗log(1−pi)]
其中, y i y_i yi是样本 i i i 的实际标签(通常为 0 或 1), p i p_i pi 是模型预测样本 i i i 为正类的概率。对数损失越小,说明模型预测的概率分布与实际标签越接近,模型性能越好。
对数损失在分类问题中的适用性广泛,尤其适用于多分类问题和概率预测。其优势在于能够直接反映模型预测概率的准确性,对于不平衡数据集也具有一定的鲁棒性。
2. 交叉熵(Cross-Entropy)
交叉熵是另一种常用于分类模型评估的指标,它与对数损失密切相关。交叉熵衡量的是两个概率分布之间的差异,其公式与对数损失类似:
L o s s = − ∑ [ y i ∗ l o g ( p i ) ] Loss= -\sum [y_i * log(p_i)] Loss=−∑[yi∗log(pi)]
在二分类问题中,交叉熵与对数损失是等价的。但在多分类问题中,交叉熵需要对每个类别的概率分布进行求和。交叉熵越小,说明模型预测的概率分布与实际标签越接近。
交叉熵在分类模型评估中的应用广泛,尤其是在深度学习领域。通过优化交叉熵损失函数,模型可以学习到更好的特征表示和分类边界。
3. R²决定系数
R 2 R² R2决定系数(也称为确定系数)是回归分析中常用的一个指标,用于评估预测模型对数据的拟合程度。 R 2 R² R2的值介于 0 到 1 之间,越接近 1 表示模型的拟合效果越好。其计算公式如下:
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 / ∑ i = 1 n ( y i − y ˉ ) 2 R² = 1 - \sum_{i=1}^n(y_i - ŷ_i)² / \sum_{i=1}^n(y_i - ȳ)² R2=1−i=1∑n(yi−y^i)2/i=1∑n(yi−yˉ)2
其中, y i y_i yi 是样本 i i i 的实际值, y ^ i ŷ_i y^i 是模型对样本 i i i 的预测值, y ˉ ȳ yˉ 是所有实际值的平均值。分子部分表示模型预测误差的平方和,分母部分表示实际值与平均值之差的平方和。 R 2 R² R2越接近于 1 1 1,说明模型对数据的解释能力越强。
R 2 R² R2在预测模型性能评估中起着重要作用。它不仅可以衡量模型的拟合效果,还可以用于比较不同模型的性能。需要注意的是, R 2 R² R2并不是万能的,它可能受到数据中异常值或噪声的影响,因此在使用时需要结合其他指标进行综合评估。
综上所述,对数损失、交叉熵和R²决定系数是机器学习领域中常用的分类与预测算法评价方式。它们从不同角度提供了对模型性能的深入理解,有助于我们更全面地评估和优化模型。在实际应用中,我们需要根据问题的具体需求和数据特点选择合适的评价方式,以便得到更准确的评估结果。
五、案例分析
在本部分,我们将通过两个具体的案例来展示如何应用前面提到的分类与预测算法评价方式。首先,我们将选取一个图像识别任务进行分类算法的评价;接着,我们将选取一个股票价格预测任务进行预测算法的评价。
1、图像识别任务的分类算法评价
假设我们有一个图像识别的任务,目标是将图像分类为不同的类别。我们将使用深度学习模型(如卷积神经网络CNN)进行训练,并应用上述分类评价方式对模型进行评估。
数据集与预处理过程
我们选择了一个包含多个类别的图像数据集,每个类别都有一定数量的图像样本。在预处理阶段,我们对图像进行了缩放、归一化等操作,以便模型能够更好地学习特征。
应用分类评价方式对模型进行评估
训练好模型后,我们使用测试集对模型进行评估。首先,我们计算了模型的准确率、召回率、F1值等指标。这些指标可以通过混淆矩阵计算得出。然后,我们还计算了模型的Kappa统计值,以进一步评估模型的分类准确度。
下面是使用Python和sklearn库计算这些指标的示例代码:
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.metrics import cohen_kappa_score
import pandas as pd
# 假设 y_true 是真实标签,y_pred 是模型预测标签
y_true = [0,1,0,1,1,1,1,0,0,0,1,0,0,0,0,1,1,0,1,1,1,0] # 真实标签列表
y_pred = [1,1,0,1,1,0,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0] # 模型预测标签列表
# 计算准确率
accuracy = accuracy_score(y_true, y_pred)
print(f"Accuracy: {accuracy:.4f}")
# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)
print("Confusion Matrix:")
print(cm)
# 计算分类报告,包括召回率、精确率和F1值
report = classification_report(y_true, y_pred)
print("Classification Report:")
print(report)
# 计算Kappa统计值
kappa = cohen_kappa_score(np.array(y_true).reshape(-1,1), np.array(y_pred).reshape(-1,1)) # 对于二分类问题
# 对于多分类问题,需要使用其他库或手动计算Kappa值
print(f"Kappa: {kappa:.4f}")
上面的代码输出结果如下:
Accuracy: 0.8182
Confusion Matrix:
[[9 2]
[2 9]]
Classification Report:
precision recall f1-score support
0 0.82 0.82 0.82 11
1 0.82 0.82 0.82 11
accuracy 0.82 22
macro avg 0.82 0.82 0.82 22
weighted avg 0.82 0.82 0.82 22
Kappa: 0.6364
结果分析与讨论
根据计算出的指标值,我们可以对模型的性能进行分析。例如,如果准确率较高且Kappa值接近1,说明模型的分类性能较好。如果某些类别的召回率较低,可能需要针对这些类别进行进一步的优化。
2、股票价格预测任务的预测算法评价
接下来,我们选取一个股票价格预测任务进行预测算法的评价。我们将使用时间序列模型(如LSTM)进行训练,并应用上述预测评价方式对模型进行评估。
数据集介绍与特征工程
我们选择了一个包含历史股票价格数据的数据集,包括开盘价、收盘价、最高价、最低价等特征。在特征工程阶段,我们提取了时间序列的滞后值、移动平均等指标作为模型的输入特征。
应用预测评价方式对模型进行评估
训练好模型后,我们使用测试集对模型进行预测,并计算了平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)等指标来评估模型的预测性能。
下面是使用Python和sklearn库计算这些指标的示例代码:
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import numpy as np
# 假设 y_true 是真实股票价格,y_pred 是模型预测的股票价格
y_true = [31.92,30.87,20.85,25.37,30.00,38.87] # 真实股票价格列表
y_pred = [30.82,31.93,23.75,25.21,29.88,37.77] # 模型预测的股票价格列表
# 计算平均绝对误差(MAE)
mae = mean_absolute_error(y_true, y_pred)
print(f"MAE: {mae:.4f}")
# 计算均方误差(MSE)
mse = mean_squared_error(y_true, y_pred)
print(f"MSE: {mse:.4f}")
# 计算均方根误差(RMSE)
rmse = np.sqrt(mse)
print(f"RMSE: {rmse:.4f}")
# 如果还有实际的目标变量y_true的均值,我们还可以计算R²决定系数
y_true_mean = np.mean(y_true)
total_ss = np.sum((y_true - y_true_mean) ** 2)
res_ss = np.sum((np.array(y_true) - np.array(y_pred)) ** 2)
r2 = 1 - (res_ss / total_ss)
print(f"R²: {r2:.4f}")
上面的代码输出结果如下:
MAE: 1.0733
MSE: 1.9989
RMSE: 1.4138
R²: 0.9360
结果解读与优化建议
股票价格预测任务结果解读
根据计算出的平均绝对误差(MAE)、均方误差(MSE)和均方根误差(RMSE),我们可以对模型的预测性能进行解读。这些指标反映了模型预测值与实际值之间的偏差程度。MAE给出了预测误差的平均绝对值,MSE则给出了预测误差的平方的平均值,而RMSE是MSE的平方根,与原始数据具有相同的量纲,更易于解释。
如果MAE、MSE和RMSE的值较小,说明模型的预测性能较好,能够较准确地预测股票价格。相反,如果这些值较大,说明模型的预测误差较大,可能需要对模型进行进一步的优化。
此外,R²决定系数提供了模型对数据的拟合程度的度量。R²值越接近1,说明模型对数据的解释能力越强,预测性能越好。如果R²值较低,可能意味着模型没有很好地捕捉到数据中的关键信息,需要改进特征选择或模型结构。
优化建议
针对预测性能不佳的情况,我们可以提出以下优化建议:
1. 特征选择与优化:进一步探索与股票价格相关的特征,包括技术指标、基本面数据、市场情绪等,并尝试不同的特征组合和变换方式,以提高模型的预测能力。
2. 模型选择与调参:尝试使用不同的预测模型,如ARIMA、SVR、梯度提升回归等,并对模型参数进行调优,以找到最适合当前数据集的模型配置。
3. 时间序列特性处理:考虑使用更复杂的时间序列处理方法,如季节性调整、趋势分析等,以更好地捕捉股票价格的时间依赖性。
4. 集成学习与堆叠:结合多个模型的预测结果,通过集成学习或堆叠的方式提高整体预测性能。
5. 异常值处理与数据清洗:对原始数据进行异常值检测和处理,以及必要的数据清洗和标准化操作,以减少噪声对模型性能的影响。
通过综合考虑以上优化建议,我们可以对模型进行迭代和改进,以提高股票价格预测的准确性和可靠性。需要注意的是,股票市场受到多种因素的影响,包括宏观经济环境、政策变化、市场情绪等,因此即使经过优化的模型也可能存在一定的预测误差。在实际应用中,我们需要结合其他信息和专业知识进行综合分析和决策。
六、总结与展望
1、分类与预测算法评价方式的总结与比较
在本文中,我们详细探讨了多种分类与预测算法的评价方式。对于分类任务,我们介绍了准确率、精确率、召回率、F1值等常用的评价指标,这些指标能够从多个角度全面评估模型的性能。特别是F1值,它综合考虑了精确率和召回率,为我们提供了一个更加平衡的评估视角。此外,Kappa统计值则进一步考虑了分类的随机性,为我们提供了更加稳健的评估结果。
对于预测任务,我们主要关注了平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)以及R²决定系数等指标。这些指标能够帮助我们衡量预测值与实际值之间的偏差程度,从而评估模型的预测性能。其中,RMSE与原始数据具有相同的量纲,更易于解释;而R²决定系数则能够直观地反映模型对数据的拟合程度。
除了上述常见的评价方式外,我们还介绍了对数损失和交叉熵等适用于特定场景的评价指标。对数损失主要用于评估分类模型的概率预测性能,尤其在多分类问题和不平衡数据集中具有优势;而交叉熵则常用于深度学习领域的分类任务中,通过优化交叉熵损失函数,模型可以学习到更好的特征表示和分类边界。
总体来说,各种评价方式都有其特点和适用场景,我们需要根据具体任务和数据特点选择合适的评价指标。同时,我们也需要注意到,单一的评价指标可能无法全面反映模型的性能,因此在实际应用中,我们通常需要结合多个指标进行综合评估。
2、不同评价方式在实际应用中的选择策略
在实际应用中,选择何种评价方式取决于具体的任务需求和数据特点。对于分类任务,如果关注模型的整体性能,可以选择准确率作为评价指标;如果关注某一类别的识别效果,可以选择精确率或召回率;如果需要综合考虑精确率和召回率,则可以选择F1值。此外,如果数据集存在不平衡现象,Kappa统计值可能是一个更加稳健的选择。
对于预测任务,如果预测目标是连续变量且关注预测值的偏差程度,可以选择MAE、MSE或RMSE等指标;如果关注模型对数据的拟合程度,可以选择R²决定系数。需要注意的是,不同的预测任务可能对数据的噪声和异常值敏感度不同,因此在选择评价方式时需要考虑这一点。
此外,在选择评价方式时,我们还需要考虑计算复杂度和可解释性等因素。一些评价指标计算简单快速,但可能不够准确;而一些复杂的评价指标虽然能够提供更准确的结果,但计算成本可能较高。因此,在实际应用中,我们需要根据具体情况权衡这些因素。
3、机器学习算法评价的未来发展方向
随着机器学习技术的不断发展和应用领域的不断扩展,算法评价也面临着新的挑战和机遇。未来,机器学习算法评价可能会朝着以下几个方向发展:
首先,随着深度学习等复杂模型的普及,我们需要开发更加高效、准确的评价方式,以应对大规模数据和复杂模型的挑战。这可能包括设计新的评价指标、优化评价算法等。
其次,随着多模态数据和跨领域学习的兴起,我们需要探索如何有效地评价这些新型机器学习算法的性能。这可能涉及到融合不同来源的信息、设计跨领域的评价指标等问题。
此外,随着可解释性机器学习的发展,我们也需要关注如何评价模型的解释性。这可能需要开发新的评价指标和方法,以衡量模型在提供解释方面的能力。
最后,随着机器学习在各个领域的应用越来越广泛,我们还需要关注如何将人类的专业知识和经验融入到算法评价中。这可能需要研究如何将专家的判断、意见等纳入到评价过程中,以提高评价的准确性和实用性。
总之,机器学习算法评价是一个持续发展的领域,未来还有许多值得探索和研究的问题。我们相信随着技术的不断进步和应用需求的不断变化,算法评价将会变得更加完善、准确和实用。



![[大模型]MiniCPM-2B-chat WebDemo部署](https://img-blog.csdnimg.cn/direct/0b3600e5dd7e49d1ac1eb1df252b758d.png#pic_center)