这是楼主第一次不靠题解,挑战动态规划的中等题目,虽然最终结果只超过了5%的人,不过我也很满意了。
本题楼主首先采用朴素的递归型动态规划,接着优化算法,使用借助HashMap存储临时数据的递归型动态规划,几次时间复杂度都很高,最后优化成借助数组存储数据的迭代型动态规划。
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 10^4
解题准备:
1.了解可能存在的基础操作:首先,输入只有一个数,应该不会有查找【事实证明,还是有,而且得自己建立数据结构】;;其余看不出来。
2.理解题意:其实用朴素的观点,很容易想到一种解法---对于数据i,先找到i以下的最大平方数(比如10,找到9;或者17,找到16),接着,用i-这个数得到新的i,再用新的i继续此过程,直到i==1,返回一共执行的次数。
不过,这个思路是错误的!
假设i==12,按照此思路,第一步是i-9,得到i=3,接着i==3依次-1,一共执行了4次,返回4;;然而,答案是12=4+4+4,只需要执行3次。
那么,还有其它思路吗?
我们想处理i的完全平方数,需不需要借助i-1、i-2……的完全平方数数据呢?
我们直接处理i,可能有几种情况?
解题难点1分析:
对解题准备的问题进行思考,我们可以发现:
处理i的情况:
1.如果i是完全平方数,比如1,4,9,16,25……那么直接返回1;
2.如果i不是完全平方数,那么可能会有无数种情况(比如刚刚的12=4+4+4),一下子没法处理。
作图如下:
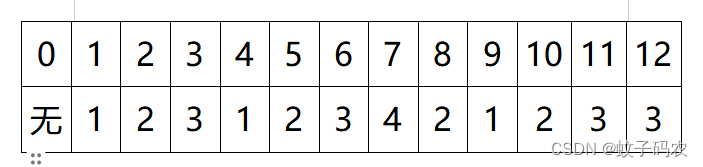
我们可以发现,2的最少完全平方数,就是1+1;
3的最少完全平方数,是1+1+1,形式上等于1+2,并且数目上,1的最少完全平方数和2的最少完全平方数之和,就等于3的最少完全平方数。
不过,对于4不同,对于5好像也不太符合。
继续观察,我们发现,5的最少完全平方数,是4+1,形式上和数目上,都等于1的最少完全平方数+4的最少完全平方数。
其实,如果i不是完全平方数,那么i可以转化为k+n(i=k+n,k、n>=1),如果使k、n最少完全平方数的和最小,就能得到i的最少完全平方数。
比如i是100,那么就从k=1,一直遍历到k=99【当然,为了省时、避免重复,遍历到k=50就差不多】
即i=100, k=1, n=99;
i=100, k=2, n=98;
i=100, k=3, n=97;
……
i=100, k=50, n=50;
这本质上是一种暴力搜索,把所有情况枚举出来,然后选择最少的一个。
原始动态规划递归代码:
我们既然知道了,求i,就得求k+n,又因为k、n>=1,所以k、n必然小于i,那么,只要得到从1到i-1的所有最少完全平方数,就能枚举得到i的最少完全平方数。
求i-1、i-2的最少完全平方数,其结构与求i的类似,所以我们可以使用递归的方法解决。
class Solution {
public int numSquares(int n) {
int res=n;
// 判断是否完全平方数
double temp=Math.sqrt(n);
int l=(int)temp;
if(l-temp==0){
return 1;
}
// 遍历得到从1到i-1的所有最少完全平方数
for(int i=1; i<n/2+1; i++){
res=Math.min(res, numSquares(n-i)+numSquares(i));
}
return res;
}
}这个算法,时间复杂度奇高,由于需要从1到n/2+1,每次调用两个自身(n-i和i),所以可以把递归树看成一个二叉树,该树的深度约为n,且基本上是满二叉树,其时间复杂度可想而知。
我也不确定时间复杂度,不过我猜是O(n/2 * 2^n);
HashMap临时存储动态规划代码:
class Solution {
// 存储临时数据
Map<Integer, Integer> data=new HashMap<>();
public int numSquares(int n) {
int res=n;
// 判断是否为完全平方数
double temp=Math.sqrt(n);
int l=(int)temp;
if(l-temp==0){
return 1;
}
// 同样的递归,实质一样,不过先从临时数据中查看有无
for(int i=1; i<n/2+1; i++){
if(data.get(i)!=null){
if(data.get(n-i)!=null){
res=Math.min(res, data.get(i)+data.get(n-i));
}else{
res=Math.min(res, data.get(i)+numSquares(n-i));
}
}else if(data.get(n-i)!=null){
res=Math.min(res, data.get(n-i)+numSquares(i));
}else{
res=Math.min(res, numSquares(n-i)+numSquares(i));
}
}
data.put(n, res);
return res;
}
}这个算法,节省至少一半的时间,实质上,由于把从1到i-1的数据都保存了,应该能使复杂度到O(n/2 * n!);
解题难点2分析:
不过,即使是竭尽所能,时间上仍然超出限制。
所以,不得不考虑更加复杂的迭代型动态规划。
根据上述思路,我们已经知道如何处理i,那么,怎么处理1到i-1,并存储起来呢?
首先,已知,对于i这个大问题,只要它不是完全平方数,解法就是拆分成两个数,然后求出所有解,拿到最小的一个。
那么,第一步,至少得有两个基本数据,一般选取1、2作为基本数据。
接着,我们需要一个数据结构来存储基本数据,比如HashMap,我采用的是数组,其随机访问的特性非常有用。
声明数组dp,就得知道它多大,从1存储到i-1,所以是i-1这么大。为了保险,选取i作为大小。
此时,满足dp[0]=1, dp[1]=2;
接下来,就是遍历运算。
按理说,对于数据i,i=k+n,所以只需要从k=1,遍历到i/2+1即可得到其最少完全平方数。
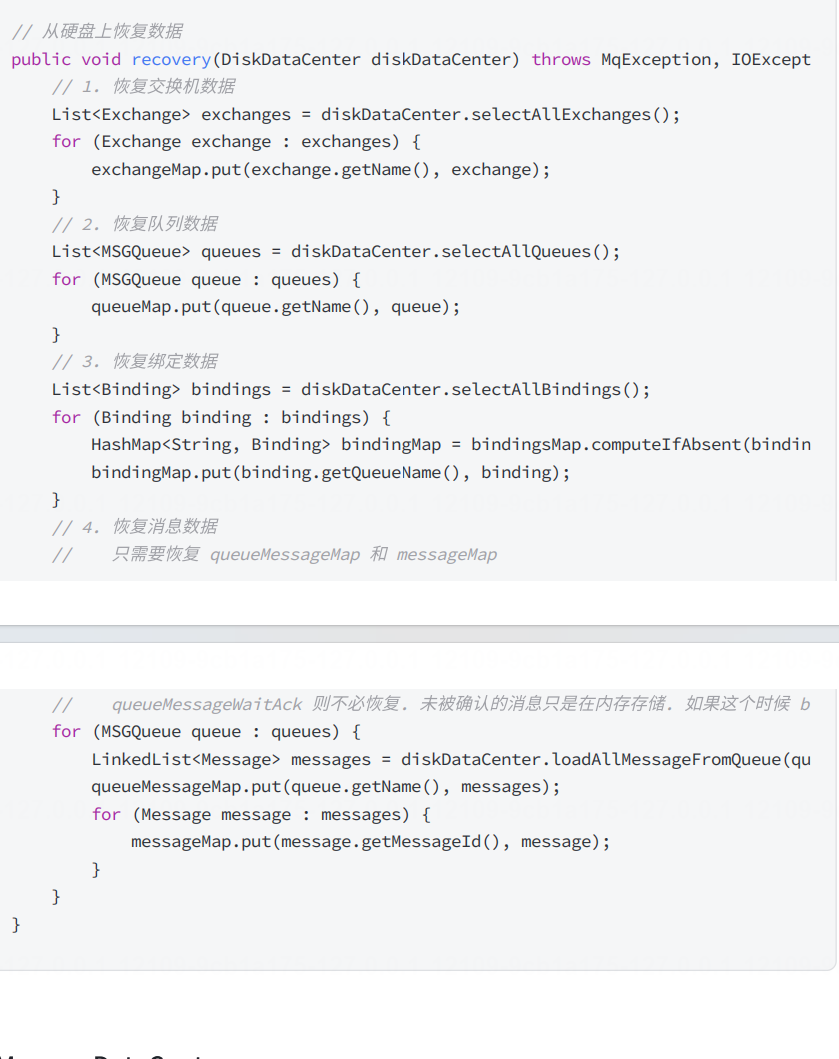
数组存储的动态规划代码:
class Solution {
public int numSquares(int n) {
int[] dp=new int[n]; // 声明数组
int res=n; // 保险起见
// 判断是否为完全平方数
double temp=Math.sqrt(n);
int l=(int)temp;
if(l-temp==0){
return 1;
}
// 从3开始,因为1、2已经得到
int i=3;
dp[0]=1;
dp[1]=2;
// i<n,即遍历到n-1
while(i<n){
// 在遍历时,不可避免地可能存在完全平方数
temp=Math.sqrt(i);
l=(int)temp;
if(l-temp==0){
dp[i-1]=1;
i++;
// 记得continue,否则执行下面的语句后,出错
continue;
}
// 保险
res=i;
// 迭代得到最少完全平方数
for(int k=1; k<i/2+1; k++){
res=Math.min(res, dp[k-1]+dp[i-k-1]);
}
// 记录
dp[i-1]=res;
i++;
}
// 拿到真实结果
res=n;
for(int ln=1; ln<n/2+1; ln++){
res=Math.min(res, dp[ln-1]+dp[n-ln-1]);
}
return res;
}
}题解的思路则非常简洁,我会在接下来的算法补充中说明。
以上内容即我想分享的关于力扣热题17的一些知识。
我是蚊子码农,如有补充,欢迎在评论区留言。个人也是初学者,知识体系可能没有那么完善,希望各位多多指正,谢谢大家。