矩阵乘计算GPU实现中通常为线程块计算一个较大的[m_tile, k] *[k, n_tile]的矩阵乘，最后分配到每个线程后同样为每个线程计算更小的一个[m_tile, k] *[k, n_tile]。

这样存在的一个问题主要是在于m和n较小而k很大时，如下图所示的矩阵乘案例，只能分配很少的线程和线程块，并且每个线程内部的循环次数很大，GPU无法被充分利用，导致矩阵乘实现的性能比较差。这种情况可能广泛出现在卷积通过im2col/im2row方法转换得到的矩阵乘：OpenPPL 中的卷积优化技巧 - 知乎

splitk的原理则是把矩阵乘的k方向split成多个k_n更小的k_size，从而得到了k_n个[m, k_tile] x [k_tile, n]矩阵乘，每个矩阵乘的k loop大小缩短，从而每个线程的计算时间缩短，并且可以创建更多的线程数量来执行计算。

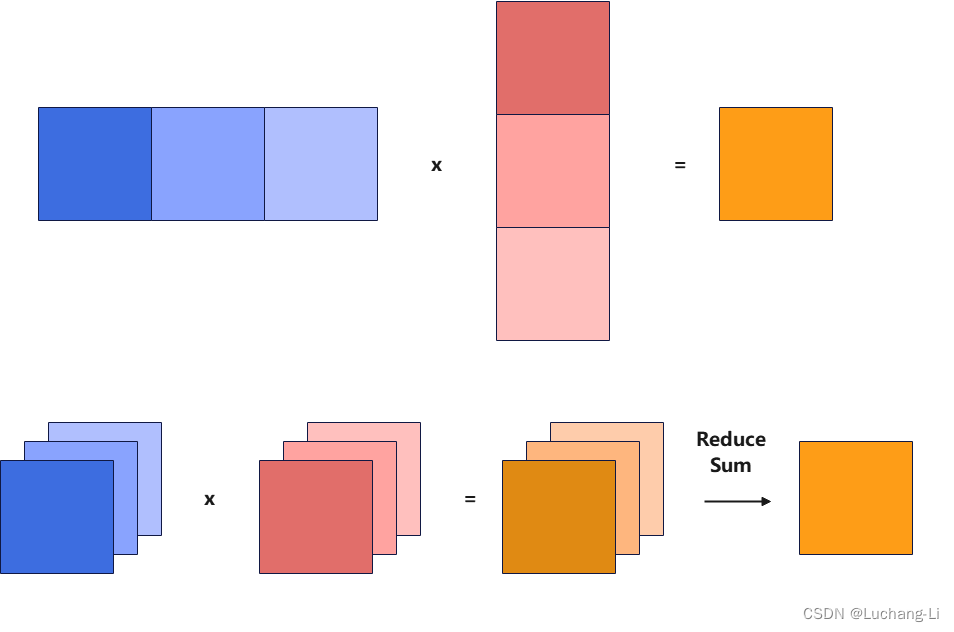
基本原理如下图所示，也就是并行计算多个k更小的矩阵乘，并且增加一个额外的ReduceSum算子进行累加计算。

有没有一个简单的方法来实现上述优化呢？

答案是可以通过一个非常简单通用的图优化，而不需要新增和修改推理引擎现有的算子实现，但是可能性能比专门实现的splitk矩阵乘略差点。

假定矩阵乘input a的shape为[Ba, M, K]。 Ba为input a的batch，可以为任一多个维度。现在首先进行一个reshape得到[Ba, M, Kn, K0]，然后进行一个transpose得到[Ba, Kn, M, K0]，即可得到splitk后矩阵乘新的input a。

同样矩阵乘input b的shape为[Bb, K, N]。Bb为input b的batch，可以为任一多个维度。现在进行reshape得到[Bb, Kn, K0, N]，即为splitk后矩阵乘新的input b。

那么[Ba, Kn, M, K0]与[Bb, Kn, K0, N]的batch矩阵乘就达到了split k的效果。最后在矩阵乘算子后面插入一个ReduceSum(axis=-3)，即可完成。

这个图优化插入了两个reshape，一个transpose，一个reduce。reduce不可避免，reshape算子实际上只是内存重解释，不需要真正计算耗时。因此相比专门的splitk矩阵乘多了一个transpose耗时，当然通常这个算子耗时远远低于矩阵乘的耗时。

在NV GPU这个方法性能收益可能没有端侧GPU那么高，因为端侧GPU很难使用shared mem加速，本文的方法反而可能是一种不错的方法。

numpy参考代码

import numpy as np

shape_a = [1, 49, 2016]
shape_b = [2016, 448]

np.random.seed(1)
data_a = np.random.uniform(-1, 1, size=shape_a).astype("float32")
data_b = np.random.uniform(-1, 1, size=shape_b).astype("float32")

matmul_0 = np.matmul(data_a, data_b)

orig_k = 2016
k_num = 8
k_tile = orig_k // k_num

data_a1 = data_a.reshape([1, 49, k_num, k_tile])
data_a2 = np.transpose(data_a1, [0, 2, 1, 3])
data_b1 = data_b.reshape([k_num, k_tile, 448])

matmul_1 = np.matmul(data_a2, data_b1)

matmul_2 = np.sum(matmul_1, axis=-3)

error = matmul_0 - matmul_2