编程练习：找“单身狗“(三种解题法(不含暴力法))

news2024/11/16 15:41:15

目录

一.问题描述

二. 方法一：排序法

题解代码： 

三.方法二：位运算法

第一步：

第二步：

第三步：

题解代码：

方法三：顺序表记录法

第一步：

第二步：

第三步：

第四步：

题解代码：

一.问题描述

数组arr中只有两个数字是出现一次，其他所有数字都出现了两次。

编写一个函数找出这两个只出现一次的数字。(数组元素个数假设为sz)函数返回一个两个元素的数组的首地址(数组在堆区上创建，该数组中存放数组arr中两个只出现了一次的数字)。

示例：

给定数组{4,2,3,6,7,8,9,10,12,5,2,3,6,7,11,9,10,12,4,5 }; 

函数返回的数组(首地址)：[8,11];

题解接口定义:int* FindNum1(int* arr, int sz);

(函数返回一个存储查找结果的数组)

(sz为数组的大小)

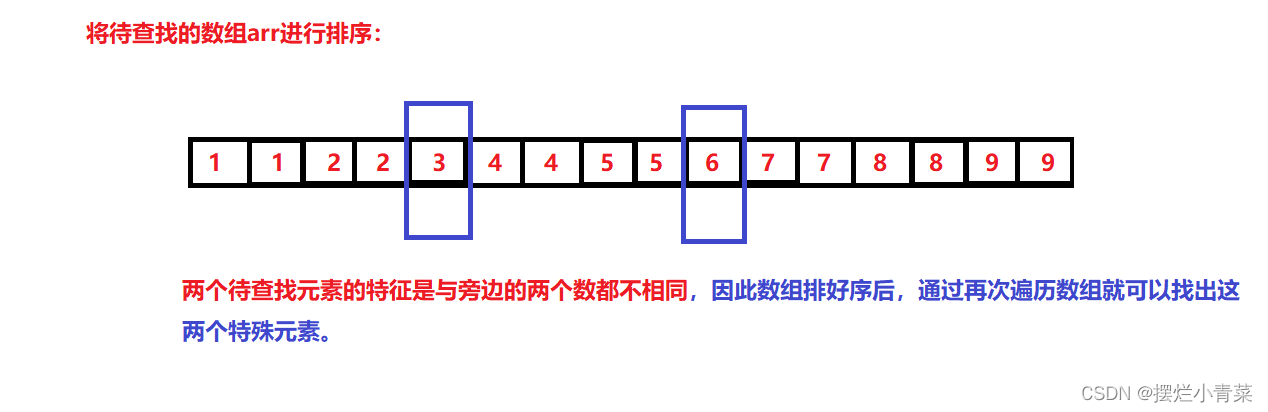
二. 方法一：排序法

注意数组排好序后，当待查找的元素位于数组边界位置时的情况需要单独拎出来判断处理。

 

 

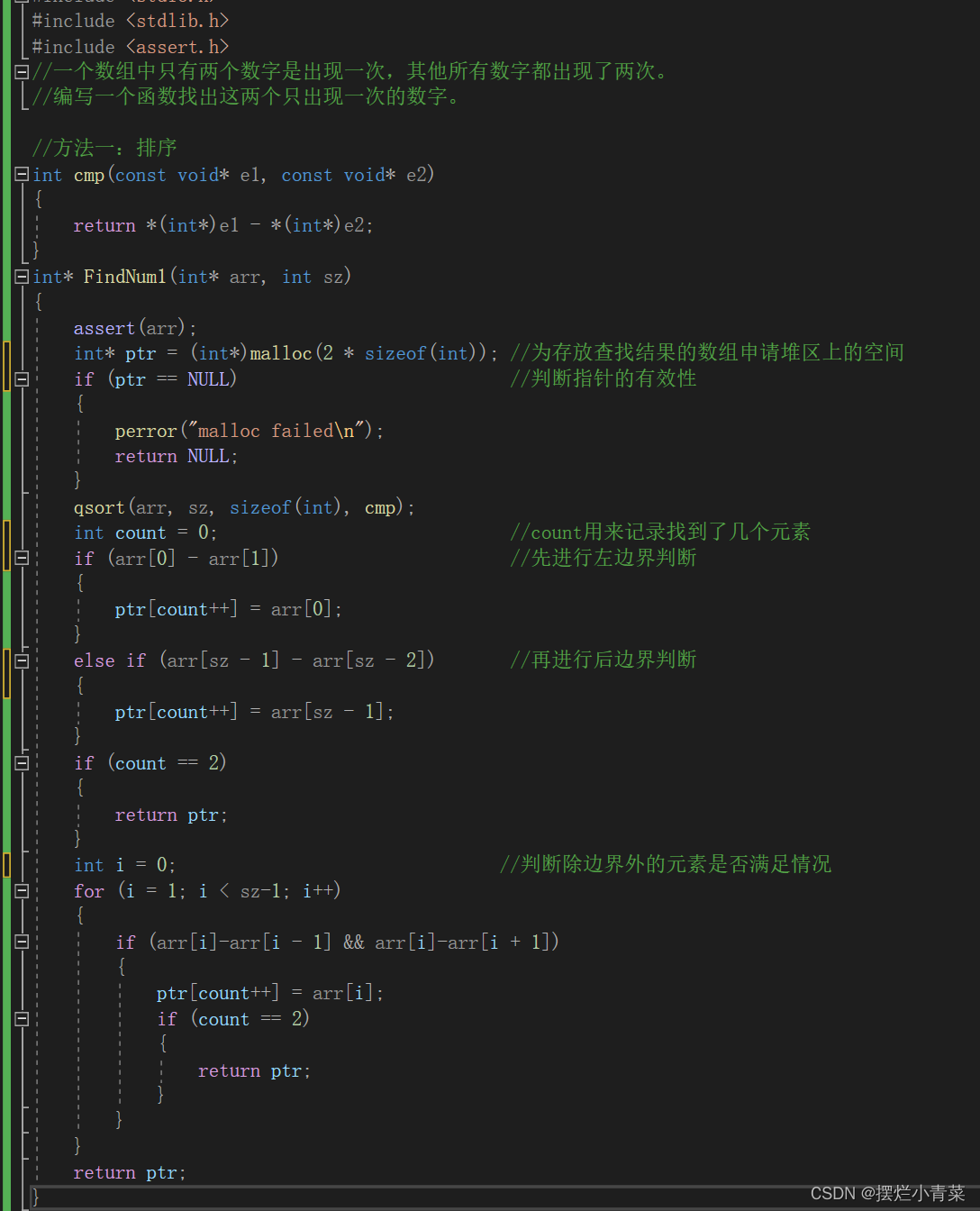
题解代码： 

//方法一：排序
int cmp(const void* e1, const void* e2)
{
	return *(int*)e1 - *(int*)e2;
}
int* FindNum1(int* arr, int sz)
{
	assert(arr);
	int* ptr = (int*)malloc(2 * sizeof(int)); //为存放查找结果的数组申请堆区上的空间
	if (ptr == NULL)                          //判断指针的有效性
	{
		perror("malloc failed\n");
		return NULL;
	} 
	qsort(arr, sz, sizeof(int), cmp);         //用快排对数组进行排序
	int count = 0;                            //count用来记录找到了几个元素     
	if (arr[0] - arr[1])                      //先进行左边界判断
	{
		ptr[count++] = arr[0];
	}
	else if (arr[sz - 1] - arr[sz - 2])       //再进行后边界判断
	{ 
		ptr[count++] = arr[sz - 1];
	}
	if (count == 2)
	{
		return ptr;
	}
	int i = 0;                                //判断除边界外的元素是否满足情况
	for (i = 1; i < sz-1; i++)
	{
		if (arr[i]-arr[i - 1] && arr[i]-arr[i + 1])
		{
			ptr[count++] = arr[i];
			if (count == 2)
			{
				return ptr;
			}
		}
	}
	return ptr;
}

该方法的时间复杂度就是排序的时间复杂度：O(nlogn).

三.方法二：位运算法

数组元素的异或和：将数组所有元素进行异或运算得到的结果.

比如一个数组:[1,2,3,4],则该数组的异或和为：1^2^3^4.

注意异或运算满足交换律和结合律

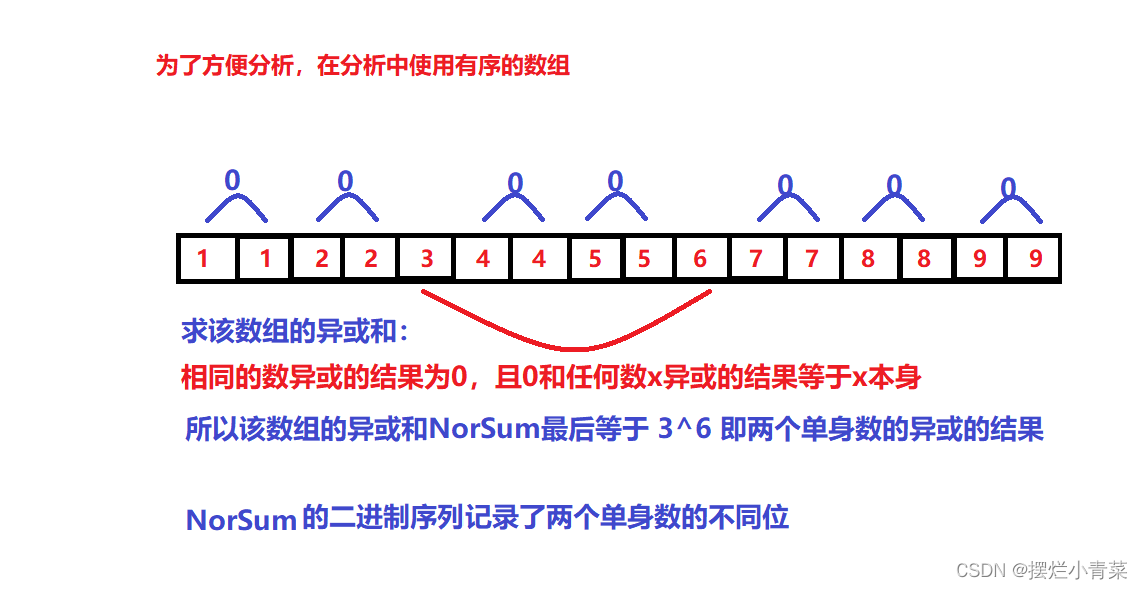
第一步：

求数组arr的异或和NorSum：

	int i = 0;
	int NorSum = 0;                         //0异或x(x为任意值)结果为x，NorSum一定要初始化为0
	for (i = 0; i < sz; i++)
	{
		NorSum ^= arr[i];                   //NorSum=x^y ,NorSum记录了x和y的不同位
	}

第二步：

记录NorSum的某一位1,把该为1记录于lowbit中，用于将数组的元素进行分组

该步骤有两种方法：

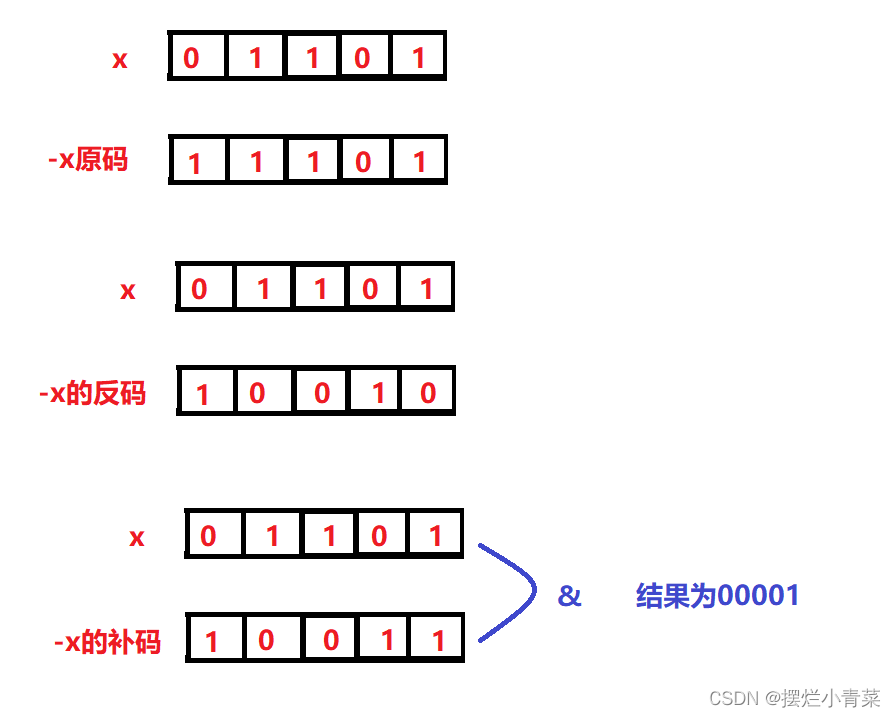
方法1：lowbit= NorSum&(-NorSum)

方法原理：假设x为正数，将x符号位变为1，其余位按位取反，这时得到-x的反码，-x的反码与x的每一位都不一样，这时-x的反码再加上1(这时会得到-x的补码)，其最低位的0就会变为1，而-x的反码的最低位的0对应x最低位的1，所以 -x&x的结果就记录了x的最低位的1。

方法2：利用循环逐位去找NorSum的某一位1并记录其位置：


 for (i = 0; i < 32; i++)
 {
   if (NorSum & (1 << i))
   {
     lowbit= (1<<i);
     break;
   }
 }

lowbit记录了NorSum最低位的1的位置。

我们采用方法1

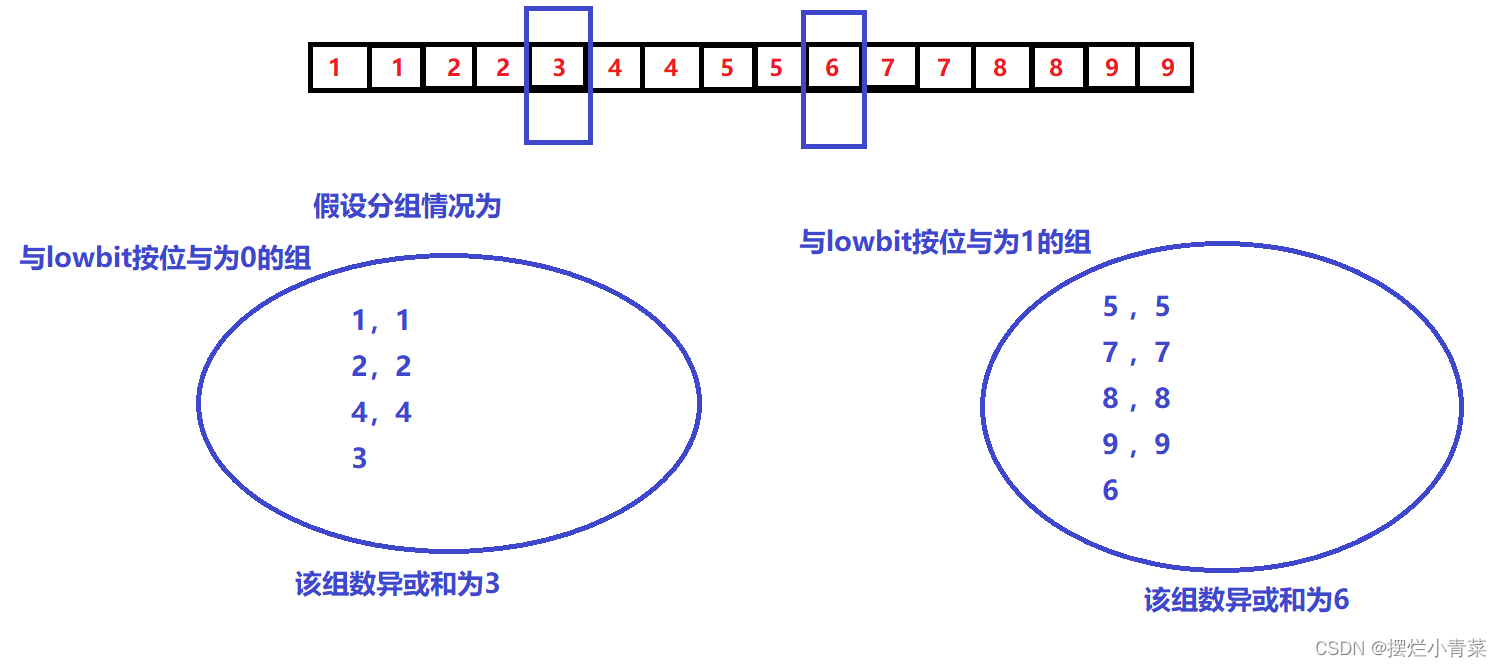
第三步：

利用lowbit以按位与的方式对数组元素进行分组

	int Lowbit = NorSum &(-NorSum);          /*取出NorSum中的最低位，该最低位可以将arr中的数 
                                             分为两组*/                              
	                                         //NorSum位数太多无法用于分组(位数多无法确定分组的 
                                             //可能性)
	int x = 0;
	int y = 0;                               //假设两个单独存在的数分别为x和y
	for (i = 0; i < sz; i++)                 //利用和lowbit按位与的方式将数组元素分为两组
	{                                        //所有成对的数必定出现在同一组，x和y分别会位于不 
                                             //同组
		if ((Lowbit & (arr[i])) == 0)        //分别求两组数的异或和就可以得到x和y
		{ 
			x ^= arr[i];
		}
		else
		{
			y ^= arr[i];
		}
	}

题解代码：

 

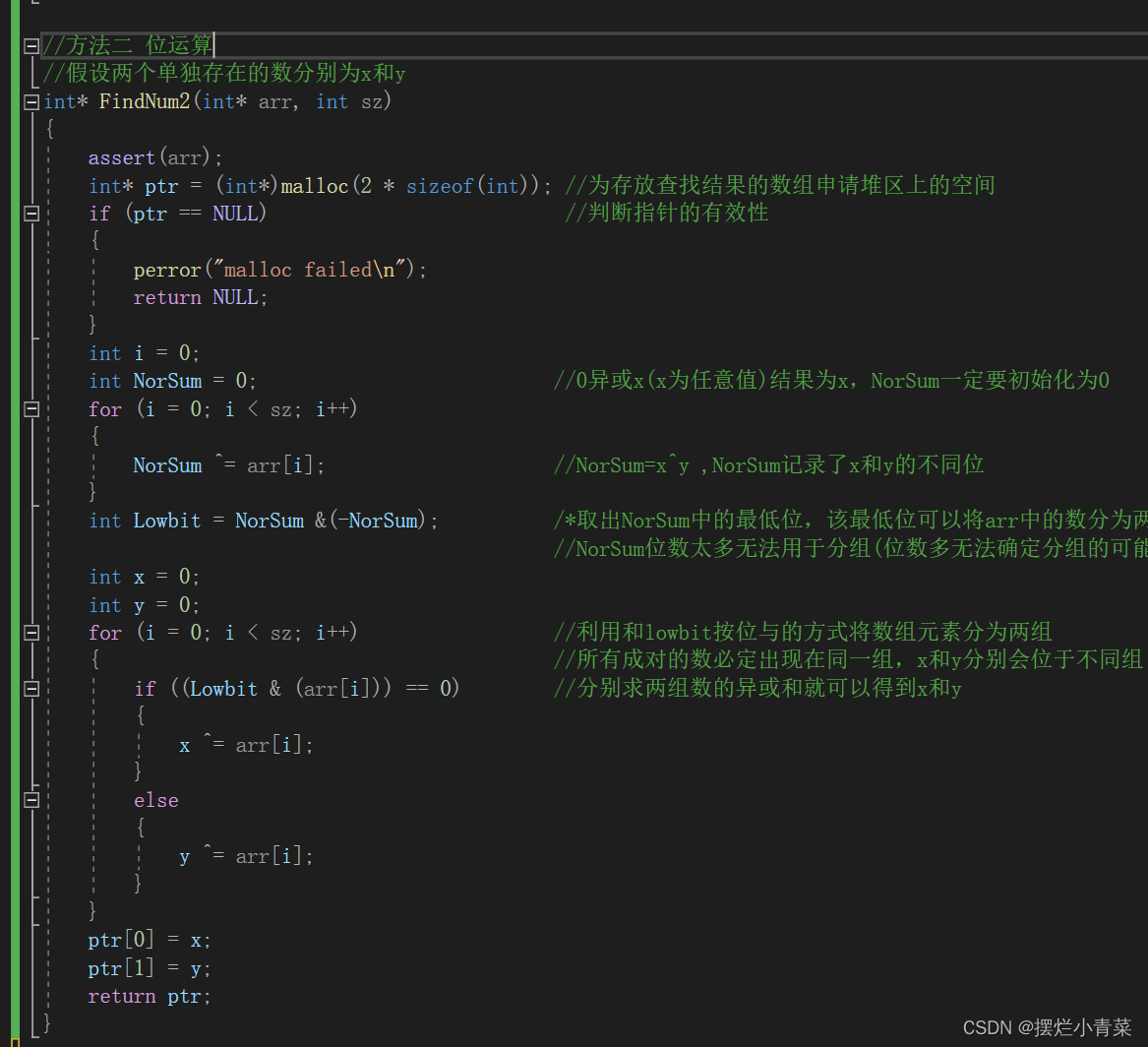
//方法二 位运算
//假设两个单独存在的数分别为x和y
int* FindNum2(int* arr, int sz)
{
	assert(arr);
	int* ptr = (int*)malloc(2 * sizeof(int)); //为存放查找结果的数组申请堆区上的空间
	if (ptr == NULL)                          //判断指针的有效性
	{
		perror("malloc failed\n");
		return NULL;
	}
	int i = 0;
	int NorSum = 0;                          //0异或x(x为任意值)结果为x，NorSum一定要初始化 
                                             //为0
	for (i = 0; i < sz; i++)
	{
		NorSum ^= arr[i];                    //NorSum=x^y ,NorSum记录了x和y的不同位
	}
	int Lowbit = NorSum &(-NorSum);          /*取出NorSum中的最低位，该最低位可以将arr中的 
                                             //数分为两组*/                              
	                                         //NorSum位数太多无法用于分组(位数多无法确定分 
                                             //组的可能性)
	int x = 0;
	int y = 0;
	for (i = 0; i < sz; i++)                 //利用和lowbit按位与的方式将数组元素分为两组
 	{                                        //所有成对的数必定出现在同一组，x和y分别会位于 
                                             //不同组
		if ((Lowbit & (arr[i])) == 0)        //分别求两组数的异或和就可以得到x和y
		{ 
			x ^= arr[i];
		}
		else
		{
			y ^= arr[i];
		}
	}
	ptr[0] = x;
	ptr[1] = y;
	return ptr;
}

该方法的时间复杂度是线性的:O(n)

方法三：顺序表记录法

 

第一步：

找到数组中的最大值和最小值：

	int max = arr[0];
	for (i = 1; i < sz; i++)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	int min = arr[0];
	for (i = 1; i < sz; i++)
	{
		if (arr[i] < min)
		{
			min = arr[i];
		}
	}

第二步：

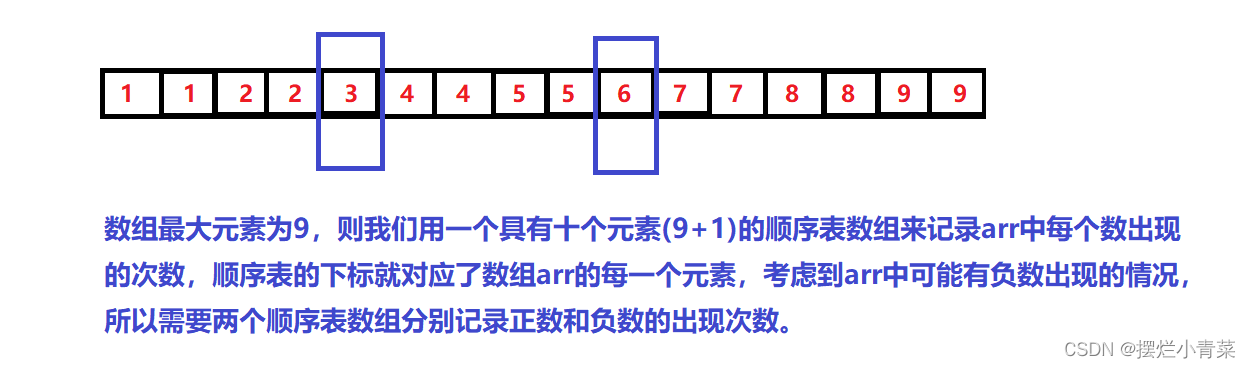
用最大值和最小值去创建顺序表tablePos和tableNeg分别用于记录数组中正数和负数的出现次数

	int* tablePos = (int*)calloc(max+1,sizeof(int));
	if (NULL==tablePos)
	{
		perror("malloc failed\n");
		return NULL;
	}
	int* tableNeg = (int*)calloc(Abs(min) + 1, sizeof(int));
	if (NULL==tableNeg)
	{
		perror("malloc failed\n");
		return NULL;
	}

第三步：

遍历数组将各元素出现次数记录在表中

	for (i = 0; i < sz; i++)
	{
		if (arr[i] >= 0)
		{
			tablePos[arr[i]]++;
		}
		else
		{
			tableNeg[Abs(arr[i])]++;
		}
	}

第四步：

遍历顺序表找到值为1的元素。

	ptr是记录单身数的数组
    int count = 0;                     count记录找到的单身数的个数
	for (i = 0; i < (max + 1); i++)
	{
		if (1 == *(tablePos+i))
		{
			ptr[count++] = i;
			if (2 == count)
			{
				free(tablePos);
				free(tableNeg);
				return ptr;
			}
		}
	}
	for (i = 0; i < Abs(min); i++)      Abs是求绝对值的函数
	{
		if (1==tableNeg[i])
		{
			ptr[count++] = -i;
			if (2==count)
			{
				free(tablePos);
				free(tableNeg);
				return ptr;
			}
		}
	}

题解代码：

//方法三：顺序表记录法
int Abs(int num)                              //封装一个求绝对值的函数
{
	return num >= 0 ? num : -num;
}
int* FindNum3(int* arr, int sz)
{
	assert(arr);
	int* ptr = (int*)malloc(2 * sizeof(int)); //为存放查找结果的数组申请堆区上的空间
	if (NULL==ptr)                            //判断指针的有效性
	{
		perror("malloc failed\n");
		return NULL;
	}

	int i = 0;

	int max = arr[0];
	for (i = 1; i < sz; i++)
	{
		if (arr[i] > max)
		{
			max = arr[i];
		}
	}
	int min = arr[0];
	for (i = 1; i < sz; i++)
	{
		if (arr[i] < min)
		{
			min = arr[i];
		}
	}



	int* tablePos = (int*)calloc(max+1,sizeof(int));
	if (NULL==tablePos)
	{
		perror("malloc failed\n");
		return NULL;
	}
	int* tableNeg = (int*)calloc(Abs(min) + 1, sizeof(int));
	if (NULL==tableNeg)
	{
		perror("malloc failed\n");
		return NULL;
	}



	for (i = 0; i < sz; i++)
	{
		if (arr[i] >= 0)
		{
			tablePos[arr[i]]++;
		}
		else
		{
			tableNeg[Abs(arr[i])]++;
		}
	}



	int count = 0;
	for (i = 0; i < (max + 1); i++)
	{
		if (1 == *(tablePos+i))
		{
			ptr[count++] = i;
			if (2 == count)
			{
				free(tablePos);
				free(tableNeg);
				return ptr;
			}
		}
	}
	for (i = 0; i < Abs(min); i++)
	{
		if (1==tableNeg[i])
		{
			ptr[count++] = -i;
			if (2==count)
			{
				free(tablePos);
				free(tableNeg);
				return ptr;
			}
		}
	}
	free(tablePos);
	free(tableNeg);
	return ptr;
}

该方法的时间复杂度也是线性的：O(n)

 相似的题目leetcode链接：645. 错误的集合 - 力扣（Leetcode）

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/160702.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

c语言tips-【C语言多线程编程】

c语言tips-【C语言多线程编程】

0.摘要 操作系统具有管理进程&#xff0c;进程调度的能力&#xff0c;线程&#xff0c;决定哪个进程、线程使用 CPU。很多时候我们需要在同一时间干不同的任务&#xff0c;这就需要我们通过多进程或者多线程来进行&#xff0c;在我们学习和工作中我们大部分用到的都是多线程,本…
阅读更多...
SAP FICO 成本估算解析

SAP FICO 成本估算解析

成本估算解析 物料成本构成组件分类&#xff0c;比如下图中的G&#xff08;Overhead&#xff09;、L&#xff08;Subcontracting&#xff09;、E&#xff08;Internal Activity&#xff09;等。 同时它也分不同的视图&#xff0c;每个视图中包含了不同的组件。 对同一个工厂的同…
阅读更多...
SpringEvent的使用

SpringEvent的使用

步骤&#xff1a;定义事件&#xff0c;继承ApplicationEvent定义监听&#xff0c;要么实现ApplicationListener接口&#xff0c;要么在方法上添加EventListener注解发布事件&#xff0c;调用ApplicationContext.publishEvent()或者ApplicationEventPublisher.publishEvent();1、…
阅读更多...
附录C：Standard Parasitic Extraction Format(SPEF)

附录C：Standard Parasitic Extraction Format(SPEF)

文章目录C.1 基础(Basics)C.2 格式(Format)C.3 完整语法知乎翻译圣经本附录将介绍标准寄生参数提取格式&#xff08;SPEFSPEFSPEF&#xff09;&#xff0c;它是IEEEStd1481IEEE\ Std\ 1481IEEE Std 1481标准的一部分。 C.1 基础(Basics) SPEFSPEFSPEF允许以ASCIIASCIIASCII交换…
阅读更多...
代码整洁之道，好的代码就是为了更美好的生活。

代码整洁之道，好的代码就是为了更美好的生活。

美国童子军有一条简单的军规&#xff1a;让营地比你来时更干净。当梳理代码时&#xff0c;坚守此军规&#xff1a;每次 review 代码&#xff0c;让代码比你发现它时更整洁。 一位大神说过&#xff1a;“衡量代码质量的唯一有效标准&#xff1a;WTF/min”&#xff0c;并配了一个…
阅读更多...
Manjaro通过源码编译jdk11

Manjaro通过源码编译jdk11

我在编译中遇到的最大的问题就是gcc版本问题&#xff0c;因manjaro是滚动更新&#xff0c;所以gcc也是很新的版本&#xff0c;导致无法编译jdk11 1 下载源码 网上根据关键词查找jdk源码&#xff0c;查找出来很多可以下载源码的链接&#xff0c;这里我们使用github去官方仓库&a…
阅读更多...
yolov5-6.0网络添加小目标检测头 TensorRT部署

yolov5-6.0网络添加小目标检测头 TensorRT部署

小目标检测使用TPH-YOLOv5 中的yolov5l-xs-tph.yaml模型&#xff1b;对其中的C3STR替换为C3模块&#xff1b;本文的TensorRT部署是基于yolov5l-xs-tph修改后的模型训练部署&#xff0c;其精度一般主要学习如何TensorRT部署&#xff0c;都是在wang-xinyu基础上简单修改&#xff…
阅读更多...
中科大2008年复试机试题

中科大2008年复试机试题

中科大2008年复试机试题 文章目录中科大2008年复试机试题第一题问题描述解题思路及代码第二题问题描述解题思路及代码第三题问题描述解题思路及代码第四题问题描述解题思路及代码第一题 问题描述 一个十进制正整数转换成二进制有多少个1 示例1 输入:10 输出:2解题思路及代码…
阅读更多...
数据分析之Excel

数据分析之Excel

自定义格式 一、自定义格式的结构 方式一: 代码结构组成代码码分为四个部分&#xff0c;中间用”;”号分隔&#xff0c;具体如下: 正数格式;负数格式;零格式;文本格式 两个代码部分&#xff0c;则第一部分用于正数和零, 第二部分用于负数 一个代码部分&#xff0c;则该部分将用…
阅读更多...
【跟彤砸学编程】——第二课（上）

【跟彤砸学编程】——第二课（上）

嗨害嗨大家好&#xff0c;这里是彤砸&#xff01; 今天我们来看看——编程到底是个啥&#xff1f; 上节课滴链接~【跟彤砸学编程】——第一课 程序是什么&#xff1f; 程序数据算法&#xff1b; 数据 生活中到处都是数据—— 1,2,3,是数据 A,B,C是数据 图片是由像素构成&…
阅读更多...
【CSDN年度总结】一个四线城市的程序员-苟延残喘

【CSDN年度总结】一个四线城市的程序员-苟延残喘

个人简介 首先本人从事软件开发工作近8年&#xff0c;在北京工作5年&#xff0c;2020年1月13号回来老家工作&#xff0c;已经整整3年了&#xff01;&#xff01;&#xff01; 现在做工业大数据方面工作&#xff0c;曾就职于华为做手机系统研发工作。 在一个四线城市坚守做一个…
阅读更多...
速看｜低代码平台公司流辰信息为实现企业高效办公积极赋能！

速看｜低代码平台公司流辰信息为实现企业高效办公积极赋能！

流辰信息&#xff0c;历经多年的砥砺奋斗&#xff0c;终于在低代码开发行业斩获越来越多的市场份额&#xff0c;是一家专注于研发低代码产品的低代码平台公司。在持续奋斗的年月中&#xff0c;流辰信息将持续增强研发创新能力&#xff0c;为各企业实现高效办公协作效率强劲赋能…
阅读更多...
XC-15媒资管理系统集成

XC-15媒资管理系统集成

学习页面查询课程计划 需求分析 到目前位置,我们已经可以编辑课程计划信息并且上传课程视频,下一步我们要是心啊在线学习页面动态获取章节对应的视频并且进行播放,在线学习页面所需要的信息有两类,一类是课程计划信息,一类是课程学习信息(视频地址,学习进度等),如下图 在线学…
阅读更多...
我与CSDN相识的一年

我与CSDN相识的一年

一、保持初心&#xff0c;笃定前行&#xff0c;回首2022 1、1 保持初心 回想起与CSDN的相识也是有一年多了。最初的相识也是我刚进入大学的时候。那个时候我还是懵懂无知的一个计算机类的大学生。在老师留下的一次任务中&#xff0c;我发现自己有点解决不了&#xff0c;想上网…
阅读更多...
如何处理mybatis处理数据库关系中的多对一关系呢？

如何处理mybatis处理数据库关系中的多对一关系呢？

测试环境的搭建&#xff1a; 导入lombok&#xff1a; 不懂得小伙伴可移步这篇文章 新建实体类&#xff1a; 拿我们日常生活中最常见的举例&#xff1a;多个学生对应一个老师 对于学生这边而言&#xff0c;关联… 多个学生关联一个老师[多对一] 对于老师而言&#xff0c;集…
阅读更多...
BGP（边界网关路由协议）小实验

BGP（边界网关路由协议）小实验

目录实验要求ospf协议启动关于BGP基本知识点BGP关系建立的配置BGP的宣告实验要求 如下实验拓扑&#xff0c;各个自治系统区域和网段已经标注 基本的ip配置&#xff0c;环回配置就不再展示。 要求&#xff1a;除了R5的环回外&#xff0c;其他环回均可以互相访问 ospf协议启动…
阅读更多...
C语言进阶——自定义类型——位段、枚举、联合

C语言进阶——自定义类型——位段、枚举、联合

结构体 目录 一. 位段 1.概念 2.位段的内存分配 3.位段的跨平台问题 4.位段的应用 二. 枚举 1.枚举类型的定义 2.枚举的优点 3.枚举的使用 三. 联合&#xff08;共用体&#xff09; 1.联合类型的定义 ​编辑 2.联合的特点 3. 联合大小的计算 一. 位段 1.…
阅读更多...
Git 合并多条commit

Git 合并多条commit

文章目录修改前开始修改第一种方式: 命令行第二种方式: Android Studio遇到冲突的解决办法第一种&#xff1a;修改到底,干就完事了第二种&#xff1a;回滚吧&#xff0c;有点慌修改前 开始修改 第一种方式: 命令行 git rebase -i 01fc32484fb2d2229aa20 // 这里对应的是init的…
阅读更多...
osg fbo(四），将颜色缓冲区图片中的牛通过shader变绿

osg fbo(四），将颜色缓冲区图片中的牛通过shader变绿

osg fbo&#xff08;三&#xff09;中&#xff0c;把整个屏幕变绿了&#xff0c;因为是把shader添加到了颜色缓冲区图片上了。如果只想把牛变绿&#xff0c;就需要把shader添加到原始场景根中。 即 osg::ref_ptr<osg::StateSet> statset_SceneRoot sceneRoot->getOr…
阅读更多...
一、Java框架之Spring配置文件开发

一、Java框架之Spring配置文件开发

文章目录1. 基础概念1.1 Spring Framework1.2 核心概念产生背景IoC、Bean、DI2. 入门案例2.1 普通Maven项目2.2 IoC入门案例2.3 DI入门案例3. bean配置3.1 bean基础配置bean的基础配置bean的别名配置bean的作用范围3.2 bean实例化实例化方法1&#xff1a;构造方法实例化方法2&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023