【位运算拆位法二分】3007. 价值和小于等于 K 的最大数字

news2024/9/23 19:14:21

本文涉及知识点

位运算拆位法
二分查找算法合集

LeetCode3007. 价值和小于等于 K 的最大数字

给你一个整数 k 和一个整数 x 。整数 num 的价值是由它的二进制表示中，从最低有效位开始，x，2x，3x，以此类推，这些位置上设置位的数目来计算。下面的表格包含了如何计算价值的例子。
x num Binary Representation Price
1 13 000001101 3
2 13 000001101 1
2 233 011101001 3
3 13 000001101 1
3 362 101101010 2

num 的累加价值是从 1 到 num 的数字的总价值。如果 num 的累加价值小于或等于 k 则被认为是廉价的。
请你返回最大的廉价数字。

示例 1：

输入：k = 9, x = 1
输出：6
解释：由下表所示，6 是最大的廉价数字。
x num Binary Representation Price Accumulated Price
1 1 001 1 1
1 2 010 1 2
1 3 011 2 4
1 4 100 1 5
1 5 101 2 7
1 6 110 2 9
1 7 111 3 12
示例 2：

输入：k = 7, x = 2
输出：9
解释：由下表所示，9 是最大的廉价数字。
x num Binary Representation Price Accumulated Price
2 1 0001 0 0
2 2 0010 1 1
2 3 0011 1 2
2 4 0100 0 2
2 5 0101 0 2
2 6 0110 1 3
2 7 0111 1 4
2 8 1000 1 5
2 9 1001 1 6
2 10 1010 2 8

提示：

1 <= k <= 10¹⁵
1 <= x <= 8

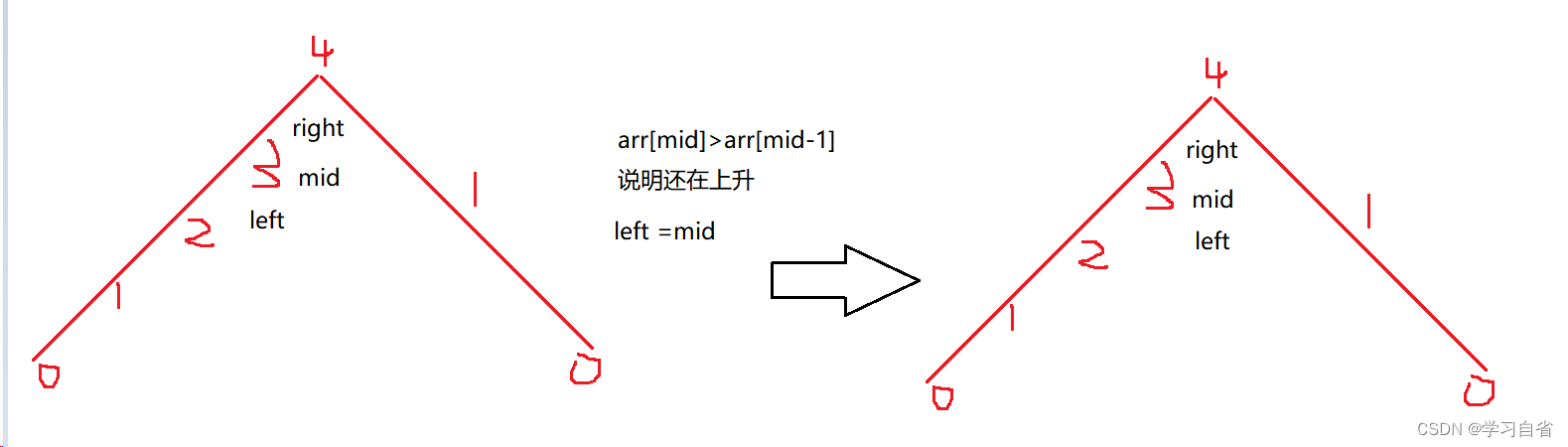
二分

由于价值是自然数，所有随着mid增加而增加或不变，这就有了单调性。
count函数返回mid的积分和,count(mid) <= k符合条件，有多个取最后一个。故用左闭右开空间。
count函数：
枚举x-1,2x-1 $\cdots$ 各为1的数量，long long 出度符合位，63 位，我们权枚举。可以少枚举几位，性能稍微提升。
<= mid的数中有多少个数第y为1:

0到mid共mid+1个数：
第0位： 010101 交替
第1为：00110011 交替
第2位：00001111
一个周期的数量：const long long iUnit = 1LL << (i+1); i为62是会越界，可以用半周期。
z个完整的周期数有一半的数字是1，余下不完整的周期 z1 = (mid+1)%iUnit - iUnit /2
z1 = max(0,z1)
二分的上界为什么是： k*2+10000
x最大是8，故一个完整周期最大是2⁸，远远小于10000。
2k个数加上10000后，至少有2k个数在完整周期内，也就是至少k个数符合要求。

代码

namespace NBinarySearch
{
	template<class INDEX_TYPE, class _Pr>
	INDEX_TYPE FindFrist(INDEX_TYPE left, INDEX_TYPE rightInclue, _Pr pr)
	{
		while (rightInclue - left > 1)
		{
			const auto mid = left + (rightInclue - left) / 2;
			if (pr(mid))
			{
				rightInclue = mid;
			}
			else
			{
				left = mid;
			}
		}
		return rightInclue;
	}

	template<class INDEX_TYPE, class _Pr>
	INDEX_TYPE FindEnd(INDEX_TYPE leftInclude, INDEX_TYPE right, _Pr pr)
	{
		while (right - leftInclude > 1)
		{
			const auto mid = leftInclude + (right - leftInclude) / 2;
			if (pr(mid))
			{
				leftInclude = mid;
			}
			else
			{
				right = mid;
			}
		}
		return leftInclude;
	}
}

class Solution {
public:
	long long findMaximumNumber(long long k, int x) {
		auto Can = [&](long long mid) {
			const auto numCnt = mid + 1;
			long long llCnt = 0;
			for (int i = x - 1; i < 62; i += x) {
				const long long iUnit = 1LL << (i+1);
				const long long iHalfUnit = iUnit / 2;
				llCnt += numCnt / iUnit * iHalfUnit;
				llCnt += max(0LL, numCnt % iUnit - iHalfUnit);
			}
			return llCnt <= k;
		};
		return NBinarySearch::FindEnd(0LL,
		, Can);

	}
};

使用半周期

namespace NBinarySearch
{
	template<class INDEX_TYPE, class _Pr>
	INDEX_TYPE FindFrist(INDEX_TYPE left, INDEX_TYPE rightInclue, _Pr pr)
	{
		while (rightInclue - left > 1)
		{
			const auto mid = left + (rightInclue - left) / 2;
			if (pr(mid))
			{
				rightInclue = mid;
			}
			else
			{
				left = mid;
			}
		}
		return rightInclue;
	}

	template<class INDEX_TYPE, class _Pr>
	INDEX_TYPE FindEnd(INDEX_TYPE leftInclude, INDEX_TYPE right, _Pr pr)
	{
		while (right - leftInclude > 1)
		{
			const auto mid = leftInclude + (right - leftInclude) / 2;
			if (pr(mid))
			{
				leftInclude = mid;
			}
			else
			{
				right = mid;
			}
		}
		return leftInclude;
	}
}

class Solution {
public:
	long long findMaximumNumber(long long k, int x) {
		auto Can = [&](long long mid) {
			const auto numCnt = mid + 1;
			long long llCnt = 0;
			for (int i = x - 1; i < 63; i += x) {
				const long long iHalfUnit = 1LL << i ;
				long long iUnitCnt = numCnt / iHalfUnit / 2;
				llCnt += iUnitCnt * iHalfUnit;
				llCnt += max(0LL, numCnt - iUnitCnt* iHalfUnit*2 - iHalfUnit);
			}
			return llCnt <= k;
		};
		return NBinarySearch::FindEnd(0LL, 2*k+ 10000, Can);
	}
};

扩展阅读

视频课程

有效学习：明确的目标及时的反馈拉伸区（难度合适），可以先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

我想对大家说的话
闻缺陷则喜是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛