1.非比较排序
我们前面讲的排序算法都是通过比较大小来进行排序的,他们都是比较排序。
像基数排序、计数排序和桶排序等都不是通过比较大小来排序的,是非比较排序,在这里我们讲一下其中的计数排序和基数排序,而桶排序实现起来太挫,是一种类似哈希的结构,我们之后会学到哈希结构,就不学习桶排序了。
1.1计数排序
计数排序是怎么不通过比较两个元素的大小进行排序的呢?假设我们有下面这样一组数据:
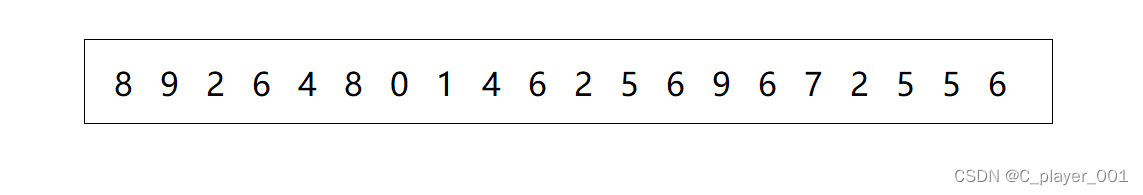
对于这样的数据,我们前面学的排序当然都可以解决,但是这里我们要用一种很巧妙的方法,相信大家在做题的过程中肯定遇见过这样的一类题 : 某个数组包含 0~n 的数据,每一数组都只出现了一次,而有一个数据缺失了,只遍历这个原数组一遍找出这个缺少的数。在做这个题的时候,我们用到了一种方法,就是创建容纳一个 n+1 个整形的数组,用calloc,开辟的时候顺便初始化为0,然后遍历原数组一遍,以原数组的元素作为下标访问 我们开辟的新数组,把该下标位置的0加一变成1。最后遍历一遍用来计数的数组,看哪个下标的元素为0,就代表着这个下标在原数组中没有出现过。而我们计数排序就是通过统计数组中每一个元素出现的个数来进行排序的。
首先我们要创建一个数组来统计个数,我们看到前面的数组的最大值就是9,所以我们就开创一个十个整形大小的数组。
//遍历一遍找最大数
int max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > max)
max = a[i];
}
//创建一个 max+1的数组
int* count = (int*)calloc(max + 1, sizeof(int));
assert(count);第二步就是遍历数组统计次数
//遍历一遍统计个数
for (int i = 0; i < n; i++)
{
count[a[i]]++;
}
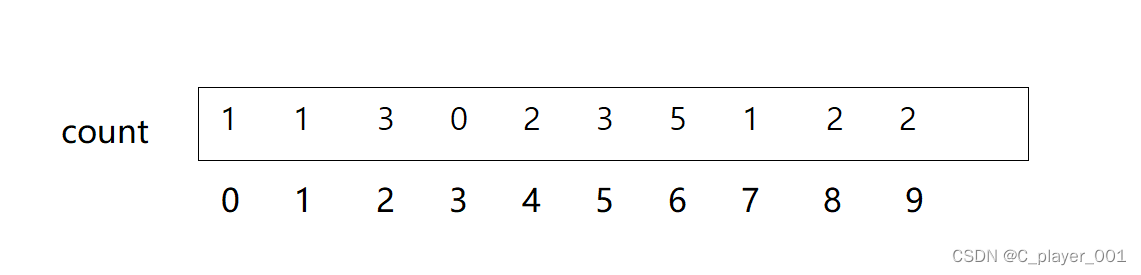
当把每个数出现的次数统计出来之后,我们就看艳照出现的次数将其依次覆盖回原数组。覆盖完之后就已经把元数据排好序了,最后释放掉count数组
int j = 0;
//覆盖回原数组
for (int i = 0; i < max + 1; i++)
{
while (count[i]--)
{
a[j++] = i;
}
}
free(count);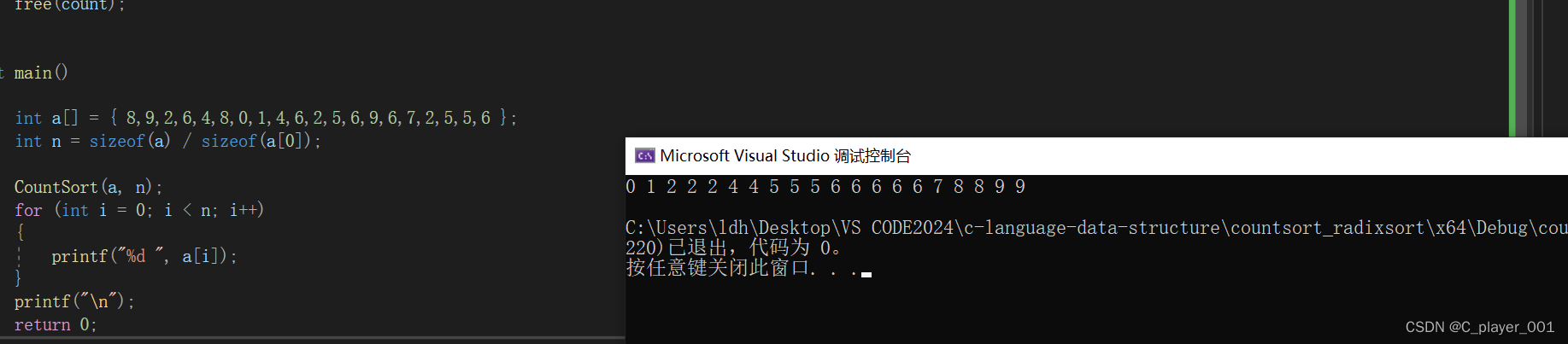
这个算法的思路很简单,同时,我们在统计数组元素个数时,以计数数组的下标来代表元素,这种就是映射,下标的之就代表元素的值,就是绝对映射。
但是对于这样一组数据呢?

他们之中的最大值是120,那是不是意味着我们就要开辟一块容纳 121 个整形的空间呢?如果我们开辟这么大一块空间,那么前面的一百个空间是不是浪费了?而统计的时候我们只会用到后面的二十一块空间。或者说如果要排序下面一个数组:
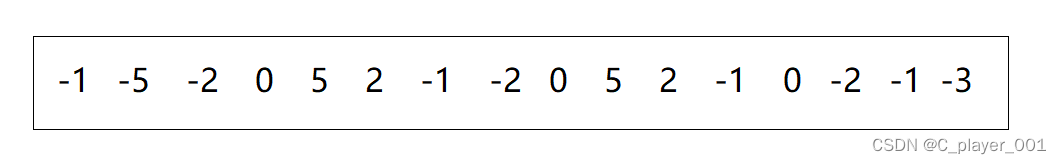
这里的数据有负数,而下标是不可能出现负数,这种情况该怎么处理呢?
这就引申出了第二种思路,相对映射
相对映射具体做法是这样的,我们用 0 下标来代表数组中最小的数据,下标 1 代表最小的数据+1,以此类推。这样一来,我们的计数的数组只要算出数组中的最大值和最小值,他们的差值+1就是我们要开辟的数组要统计的出现次数的数据的个数。
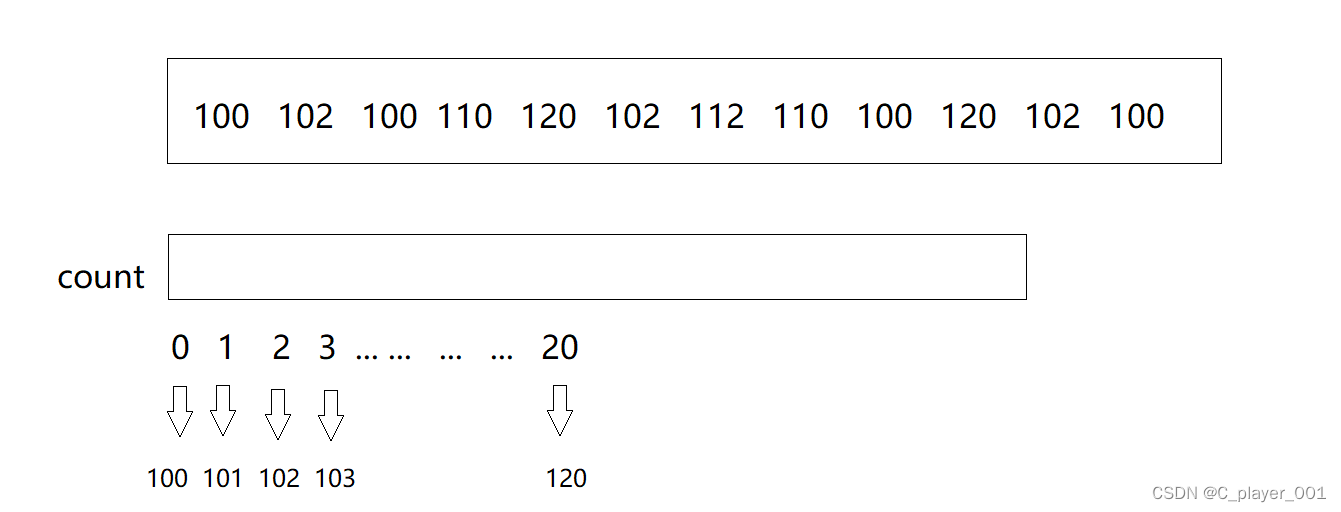
比如第一个数组,我们用0下标来代表100,用1下标来代表101... ...用20下标来代表20,这样一来我们就只要开辟21个整形大小的空间就能完成计数了,大大减小了空间浪费
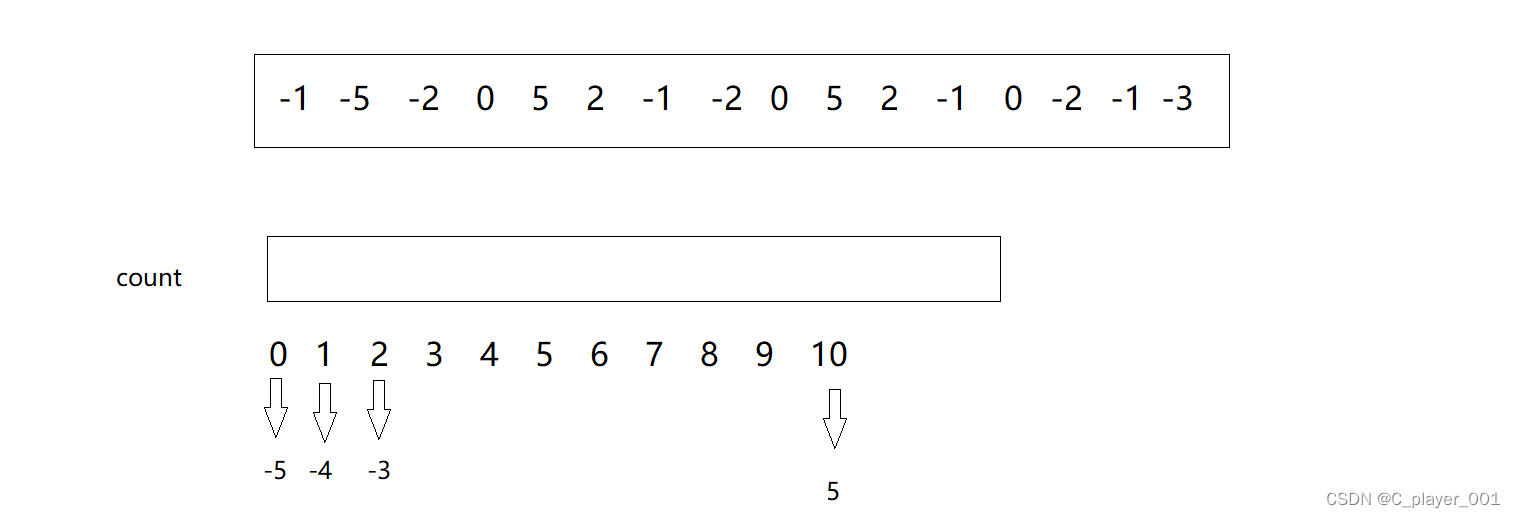
对于存在负数的数组也是一样的,我们用下标 0 来代表最小值 -5,用下标 1 来代表 -4 ... ...用下标 10代表 5 。
这时候我们就可以先遍历一边数组来找出最小值和最大值,然后求出数据范围。其他的操作还是跟之前一样
void CountSort(int* a, int n)
{
assert(a);
int min = a[0];
int max = a[0];
//遍历一遍找最小值和最大值
for (int i = 1; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//求数据个数(范围)
int range = max - min + 1;
//计数数组
int* count = (int*)calloc(range, sizeof(int));
assert(count);
//统计个数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
int j = 0;
//覆盖
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
free(count);
}
相对映射比绝对映射更适合大多数场景。
对于计数排序,适合对数据范围相对集中的数据进行排序,效率很高,只需要遍历两遍数组,O(N+range)的时间复杂度和O(range)的空间复杂度。
他的缺点就是:1.不适合数值分散的数据
2.只适用于整形,不适合浮点数和字符串的排序
字符和负数的排序只要范围相对集中就都能用计数排序进行处理。
1.2基数排序
基数排序其实我们在生活中经常用到,比如打扑克的时候,一张牌的大小取决于它的数值和他的花色,我们对其排序的时候可以先根据他的花色分分组,然后在按其数值进行分组,这样一来政府派的大小就排好序了。
基数排序的思想就是两部:分发数据和回收数据。具体的概念很复杂,但是实现起来其实不是很难。对于基数排序方式有两种:MSD(最高位优先)LSD(最低位优先)
我们直接举例来实现一次基数排序,对于下面的这一组数据

这样的一组数据我们可以根据他的个位十位和百位分别进行分组和回收,这样一来,我们就只有十个分组的基,因为每一位的数值都在0~9之间。
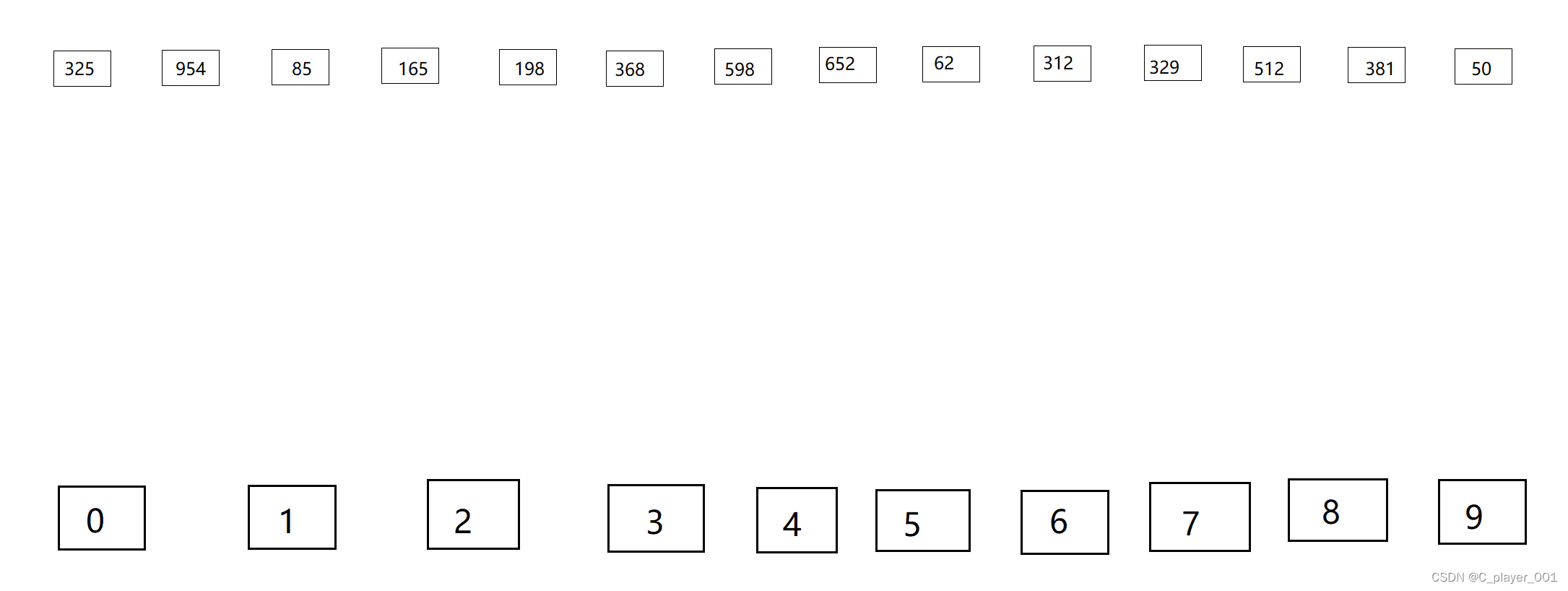
首先我们以个位进行分组
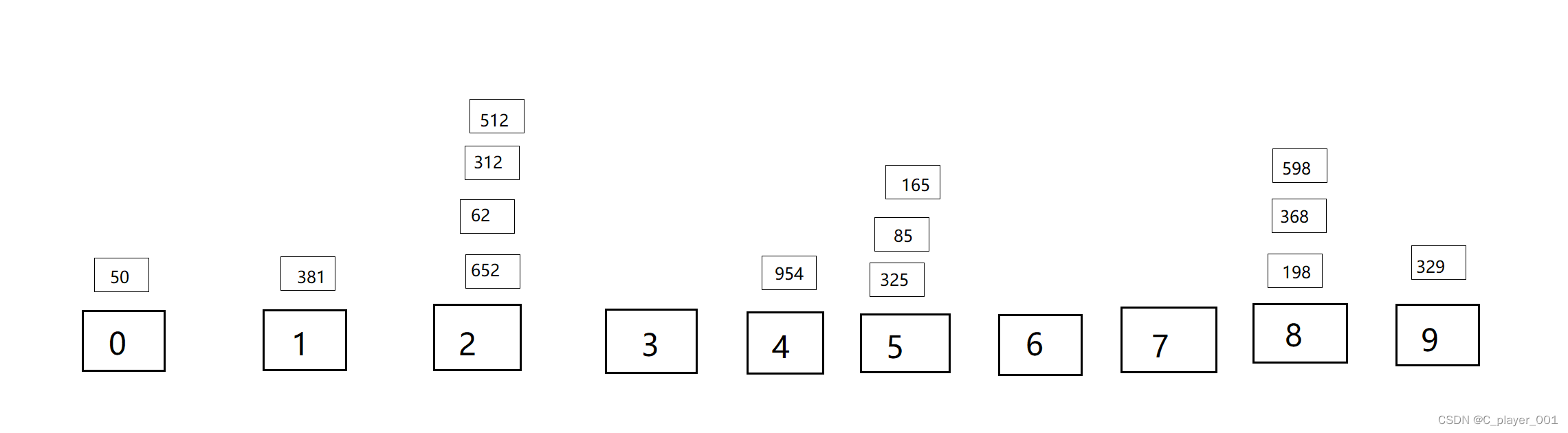
以个位分完组之后进行回收,相同的组里先进来的先出去。

然后再以十位进行分组。
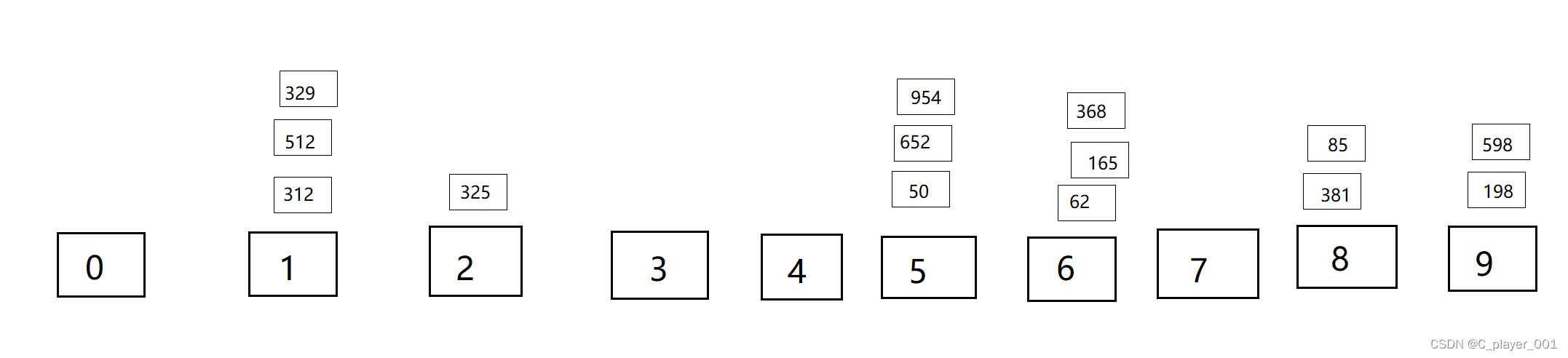
分发完数据之后再进行回收

最后再以百位分发数据
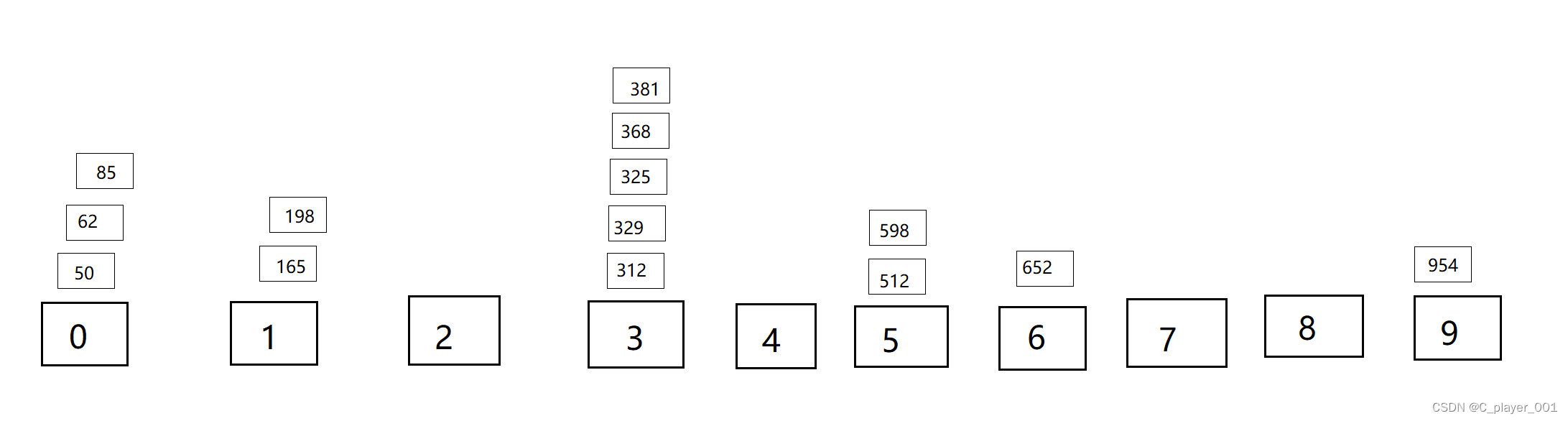
再次回收

这次回收数据之后我们就发现他已经排成有序了,分发和回收数据的次数取决于它的最大的数据有几位。这就是一种基数排序的应用。我们前面说了先进入分组的先出去,这时候我们就可以用队列来实现了。
//分发和回收数据
void Radix(int* a, int n, int k,Queue*q)
{
//先取出每一个数,找到它的那一位,放进相应的队列中
for (int i = 0; i < n; i++)
{
int num = a[i];
int key = 0;
int c = k;
while (c--)
{
key = num % 10;
num = num / 10;
}
//求出他的指定位的数字
//放进指定的队列中
QueuePush(&q[key], a[i]);
}
//回收数据
int j = 0;
for (int i = 0; i < 10; i++)
{
while (!QueueEmpty(&q[i]))
{
a[j++] = QueueFront(&q[i]);
QueuePop(&q[i]);
}
}
}
//主逻辑
void RadixSort(int* a, int n, int k)
{
assert(n);
//k趟分发和回收
Queue q[10];
for (int i = 0; i < 10; i++)
{
QueueInit(&q[i]);
}
for (int i = 1; i <= k; i++)
{
Radix(a, n, i,q);
}
for (int i = 0; i < 10; i++)
{
QueueDestroy(&q[i]);
}
}
排序总结
我们前面学了几种比较排序,这里我们对他们进行一个总结
时间复杂度
直接插入排序:O(N^2)
希尔排序: O(N^1.3)
选择排序: O(N^2)
堆排序: O(NlogN)
冒泡排序: O(N^2)
快排: 最好O(NlogN),最坏O(N^2),但是三数取中优化之后一般不会出现最坏
归并排序: O(NlogN)
空间复杂度
直接插入排序:O(1)
希尔排序: O(1)
选择排序: O(1)
堆排序: O(1)
冒泡排序: O(1)
快排: 最好O(logN),最坏O(N),但是三数取中优化之后一般不会出现最坏
归并排序: O(logN)
除了时间复杂度和空间复杂度,有时候也会关注算法的稳定性。排序算法的稳定性指的是数据中相同的值在经过排序之后,他们的相对顺序不变,如果可以做到相对顺序不变,那就是稳定的排序算法,如果做不到,那就是不稳定的。
稳定性:
直接插入排序:稳定 我们可以控制相同的数不交换位置,这样相对顺序是不会变的
希尔排序:不稳定 我们不知道相同的值被分到了哪个组,分组我们是不可控的,所以希尔排序是不稳定的
选择排序:不稳定 选择排序其实是不稳定的,因为他选数然后交换的时候是无法保证相对顺序一定不变的,就拿下面的数组来举例 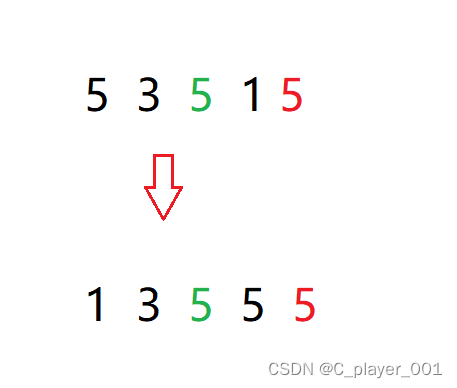
对于这样的数据选择排序是无法保证相对顺序的
堆排序:不稳定 堆排序是经典的不稳定的,他的建堆过程相同的数在不同的子树上就有可能会改变相对顺序,同时,将堆顶元素和最后一个元素交换的时候也是无法保证相对顺序的。比如我们举一个极端例子: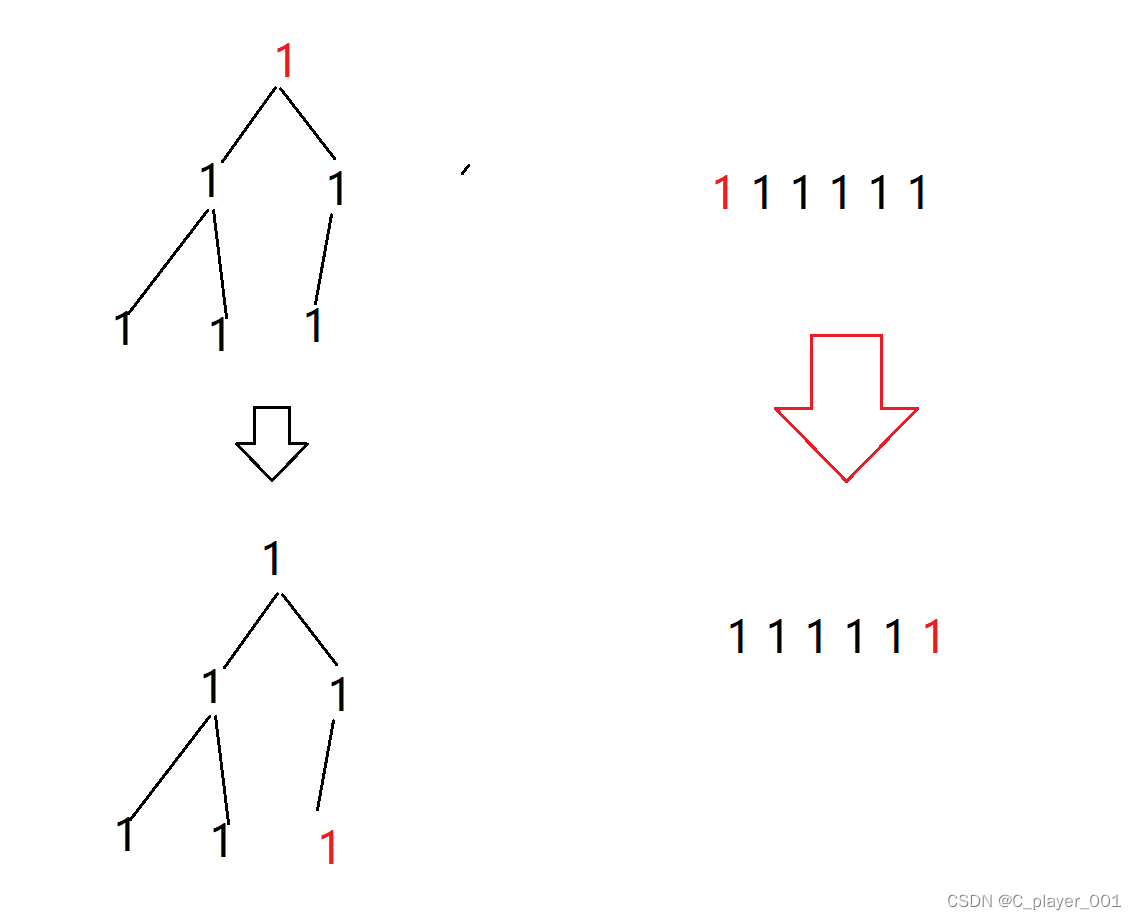
冒泡排序:稳定 冒泡排序我们可以控制他在相等时不交换,这样就能保证不改变相对顺序
快排:不稳定 快排的不稳定体现在 如果key就是那个相等的值,他一趟排序下来的相遇点的位置也就是最终位置是不一定能保证与与之相等的数相对顺序不变的
归并:稳定 归并是分区间排序的,我们可以控相等的时候左边区间的数排在右边区间的前面,这样就能保证相对顺序不变了