用一个寓言故事讲明白KMP算法

在讲寓言故事之前，先讲一下理论的前提知识，避免有些0基础而无法理解

前提知识

首先KMP算法是指在串中，想要快速找出主串里跟我们的模板串一样的位置的一种算法，其主要是解决最普通的BF算法中主串指针回溯的问题。

BF算法就是一个一个比对

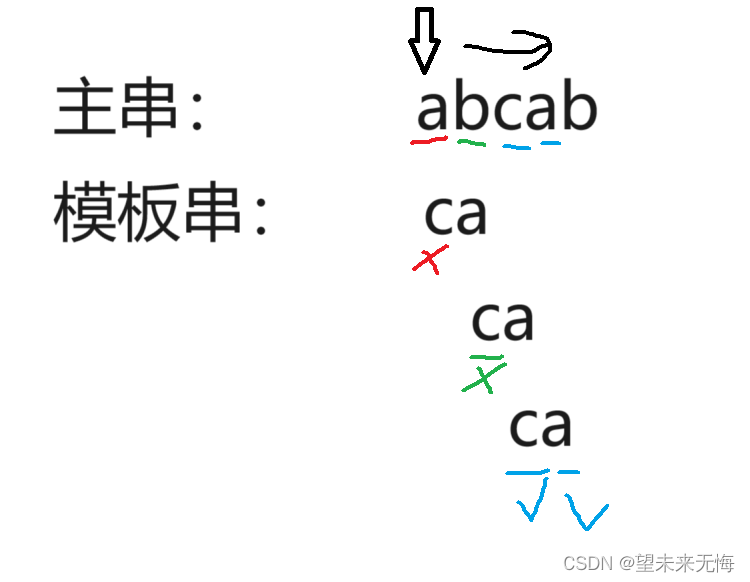
如果主串短还好说，BF算法看起来也不错，但是如果一旦主串长起来，要找的模板串又刚好处于主串的后面，例如主串：abcaabbabcabaacbacba 模板串：abcab，这时再按照BF算法一个一个比对，就会发现有些比对到一半后发现不一样，主串指针又只好回溯到前面去，非常浪费时间。而KMP算法的一个优点就是这个主串指针永远不回溯，要么停着不动，要么前进，没有撤退可言

那什么是KMP算法呢？

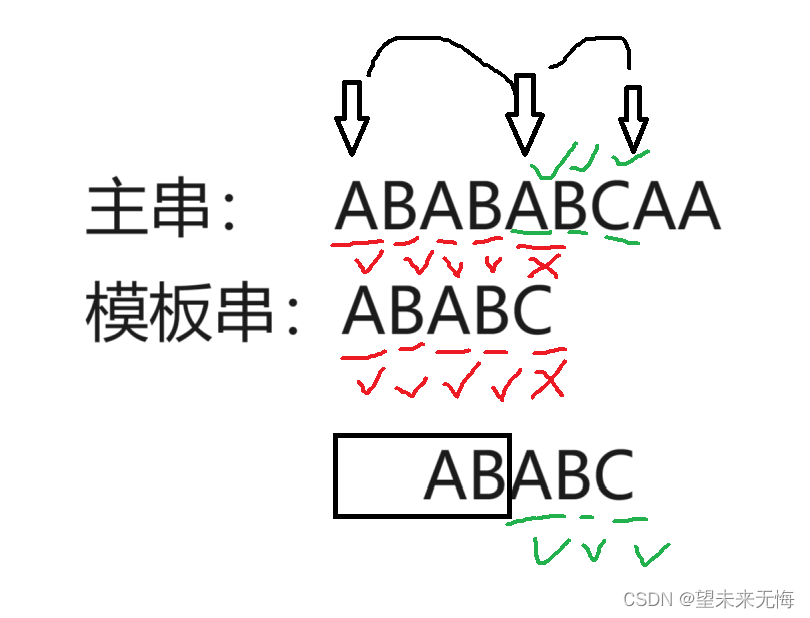
可以看到，KMP算法可以帮助你计算出模板串要右移多少位，然后又从模板串的第几位开始比对，与此同时，主串指针也仍然没有回溯。例如上图，我们比对到模板串的最后一位C时，主串指针也走到了A上，发现不一样，BF算法就会将主串指针回溯到第二位的B上，模板串往右移一位，又开始从头比对，但是KMP算法则会直接告诉你模板串要右移2位，同时，从模板串的第三位开始重新比对，这样一来，效率大大提高。

所以怎么样实现这个功能呢？

这时我们需要一个next数组（KMP算法其实在next数组上有不同的理论，例如同一个模板串ABABC，其中一个说法的next数组对应为01123，而另外一个说法的next数组对应为00120，我们这里以第一个说法为例，虽然方法不一样，但是算法思路都是一样的）

next数组的求法

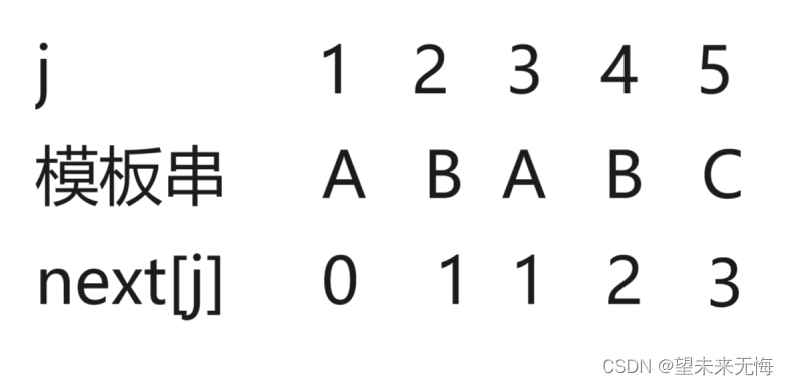
首先大部分做法是：初始化j从1开始，即next[0]我们不用它，其中next[1]我们初始化为0，接下来我们就看当前位之前的模板串中最长前缀后缀重合的字符数再加一

补充（前缀和后缀）：

所以我们可以推出

j=2时,B前面只有A，没有前缀和后缀，即0+1=1

j=3时,A前面有AB，前缀为A，后缀为B，没有重合的前后缀，即0+1=1

j=4时,B前面有ABA，前缀为A,AB，后缀为A,BA，有A这个重合的前后缀，即1+1=2

j=5时,C前面有ABAB，前缀为A,AB,ABA，后缀为B,AB,BAB，有AB这个重合的前后缀，即2+1=3

难点

生成next数组的函数代码

#define MAXLEN 100        //我们创建的结构体
typedef struct
{
    char ch[MAXLEN];
    int len;
}SqString;


void GetNext(SqString t,int next[])
{
    int j,k;           
    j=1;next[1]=0,k=0;     //初始化
    while(j<t.len)          //使每一个数都有对应的next[j]的值
    {
        if(k==0||t.ch[j-1]==t.ch[k-1])
        {
            j++;
            k++;
            next[j]=k;
        }
        else
        {
            k=next[k];
        }
    }

第一眼大多数都看不懂这个代码的逻辑，主要在于这几个关键的代码

一：k==0||t.ch[j-1]==t.ch[k-1]

二：next[j]=k

三：k=next[k]

这时候会很绕，我们先忘记这个代码，讲一个寓言故事，同时KMP算法我们给它换个名字：看门牌算法

寓言故事

从前有一个人，想要努力赚钱，于是他赚啊赚，很快有了一笔存款，同时他想着假如有一天钱突然全亏没了，得留一笔钱作为东山再起的资金，于是他决定，每赚钱赚到一个阶段，他就把一笔钱存进一个房间里，用神秘的门给锁上，这个神秘的门上有一个门牌号，为了避免忘记门在哪里，门上会留有上一次存钱房间的门牌号，同时打开这扇神秘门的条件是，如果未来的他还具备某一样品质，那么这扇门就可以被打开。

许多年后，他成为了一位非常有钱的人，但是在这些年中，为了赚更多的钱，他变得唯利是图，不择手段，贪得无厌，直到有一天，突然出了变故，他所有的钱全部都亏光了，他不认命，想要东山再起，但是呢，他又不想从零开始白手起家，这时他想起以前他给自己存的备用资金，

于是他找到了最近一次存的一扇门，因为是最近一次存的，所以在这扇门里留的资金是非常多的，他想要打开这扇神秘的门，发现打开这扇门的条件是要有善心，但是因为他有钱之后，从不做慈善，只愿意独自享受，所以他无法打开这扇门，但是这扇门上留有再上一次存钱的门牌号，

于是他按照这个门牌号来到了另外一个神秘的门前，但是由于这个门里是更早一段时候存的钱，所以远没有刚刚最近一次的门里存的钱多，他安慰自己至少还有一些钱，这扇门打开要求的是要有诚信，但是他之前为了赚钱，靠坑蒙拐骗赚了许多钱，早就丢失了诚信，所以这扇门他也打不开，

没办法，他只好按照这扇门挂着再上一次存的钱的门牌号去往另外一扇门，他来到这扇门，发现这扇门里存的是他第一次存钱的地方，所以没有再记录上一次的门牌号了，也就是说这是最后一扇门，因为是刚开始赚钱的时候存的，所以这里面的钱很少，他安慰自己，有总比没有好，打开这扇门的条件是要有孝心，可是他赚了钱以后，嫌弃父母是累赘，就再也没有管过父母了，所以这扇门他也打不开，

这时他认命了，发现自己当初为了赚钱，丢失了这么多宝贵的品质，于是他幡然醒悟，决定再次白手起家，东山再起。

寓言故事结束了，这时我们再回到代码中来，我们试图将代码转换为这个寓言故事，进行类比

类比

一：我们模板串比对的时候，如果发现比对错误，我们是不是不想又从头开始比对，如果告诉你我们遍历过的模板串有一个位置可以从这里开始比对，就没必要从头开始比对了

相当于故事里，这个人一直在赚钱，赚了许多钱后，突然全亏光了，他不想从0开始白手起家，如果有一扇神秘的门可以被打开，拿到里面放的备用资金，就没必要从头开始了

二：还记得我们将KMP算法改名为看门牌算法吗，是因为next[j]就相当于一个门牌的作用，如果发现比对错误，我们会找当前位置的next数组的值，然后跳回模板串等于next数组的值的j这个位置，如果这个j对应的字符等于主串指针指向的字符，我们就可以从模板串的这个位置开始比对，如果这个j对应的字符不等于主串指针指向的字符，我们再找这个位置的next数组的值，然后再跳回模板串等于next数组的值的j另外这个位置，如此循环，直到j=1时，其next[j]（门牌号）为0为止

相当于故事里，这个人亏完钱后，按照门牌号的位置，如果能打开这扇门，就能让他东山再起的起点更高，这一扇门如果不行，就找下一扇门，但是越往后存的钱越少，东山再起的起点就越低，但如果找到最后一扇门都打不开，那就只能从0开始了

综上，通俗来讲上面那三行代码的意思

if(k==0||t.ch[j-1]==t.ch[k-1])就相当于故事里他要继续赚钱的条件：

第一个条件就是他亏完钱后，门全部找完了，一扇也打不开，这时再也没有门牌号了，即k==0（因为next[j]==0，按门牌号找j==0的位置不存在）；

第二个条件就是他还没有亏钱，仍然在继续赚钱，越赚越多，即t.ch[j-1]==t.ch[k-1](因为没有发生比对错误，就相当于没有亏钱)

next[j]=k就相当于故事里他每赚钱赚到一定阶段，就要存钱存到一扇门里，即next[j]就相当于赚到一定阶段，=k就相当于留下门牌号

k=k[next]在else里，else就相当于故事里他发生亏钱的事情后，在一扇一扇门找的这个过程，但还没有找到最后一扇门，即k=k[next]代表按照当前找的这一扇门，给的前往下一扇门的门牌号

这时也许就能大概get到这几行代码的逻辑了吧，于是我们最后再用图解法从头理一遍就能完全明白KMP算法了（这里用的是b站的一位up视频里截图，也是他提出的看门牌的名字，寓言故事的灵感也是从这个视频来的，如果想更清晰的了解，可以去原视频里图解法里看看，非常清晰形象http://【KMP算法之求next数组代码讲解】https://www.bilibili.com/video/BV16X4y137qw?vd_source=192e499b6f41fa854f9477bb78ce75c4）

图解法

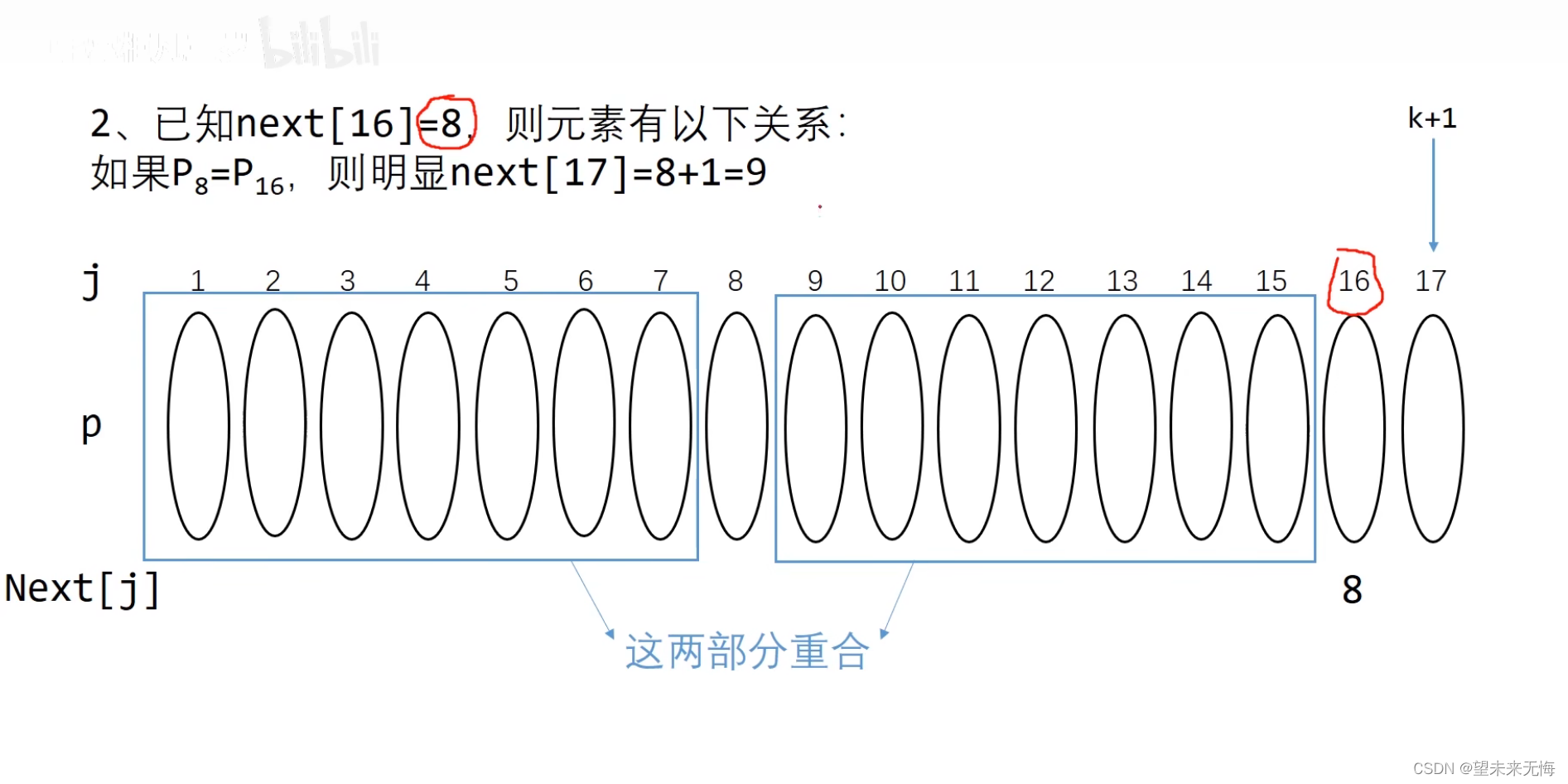
第一步，假设j==16时，他的next[j]==8，就说明了1到7这个前缀和9到15这个后缀重合，如果16等于8，那么next[17]==7+1==8，如果不等于8，这时我们按照看门牌next[16]==8，找到j==8这个位置

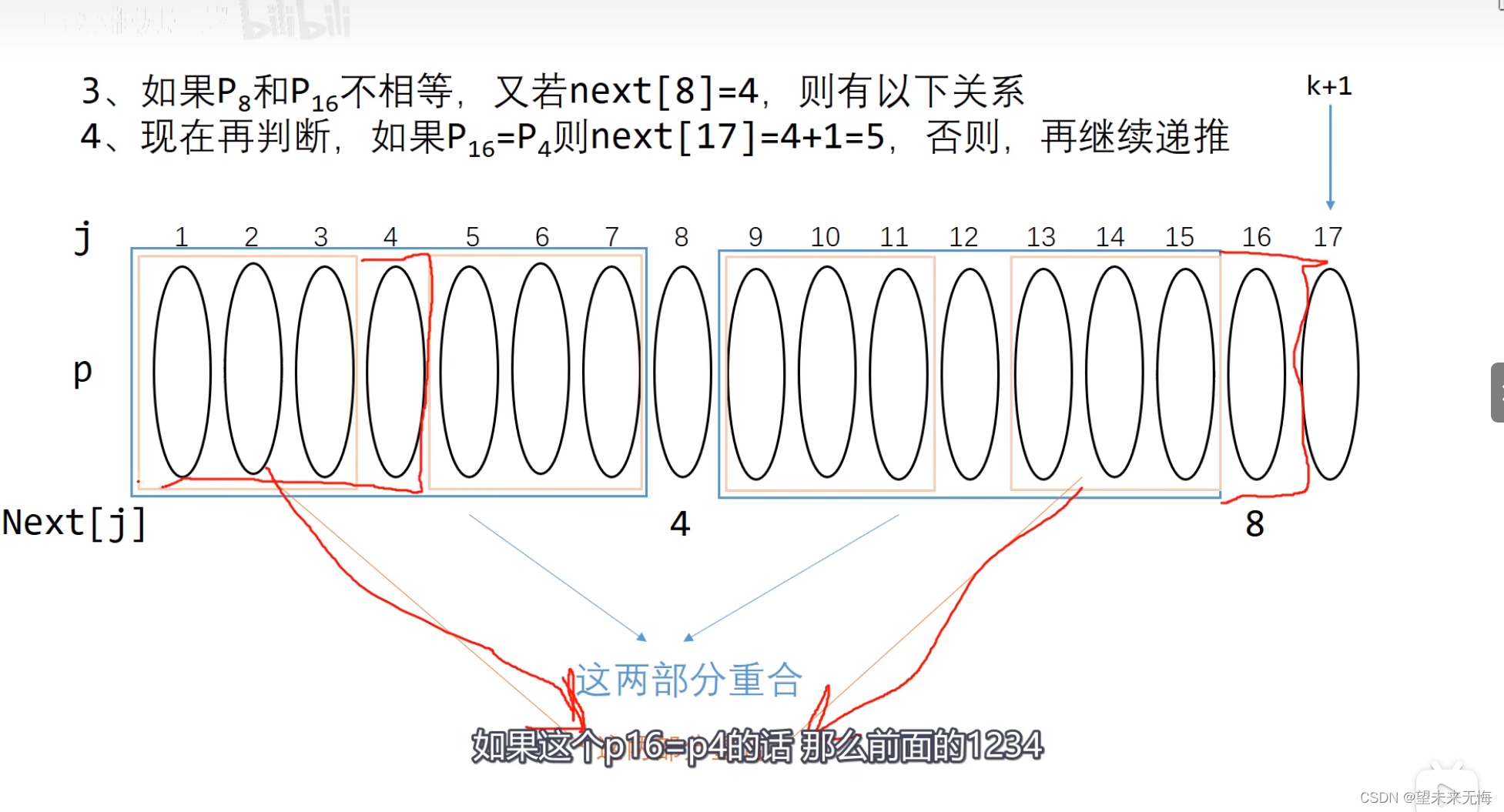
第二步，假设j==8时，他的next[j]==4，就说明1到3这个前缀和5到7这个后缀重合，根据对称性，我们可得另外一个子串中，9到11这个前缀和13到15这个后缀重合，也就是说这四个部分都一样

如果16等于4，那么next[17]==3+1==4，但我们主要想用到1到3和13到15这两个部分，这时我们按照看门牌next[8]==4，找到j==4这个位置

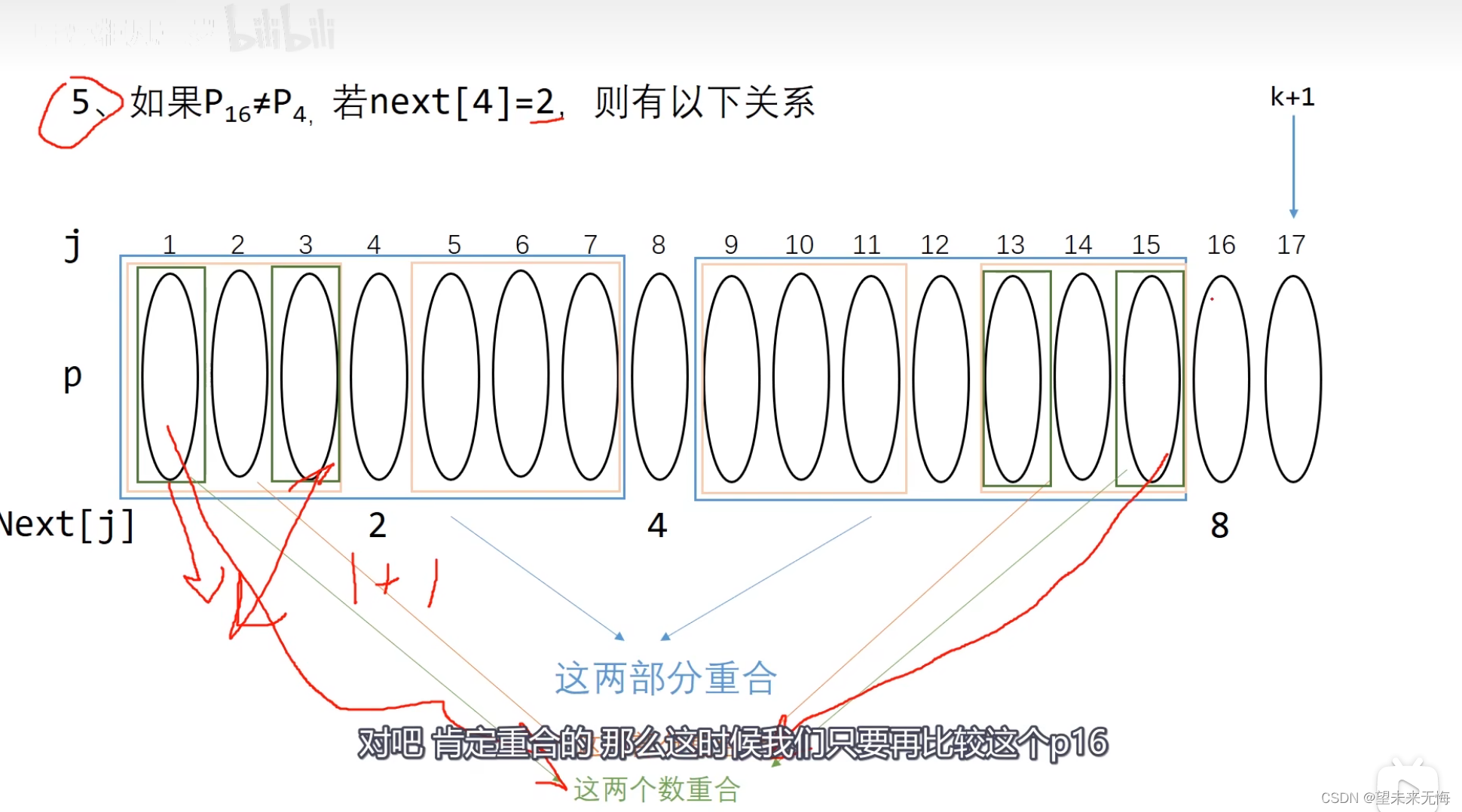
第三步，假设j==4时，他的next[j]==2，就说明1这个前缀和3这个后缀重合，根据对称性我们知道5和7也是重合的，9和11也是重合的，13和15也是重合的，即它们都是同一个字符，如果此时16==2，那么next[17]==2+1==3，如果不等于，我们推断一下就知道next[2]==1，按照看门牌就找到j==1的地方，又因为next[1]==0，所以循环就在此终结了

这时再结合图解联系刚刚类比的寓言故事，我相信大家已经能理解KMP算法了

最后理解了难点：生成next数组之后，实现KMP算法就很简单了

int IndexKMP(SqString S,SqString T)    //S是主串，T是模板串
{
    int next[MAXLEN],i=1,j=1;          //创建next数组，i是主串指针，j是门牌
    GetNext(T,next);                  //生成next数组每一项的值
    while(i<=S.len&&j<=T.len)         //如果主串指针的指向没有超出主串长度并且模板串没有比对完
    {
        if(j==0||S.ch[i-1]==T.ch[j-1])     //如本文所讲的逻辑
        {
            i++;
            j++;
        }
        else
        {
            j=next[j];
        }
    }
    if(j>T.len)        //说明模板串比对完了
    {
        return (i-T.len);        //返回主串中模板串对应的起始下标
    }
    else          //没找到
    {
        return 0;       
    }
}