Conditional Physics-Informed Graph Neural Network for Fractional Flow Reserve Assessment
Authors: Baihong Xie, Xiujian Liu, Heye Zhang, Chenchu Xu, Tieyong Zeng, Yixuan Yuan, Guang Yang, and Zhifan Gao
Source: MICCAI 2023

Abstract
血流储备分数 (FFR) 的评估对于诊断冠状动脉疾病和确定需要重建的患者和病灶非常重要。深度学习已成为评估 FFR 的一种有前途的方法,因为与计算流体动力学相比,它在计算效率方面具有优势。然而,它缺乏适当的先验知识。目前的研究仅考虑将先验知识添加到损失函数中,这仍然不足以学习具有强关联边界条件的特征。在本文中,提出了一种基于条件物理学知识图神经网络 (CPGNN),用于具有形态和边界条件信息的 FFR 评估。具体而言,CPGNN 将形态和边界条件添加到输入中,以学习条件化特征,并将物理方程和边界条件的残差包括在损失函数中。此外,CPGNN 由一个多尺度图融合模块 (MSGF) 和一个物理知识损失组成。MSGF 用于生成由冠状动脉拓扑约束的特征,更好地表示不同范围的依赖关系。物理知识损失使用有限差分法计算物理方程的残差。CPGNN 在来自 143 个 X 射线和 40 个 CT 造影的 183 个真实冠状动脉上进行了评估。CPGNN 的 FFR 值与 FFR 测量值相关性较高,X 射线中的相关系数 r = 0.89,CT 中的相关系数 r = 0.88。
Background
血流储备分数(FFR)的评估对于诊断冠心病(CAD)和确定需要血管重建的患者和病灶具有重要意义。尽管CAD通常通过血管造影技术在常规中进行诊断,但解剖标志通常低估或高估病变的功能严重性。FFR是CAD功能诊断的金标准,并指导血管重建策略,因为它能够评估狭窄的缺血潜力。根据一项多中心试验,使用FFR可以提醒需要血管重建的严重狭窄的额外30%。此外,另一项试验显示通过使用FFR可将1年不良事件率降低5.1%。因此,欧洲心脏学会和美国心脏协会的临床实践指南倡导在临床实践中常规使用FFR。然而,广泛采用FFR受制于在冠状动脉内操纵压力导丝的风险以及评估多个血管所需的时间增加。因此,迫切需要从血管造影中推导FFR。
在这篇论文中,作者将先验概念应用于输入层。通过将边界条件作为先验加到输入中,学习到的特征与边界条件建立了紧密的关联,使得特征中蕴含了更直接且强有力的边界条件信息。同时,为了确保 coronary 的拓扑结构约束,论文引入了图网络作为先验,因为图中的节点交互与 coronary 上空间点之间的FFR交互相似。
因此,研究者提出了条件物理感知图神经网络(CPGNN),它在形态学和边界条件的限制下进行FFR评估。CPGNN除了在损失函数中加入物理方程和边界条件的约束,还通过将形态学和边界条件作为输入的先验来学习条件特征。特别地,CPGNN包含一个多尺度图融合模块(MSGF)和物理感知损失。MSGF的主要目标是生成受冠状动脉拓扑结构约束的特征,并更好地捕捉不同范围的依赖性。物理感知损失则利用有限差分方法计算物理方程的残差。
该论文的主要贡献有三点:
1. CPGNN在形态学和边界条件的条件下提供FFR评估。
2. CPGNN通过将形态学和边界条件信息整合到输入,以及设计多尺度图融合模块,捕捉与这些信息相关的条件特征。
3. 通过6600个合成冠状动脉和183个包括40个CT和143个X射线的临床数据的广泛实验,CPGNN的表现证明了其相较于现有六种方法的优势。
Method
问题陈述:
CPGNN 的目标是通过添加适当先验,确保血压和流量预测符合边界条件和物理原理。它试图寻找一个描述血压和流量规则的损失函数。利用血流动力学理论,设计了一个神经网络 \( Q^\omega(z) \) 和 \( P^\omega(z) \) 来近似在空间坐标 \( z \) 上的血压和流量,该网络遵循给定的控制方程 \( F \) 和边界约束 \( B \)。
CPGNN 详细方法:
- 架构:CPGNN 采用编码-解码架构,输入包括形态参数 \( \theta \) 和边界条件 \( \gamma \)。多尺度图融合用来确保遵循冠状动脉的拓扑结构并捕捉不同范围的依赖性。通过物理信息指导特征编码。
- 特征编码:将形态参数 \( \theta \) 直接与空间坐标 \( Z \) 结合,利用1D卷积和下采样生成形态特征 \( M(z|\theta) \)。边界条件 \( \gamma \) 通过全连接层嵌入为 \( B(\gamma) \)。
- 多尺度图融合:使用图卷积操作来约束血管结构,将 \( M(z|\theta) \) 构成图,同时将 \( B(\gamma) \) 作为边界点添加。多尺度机制用于增强特征表示。
- 特征解码:通过1D卷积和上采样,将 \( Hp(z|\theta, \gamma) \) 解码为压力预测 \( P(z|\theta, \gamma) \),并且考虑到质量守恒,同一分支上的点共享预测。通过全连接层解码 \( Hq(z|\theta, \gamma) \) 为流预测 \( Q(z|\theta, \gamma) \)。
- 损失函数:Momentum Loss(动量损失)、Junction Loss(节点损失)和Boundary Loss(边界损失)分别结合了动力学方程、节点守恒和边界条件。总损失 \( L_{total} \) 为这些部分的和,通过平衡参数 \( \lambda_1 \) 和 \( \lambda_2 \) 调整。
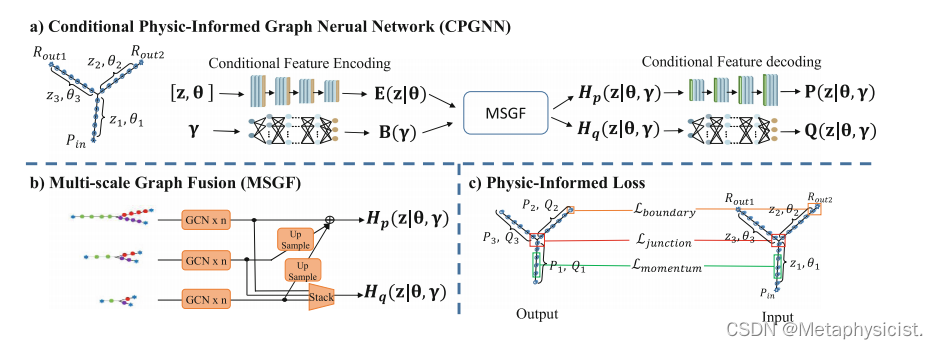
图1。CPGNN的架构。形态学θ和边界γ被添加到输入值中。采用多尺度图融合来加强冠状动脉拓扑结构的约束,并捕获不同范围的依赖性。物理提示损失用于指导条件特征编码

图2。具有代表性的压力预测表明,我们的CPGNN在x射线血管造影数据上优于其他最先进的方法
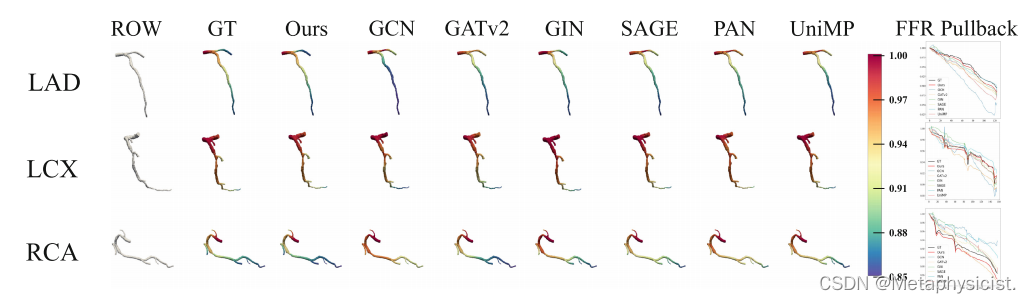
图3。具有代表性的压力预测表明,我们的CPGNN在CT数据上优于其他六种最先进的方法。
Results
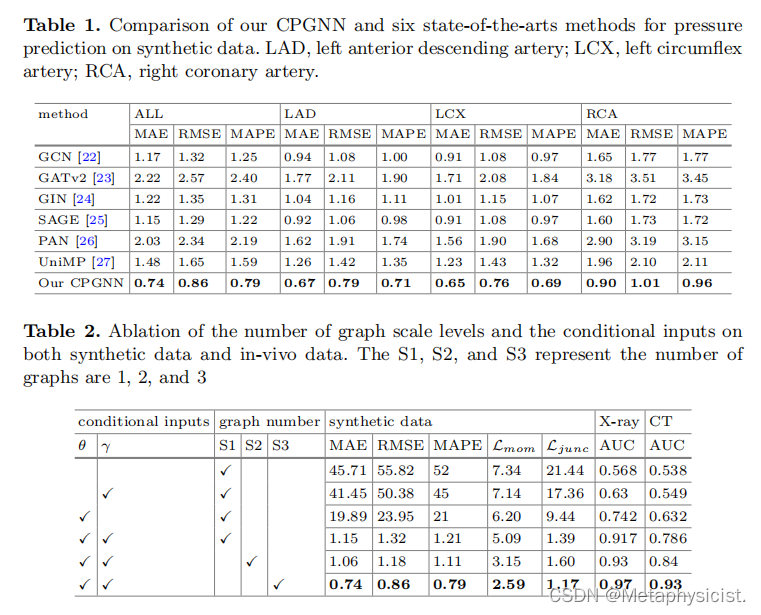
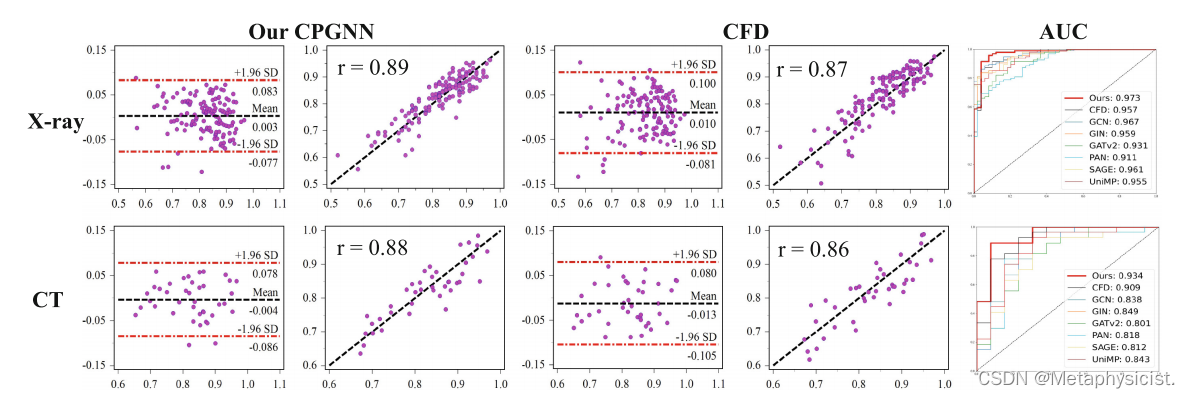
图4。比较CPGNN与计算流体动力学(CFD)的FFR评估。GT是体内FFR测量。对CPGNN和CFD均进行了Bland-Altman分析和皮尔逊相关分析。采用CPGNN、CFD的曲线下面积(AUC)和六种最先进的狭窄诊断方法(FFR<0.8)
1. 实验材料与设置:
- 合成数据集:生成了6600个用于训练的合成冠状动脉模型,参数包括血管半径、长度、分支数量、入口压力和出口阻力,压力真实值由Simvascular模拟。
- 实体数据集:包含143个X射线和40个CT血管造影图像,来源于183名患者的临床数据,边界条件基于TIMI计数法和PP-outlet策略,使用Abbott的HI-TORQUE压力导丝进行FFR测量。
2. 结果:
- 合成数据结果:CPGNN在压力预测方面的表现优于其他六种方法,以0.74的平均绝对误差(MAE)、0.86的均方根误差(RMSE)和0.79的平均绝对百分比误差(MAPE)接近真实值。
- 条件输入与多尺度机制的分析:CPGNN在没有形态学和边界条件输入时,性能较差。引入这些条件后,性能显著提升,表明这些先验信息是关键。
- 实体数据结果:在FFR评估中,CPGNN与实体测量值的Bland-Altman分析和皮尔逊相关系数显示良好的一致性。对于FFR诊断,CPGNN的AUC优于其他方法。
结论:
- 研究提出了CPGNN,一种在形态学和边界条件下进行FFR评估的图神经网络。相较于当前的简化计算方法,CPGNN不需要额外的stenosis检测算法,能自动提取特征,避免了误差累积并展现出更好的性能。
- CPGNN通过将形态学和边界条件信息作为输入,并利用多尺度图融合模块,有效捕捉相关特征,尤其在临床数据上的FFR评估中表现出优势。
- CPGNN在X射线和CT数据上的FFR关联度高(r = 0.89 和 r = 0.88),且计算速度比SimVascular方法快600倍,对于临床FFR评估具有重要辅助作用。
Reference
[1] Xie, B., Liu, X., Zhang, H., Xu, C., Zeng, T., Yuan, Y., ... & Gao, Z. (2023, October). Conditional Physics-Informed Graph Neural Network for Fractional Flow Reserve Assessment. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 110-120). Cham: Springer Nature Switzerland.