目录
题外话
正题
选择排序
选择排序思路
选择排序代码详解
选择排序复杂度
双向选择排序
双向选择排序思路
双向选择排序代码详解
堆排序
堆排序思路
堆排序代码详解
堆排序复杂度
冒泡排序
冒泡排序思路
冒泡排序代码详解
冒泡排序复杂度
小结
题外话
今天状态超级好,废话不说直接写博客!!
先说下,我会尽力将博客中的各种问题,通过文字和图形和代码结合的方式让大家更直观清晰的去理解,毕竟写博客不是看视频,我只能尽量让大家明白这些知识
想学的人自然会去琢磨,不想学的人你就喂到他嘴里,他都不想咀嚼一下
正题
上篇我们写完了直接插入排序和希尔排序,让我们继续写排序内容
选择排序
选择排序思路
创建i和j
i从0下标开始,j从i+1开始
j在数组中寻找剩余元素的最小值
找到之后把最小值和i交换
循环此过程,直到i走到数组倒数第1个元素结束,倒数第一个元素不需要再排序,因为前面都排序完成,最后一个肯定是有序的
觉得上面讲的不清晰可以看下图

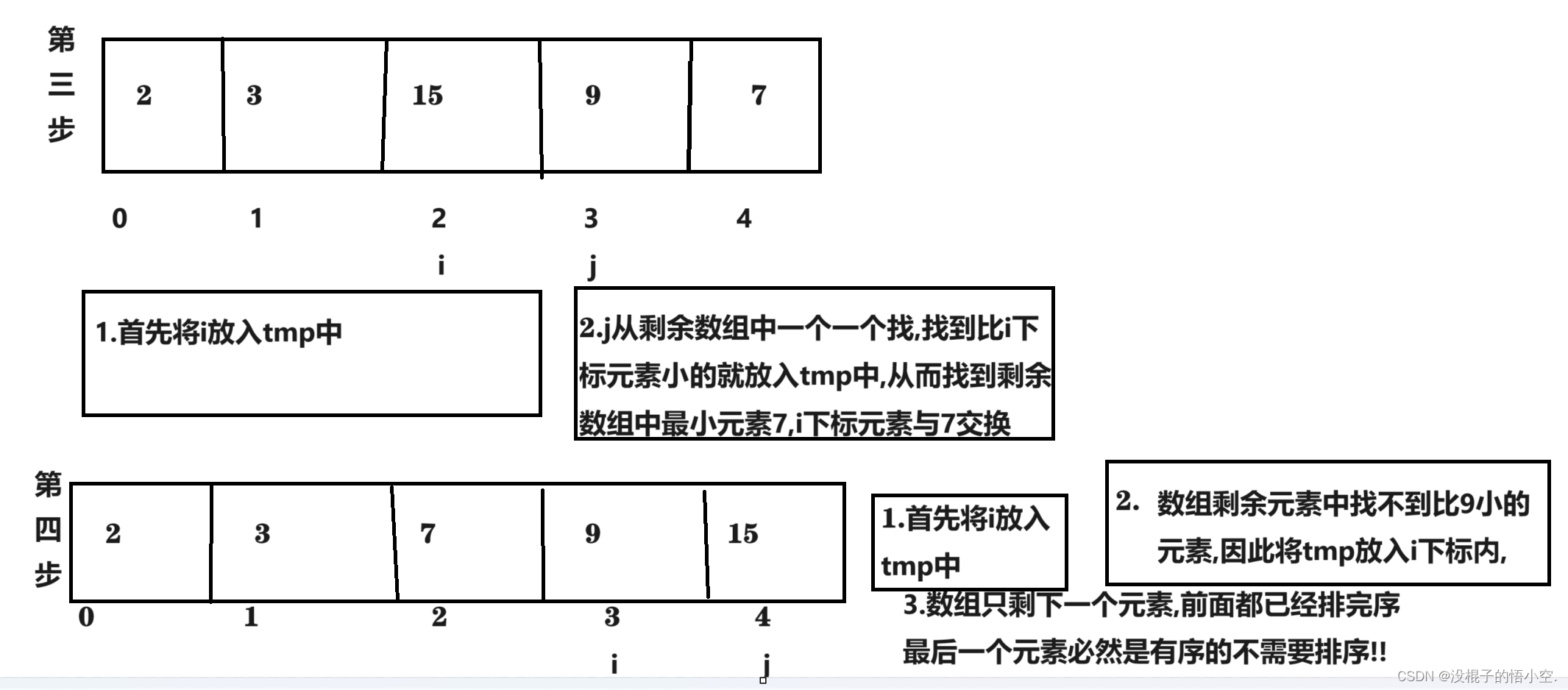
选择排序代码详解
public void selectSort(int[] arr)
{
//创建tmp作为临时变量,swap作为交换变量
int tmp;
int swap;
//i从0下标开始,i走到倒数第二个元素排完序就结束,最后一个元素必然有序!!
for (int i=0;i<arr.length-1;i++) {
//tmp是记录最小元素下标值,先将i下标放入tmp中
tmp=i;
//j下标就等于i+1
int j = i + 1;
//j每趟肯定是从i+1开始到数组最后一个元素结束
for (; j <arr.length; j++) {
//当tmp中元素大于j中元素,就说明tmp不是剩余数组中最小的元素
if (arr[tmp] > arr[j]) {
//将j下标传给tmp
tmp = j;
}
}
//如果i==tmp说明i此时就是剩余数组元素中最小的,不需要再交换位置
//否则再交换位置
if(i!=tmp)
{
swap = arr[tmp];
arr[tmp] = arr[i];
arr[i] = swap;
}
}
}
选择排序复杂度
时间复杂度:O(n^2)无论数组是否有序,i都会从0下标开始到arr.length-2下标结束
j总共会走n-1,n-2,n-3,.......1,相当于等差数列,所以计算出来为O(n^2)
空间复杂度:O(1),因为就一个数组
稳定性:不稳定,相同元素的位置可能会改变
双向选择排序
上面属于是单向的选择排序,下面我们说说另一个版本双向选择排序
双向选择排序思路
1.创建left,right两个变量,让left从0下标开始向后面走,让right从arr.lenght-1开始向前面走
2.创建minIndex,和maxIndex两个变量,并把left下标传给这两个变量
3.i从letf+1下标往后走,如果遇到比minIndex小的下标元素,就把i下标传给minIndex
4.如果遇到比maxIndex大的下标元素,就把i下标传给maxIndex
5.最后minIndex中的元素一定是剩余数组中最小的元素,maxIndex中的元素一定是剩余数组中最大的元素
6.将minIndex中的元素与left交换,maxIndex中的元素与right交换
7.left++,right--,循环上述过程,最后数组实现从小到大排序
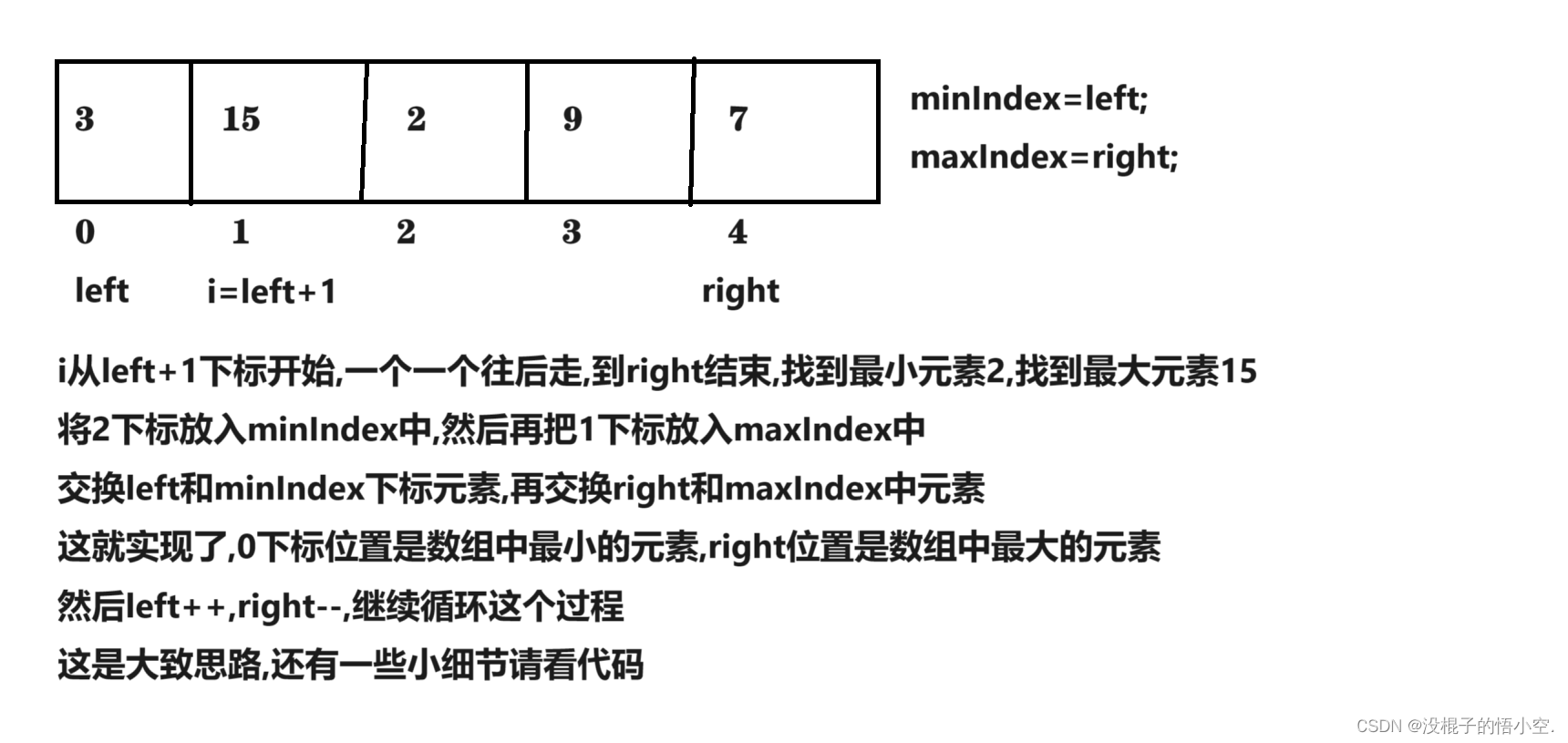
注意!!! 如下图

双向选择排序代码详解
public void DoubleSelectSort(int[] arr)
{
//创建left让其指向0下标
int left=0;
//创建right让其指向arr.length-1下标
int right=arr.length-1;
//left等于right说明排序已经结束,所以left小于right
while (left<right) {
//创建minIndex和maxIndex每次循环将left传给他们
int minIndex=left;
int maxIndex=left;
//i从left+1开始,每趟到right结束,一定要包括right所以i小于等于right
for (int i = left + 1; i <= right; i++) {
//如果遇到i下标元素值小于minIndex下标元素值,说明minIndex不是剩余数组元素最小值,将i传给minIndex
if (arr[i] < arr[minIndex]) {
minIndex = i;
}
//如果遇到i下标元素值大于maxIndex下标元素值,说明maxIndex不是剩余数组元素最大值,将i传给maxIndex
if (arr[i] > arr[maxIndex]) {
maxIndex = i;
}
}
//将最小值和left交换
swap(arr,left,minIndex);
//如果maxIndex==left的话,而且left在上面已经和minIndex交换了
if (maxIndex==left)
{
//我们需要将left交换的mainIndex传入maxIndex,这样maxIndex才是我们需要的
maxIndex=minIndex;
}
//将最大值和right交换
swap(arr,right,maxIndex);
//left往前继续排序
left++;
//right往后继续排序
right--;
}
}
//下标元素交换代码
public void swap(int[] arr,int a,int b)
{
int tmp=arr[a];
arr[a]=arr[b];
arr[b]=tmp;
}
堆排序
堆排序思路
1.先向下调整创建大根堆
2.堆排序,创建好的大根堆,堆顶元素和最后一个没有交换过位置的元素交换位置,然后将没有交换位置的元素,再向下调整成大根堆,然后循环这个过程
之前在堆的那篇博客中讲过堆排序这里就不说太多
堆排序代码详解
//建立大根堆
private void creatHeap(int[] arr)
{
//父亲结点从最后往上依次建立大根堆
for (int parent=(arr.length-1-1)/2;parent>=0;parent--)
{
//向下调整成大根堆
siftDown(arr,parent,arr.length);
}
}
//向下调整
private void siftDown(int[] arr,int parent,int len)
{
//找到孩子节点
int child=parent*2+1;
//孩子节点一定不能超过数组元素数量
while (child<len)
{
//孩子结点+1也不能超过数组元素数量并且child下标元素小于child+1下标元素
if (child+1<len&&arr[child]<arr[child+1])
{
//child++,child指向孩子中最大的那个
child++;
}
//如果孩子中最大的那个大于父亲结点
if (arr[child]>arr[parent])
{
//交换父亲和孩子结点的位置
swap(arr,parent,child);
//继续向下调整
parent=child;
child=parent*2+1;
}else
//如果孩子中最大的不大于父亲结点则说明建立成大根堆,直接退出
{
break;
}
}
}
//从小到大排序,堆排序
public void heapSort(int[] arr)
{ //创建成大根堆
creatHeap(arr);
//从最后一个结点开始
int end=arr.length-1;
//当end>0的时候
while (end>0) {
//交换堆顶元素和最后一个元素位置,这样end位置会是整个堆最大的元素
swap(arr,0,end);
//向下排序,把除去end下标的往后元素,建立成大根堆
siftDown(arr,0,end);
//end--继续循环
end--;
}
}
堆排序复杂度
时间复杂度:O(n*logn),
建立大根堆时间复杂度为O(n),
而堆排序交换堆顶元素和最后一个没有交换元素的位置(交换n次)并且要向下调整为大根堆(相当于根的深度也就是logn),时间复杂度为O(nlogn)
所以时间复杂度为O(nlogn)
空间复杂度:o(1),就一个数组
稳定性:不稳定,相同元素的位置可能会改变
冒泡排序
冒泡排序思路
1.如果相邻的两个元素,前面的大于后面的元素,那么就把这两个元素调换位置
2.继续往后走,按照以上的方式进行循环,可以保证每一趟最后一个元素一定是数组中最大的元素
3.n个元素要走n-1趟
上面看不懂请看下图
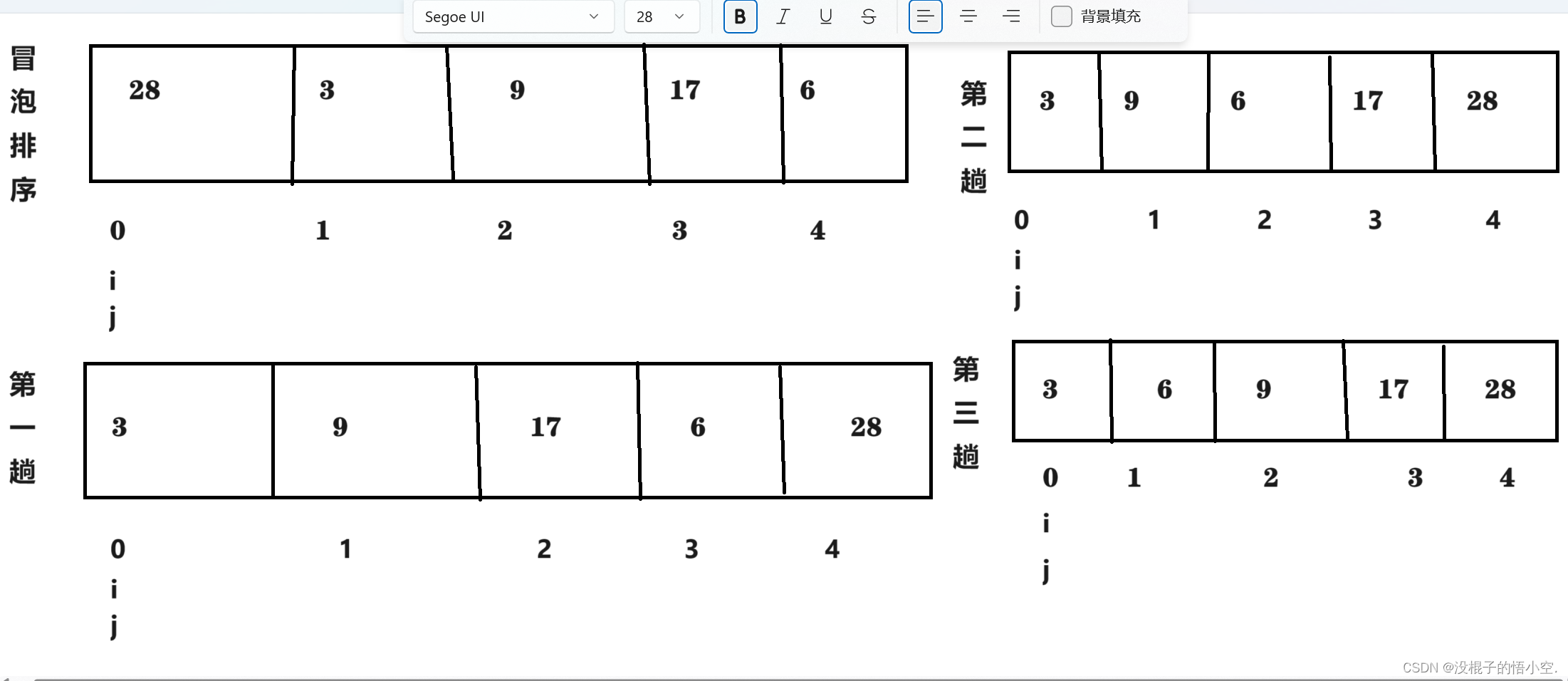
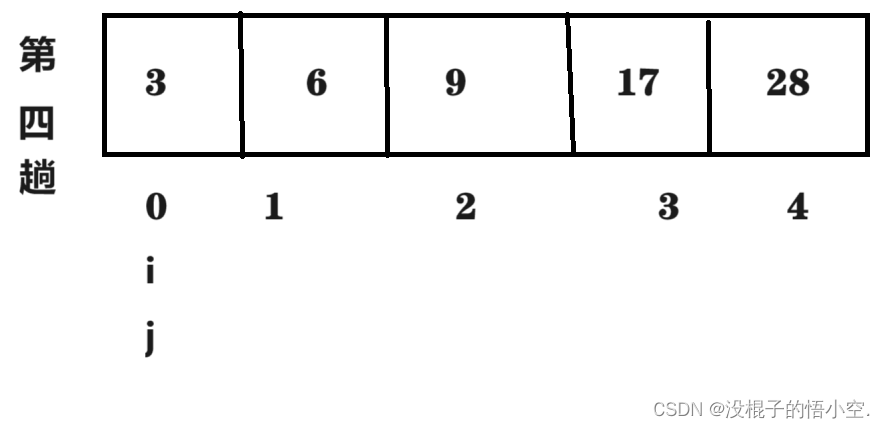
冒泡排序代码详解
public void bubbleSort(int[] arr)
{
//i为趟数,n个元素只需要n-1趟
for (int i=0;i<arr.length-1;i++)
{//创建一个flg将false传入
boolean flg=false;
//莓走完一趟,最后一个元素一定为最大值,最后一个元素不需要再交换
for (int j=0;j<arr.length-1-i;j++)
{
//如果相邻元素前面的比后面的大
if (arr[j]>arr[j+1])
{
//交换两个元素位置
swap(arr,j,j+1);
//如果交换顺序了,就把flg变为true
flg=true;
}
}
//如果!flg为true则说明没有交换顺序,也就说明数组已经有序了,不需要再进行排序
if (!flg)
{
break;
}
}
}
冒泡排序复杂度
时间复杂度:O(n^2),j需要进行n+n-1+n-2+n-3......1次比较,等差数列,时间复杂度为O(n^2)
空间复杂度:O(1),就一个数组
稳定性:稳定,无论怎么交换顺序,相同的元素位置不会改变
小结
没想到会写这么久,画图还有逻辑梳理真的很需要时间,喜欢的家人们麻烦给我个三连(点赞关注收藏!!!!)
求求了!!
博主有不好的地方请在评论区留言或者私信,我都会虚心接受!!!