4 差商与牛顿插值

差商

如果采取间隔不等的采样，差商会变得稍显复杂，对于$x_0,x_1,\dots ,x_n$，若与$y_0,y_1,\dots ,y_n$通过映射$f$一一对应，则定义比值

$$f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0}$$

为$f(x)$关于节点$x_0,x_1$的一阶差商。

由于在计算二阶差商的时候，不可避免地涉及到3个点，所以二阶差商定义为

$$f[x_0,x_1,x_2]=\frac{f[x_0,x_2]-f[x_0,x_1]}{x_2-x_1}$$

$k$阶差商定义为

$$f[x_0,x_1,\dots ,x_k]=\frac{f[x_0,x_1,\dots ,x_{k-2},x_k]-f[x_0,x_1,\dots ,x_{k-1}]}{x_k-x_{k-1}}$$

若将$k$阶差商展开，则可表示为函数值$f(x_0),f(x_1),\dots ,f(x_k)$的线性组合，且每一项的分母必可写为$k$个$x_i-x_j$的乘积，可以表示为

$$f[x_0,x_1,\dots ,x_k]=\sum _{j=0}^k\frac{f(x_j)}{(x_j-x_0)\dots (x_j-x_{j-1})(x_j-x_{j+1})\dots (x_j-x_k)}$$

其中第$j$项的分母中不存在$x_j-x_j$。则

$$\begin{array}{rl}f[x_0,\dots ,x_{k-1}]& =\sum _{j=0}^{k-1}\frac{f(x_j)}{(x_j-x_0)\dots (x_j-x_{j-1})(x_j-x_{j+1})\dots (x_j-x_{k-1})}\\ f[x_1,\dots ,x_k]& =\sum _{j=1}^k\frac{f(x_j)}{(x_j-x_1)\dots (x_j-x_{j-1})(x_j-x_{j+1})\dots (x_j-x_k)}\end{array}$$

易得

$$f[x_0,x_1,\dots ,x_k]=\frac{f[x_1,x_2,\dots ,x_k]-f[x_0,x_1,\dots ,x_{k-1}]}{x_k-x_0}$$

根据这个表达式，可以通过一个简单的递归程序计算数组的差商

# 差商算法,x,y为同等长度的数组
diffDiv<-function(x,y){
    end = length(x)
    ind = 2:end #索引
    return(
        if(end==1) y[1]
        else (diffDiv(x[ind],y[ind])
            -diffDiv(x[ind-1],y[ind-1]))/(x[end]-x[1])
    )
}

如果要计算阶数为k的差商，只需重复调用diffDiv，

kDiffDiv <- function(x,y,k){
    len <- length(x)
    if(len<k) return(0)
    d<-rep(0,len-k)
    for(i in 1:(len-k))
        d[i] <- diffDiv(x[i:(i+k)],y[i:(i+k)])
    return(d)
}

据此，绘制出$y=x^5$这个函数的差商，

> plot(x,y)
> k = 1
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="red")
> k = 2
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="green")
> k = 3
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="blue")
> k = 4
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="purple")
> k = 5
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="yellow")
> k = 6
> lines(x[1:(end-k)],kDiffDiv(x,y,k),col="gray")

如图所示

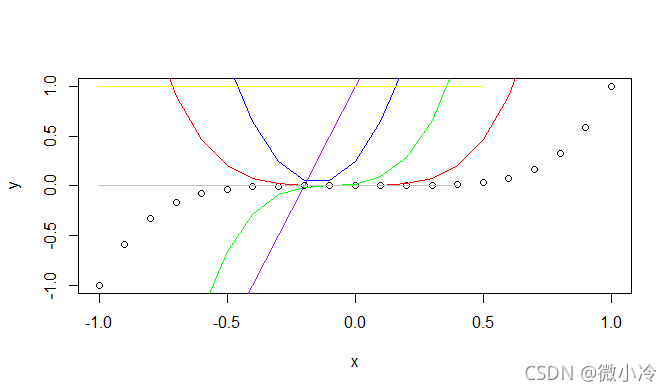
牛顿插值

可见差商与微分在阶数上有着一致的趋势。那么，知道了差商之后，可以做点什么呢？

根据差商定义，可得

$$\begin{array}{rl}f(x)& =f(x_0)+f[x,x_0](x-x_0)\\ f[x,x_0]& =f[x_0,x_1]+f[x,x_0,x_1](x-x_1)\\ & ⋮\\ f[x,x_0,\dots ,x_{n-1}]& =f[x_0,x_1,\dots ,x_n]+f[x,x_0,x_1,\dots ,x_n](x-x_n)\end{array}$$

可见，通过差商可以逼近函数的真实值，将上式合并可得

$$\begin{array}{rl}f(x)=& f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)\\ & +\dots +f[x_0,x_1,\dots ,x_n](x-x_0)(x-x_1)\dots (x-x_{n-1})\\ & +f[x_0,x_1,\dots ,x_n]{\omega }_{n+1}(x)\\ =& N_n(x)+R_n(x)\end{array}$$

其中，

$$\begin{array}{rl}{N}_n(x)=& f(x_0)+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)+\\ & \dots +f[x_0,x_1,\dots ,x_n](x-x_0)(x-x_1)\dots (x-x_{n-1})\\ R_n(x)=& f[x_0,x_1,\dots ,x_n]{\omega }_{n+1}(x)\end{array}$$

其中，${\omega }_{n+1}(x)=(x-x_0)(x-x_1)\dots (x-x_n)$，$N_n(x)$就是大名鼎鼎的牛顿插值公式，其是一种十分强大的插值算法，递推式可以写为

$$N_{n+1}(x)=N_n(x)+f[x_0,x_1,\dots ,x_{n+1}]{\omega }_{n+1}(x)$$

由于牛顿插值的本质是多项式插值，所以关键是得到插值多项式的系数。记$N_{n,i}$为$n$阶牛顿多项式的第$i$项，记${\omega }_{n,i}$为$n$阶$\omega$多项式的第$i$项，则其递推式可以写为

$$N_n(x)=\sum _{i=0}^n{N}_{n,i}{x}^i=\sum _{i=0}^{n-1}{N}_{n-1,i}{x}^i+f[x_0,x_1,\dots ,x_n]\sum _{i=0}^n{\omega }_{n,i}{x}^i$$

则

$$\sum _{i=0}^n{N}_{n,i}{x}^i=\sum _{i=0}^{n-1}(N_{n-1,i}+f[x_0,x_1,\dots ,x_n]{\omega }_{n,i})x^i+f[x_0,x_1,\dots ,x_n]{\omega }_{n,n}{x}^n$$

拆分之后得到

$$N_{n,i}=\{\begin{array}{rlr}& N_{n-1,i}+f[x_0,x_1,\dots ,x_n]{\omega }_{n,i},& i<n\\ & f[x_0,x_1,\dots ,x_n]{\omega }_{n,n},& i=n\end{array}$$

由于${\omega }_n(x)=(x-x_0)(x-x_1)\dots (x-x_{n-1})={\omega }_{n-1}(x)\ast (x-x_n)$，则

$${\omega }_{n,i}=\{\begin{array}{rlr}& {\omega }_{n-1,0}\ast (-x_{{}_n})& i=0\\ & {\omega }_{n-1,i}\ast (-x_{{}_n})+{\omega }_{n-1,i-1}& i\in [1,n]\\ & 1& i=n+1\end{array}$$

polyMulti<-function(x){
    n = length(x)
    if(n<2) return(c(-x,1))
    omega = rep(0,n+1)
    omega[1] = - x[1]
    omega[2] = 1
    for(i in 2:n){
        omega[2:i] = -x[i]*omega[2:i]*+omega[1:(i-1)]
        omega[1] = -x[i]*omega[1]
        omega[i+1] = 1
    }
    return(omega)
}

Newton<-function(x,y){
    n = length(x)
    N = rep(0,n+1)
    N[1]=y[1]
    for(i in 1:n){
        omega = polyMulti(x[1:i])
        d = kDiffDiv(x[1:i],y[1:i],i-1)
        N[1:i] = N[1:i] + d*omega[1:i]
        N[i+1] = d*omega[i+1]
    }
    return(N)
}

验证一下

x = sort(rnorm(10))
y = x^5+2*x^4
N = Newton(x,y)
Y = y*0
for(i in 1:length(Y))
    for(j in 1:length(N))
        Y[i] = Y[i]+N[j]*x[i]^(j-1)
plot(x,y)
lines(x,Y)

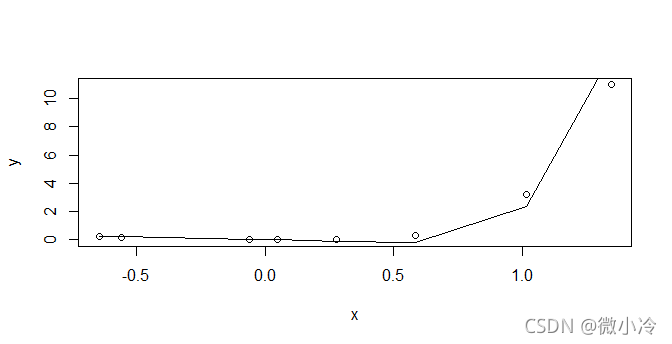
可见效果还是不错的。