目录
问题描述:
实现代码与解析:
通用写法(递归):
原理思路:
依据二叉搜索树特性写法(递归):
原理思路:
迭代:
原理思路:
问题描述:
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
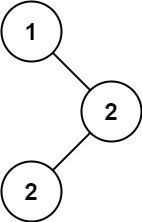
输入:root = [1,null,2,2] 输出:[2]
示例 2:
输入:root = [0] 输出:[0]
实现代码与解析:
通用写法(递归):
class Solution {
public:
//遍历
void traversal(TreeNode* cur,unordered_map<int,int>& map)
{
if(cur==NULL) return;
map[cur->val]++;//对应值的频率加一
traversal(cur->left,map);
traversal(cur->right,map);
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b)
{
return a.second > b.second;
}
vector<int> findMode(TreeNode* root)
{
unordered_map<int,int> map;//<结点值,频率>
vector<int> result;//结果
traversal(root,map);
vector<pair<int,int>> vec(map.begin(),map.end());
sort(vec.begin(),vec.end(),cmp);//根据频率排序一下
result.push_back(vec[0].first);
for(int i=1;i<vec.size();i++)
{
if(vec[i].second==vec[0].second)
{
result.push_back(vec[i].first);
}
else
{
break;
}
}
return result;
}
};原理思路:
二叉树求众数的通用写法,非二叉搜索树也可以用。
1、首先用map<结点值,频率>来接收遍历结果,
2、然后再依据频率排序,由于map只能依据key来排序,不能依据value,所以我们这里先转化成vector<pair<int,int>>来进行排序。
3、最后取出频率最大的一个值或多个值,放入result数组中。
下面介绍二叉搜索树的写法,当然二叉搜索树也可以用上面这种通用写法。
依据二叉搜索树特性写法(递归):
class Solution {
public:
TreeNode* pre=NULL;//记录前一个结点
int maxCount=0;//最大频率
int count=0;//统计频率
vector<int> vec;//记录众数,可能有多个,我们用数组记录
void traversal(TreeNode* cur)
{
if(cur==NULL) return;
traversal(cur->left);//左
//第一个结点
if(pre==NULL)
{
count=1;//更新当前频率
}
//若与前一结点值相同
else if(pre->val==cur->val)
{
count++;
}
//与前一个结点值不同
else
{
count=1;
}
//若当前频率等于最大频率
if(count==maxCount)
{
vec.push_back(cur->val);//记录该结点值
}
//若当前频率大于最大频率
else if(count>maxCount)
{
maxCount=count;//更新最大值
vec.clear();//最大频率已经改变,凭空之前的记录值
vec.push_back(cur->val);
}
pre=cur;//跟新前一结点
traversal(cur->right);//右
}
vector<int> findMode(TreeNode* root)
{
traversal(root);
return vec;
}
};原理思路:
和二叉搜索树一样,我们肯定还是在中序处理结点。
1、首先我们要定义maxCount来记录最大频率,count来记录当前遍历结点值的频率,在过程中要不断更新,还要定义一个pre来记录前一个结点值,以及result数组来记录结果。
2、中序处理:首先要获取当前count值,若pre为空,说明是第一个结点,直接令count=1即可。
3、若pre不空,判断pre的值与当前结点值是否相等,若相等,count++,若不相等,依旧令count=1,我们就得到了当前count值。
4、然后我们就要用count和maxCount做比较,若相等,说明此元素为当前遍历过的结点中的最大频率相同的众数,result记录其值,若count大于maxCount,说明此元素的频率超过了最大频率,我们清空result,将新的最大频率的值放入result数组中,清空result是容易忽略的点,大家要注意一下,result一定要清空,因为此时最大频率已经变了,之前记录的结果显然需要去除掉。
5、最后别忘了,更新pre,记录结点,作为下一个结点的前一个结点。
其实注释写的已经很具体了,大家可以结合注释看。
迭代:
class Solution {
public:
vector<int> findMode(TreeNode* root)
{
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
int maxCount = 0; // 最大频率
int count = 0; // 当前频率
vector<int> result;
while (cur != NULL || !st.empty()) {
if (cur != NULL)
{
st.push(cur);
cur = cur->left;
}
else
{
cur = st.top();
st.pop();
// 第一个节点
if (pre == NULL)
{
count = 1;
}
// 与前一个节点数值相同
else if (pre->val == cur->val)
{
count++;
}
// 与前一个节点数值不同
else
{
count = 1;
}
if (count == maxCount)
{
result.push_back(cur->val);
}
if (count > maxCount)
{
maxCount = count; // 更新最大频率
result.clear(); // 清空result
result.push_back(cur->val);
}
pre = cur;
cur = cur->right;
}
}
return result;
}
};原理思路:
中序迭代遍历,没什么可说的,和递归原理相同。