本次内容参考自高等教育本科教材《实验设计与数据处理》

一、正交实验基础知识介绍

1.1 认识正交表

先看一组正交表的构造

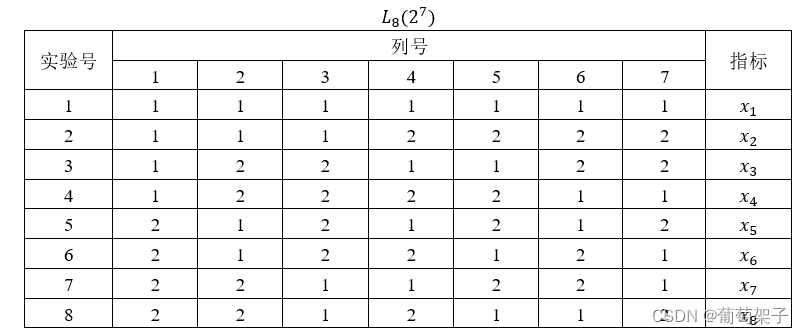
这个表的题头代表了这个表的构造，其中L代表了正交表，8是行数，底数2是水平数，指数7代表了列数与因素的数量。

1.2 正交表的特点

正交表是一种特殊的实验设计表，其根据正交性原则构造，常用于多因素实验设计。正交表的特点包括：

1. 实验次数大幅减少：正交实验设计方法通过选取部分有代表性的点进行实验，能够在较少的实验次数下，评价多个因素如何影响实验结果。

2. 均衡性和比较性：正交表设计的每一个因素在实验中的水平出现次数相同，确保了实验的均衡性。不同水平组合的实验次数相同，这使得水平间的比较具有公平性。

3. 整齐性和可重复性：正交实验设计的表格格式整齐，便于操作和分析数据。此外，实验的设计是可重复的，即其他研究者可以采用相同的设计方法来重复实验（这里只是突出广泛性）。注意实验者不用重复实验。

4. 正交性：正交表中任意两列均满足正交性，即在表中任意两个因素的任意水平组合出现的次数都相同。这种设计确保了因素之间的独立性，使得在分析结果时可以单独考虑每个因素的效果。

5. 容错性：尽管实验次数减少，但正交表设计的容错性较高，即使部分实验数据丢失或有误，也不会对实验结果的整体趋势和结论产生重大影响。

6. 灵活性和可扩展性：根据实验需要，可以选择不同大小和层次的正交表，并且可以通过合并实验水平扩展正交表的规模。

7. 易于实验结果分析：因为正交表设计的结构化，使用方差分析（ANOVA）等统计方法可以更方便地分析数据，识别哪些因素对结果有显著影响。

正交表的这些特点使其在工程、农业、质量管理等多个领域中被广泛应用，尤其是在产品设计和工艺优化中，正交试验设计可以有效地帮助研究人员在众多因素和水平中找到最佳的组合。

1.3 正交表的分类

正交表的分类主要基于因素的数量和每个因素的水平数量来划分。两个最重要的参数是：

1. 因素数（或列数）：正交表中可以包含的因素（也称为参数或变量）的数量。
2. 水平数：每个因素可以取的不同值的数量。

基于这些参数，正交表可以分为以下几类：

1. 标准正交表（Standard Orthogonal Tables）：

   • 这些表通常用记号 L_n(s^k) 表示，其中：
     • L 表示表是正交的（Latin square的缩写）。
     • n 表示实验的总次数（或行数）。
     • s 表示每个因素的水平数。
     • k 表示因素的个数。
   • 例如，L₉(3⁴) 表示一个每个因素有3个水平，总共有4个因素，需要进行9次实验的正交表。

2. 混合水平正交表（Mixed-Level Orthogonal Tables）：

   • 当我们的实验设计中含有不同水平数的因素时，就会使用混合水平正交表。
   • 符号例如 L₁₈(2¹3⁷) 表示有一个因素有2个水平，七个因素每个有3个水平，总共需要进行18次实验。

3. 复合正交表（Composite Orthogonal Tables）：

   • 当一个实验设计中的某些因素需要更多的水平数，或者需要考虑更多的交互作用时，可以通过组合两个或更多的标准正交表来构造复合正交表。

正交表的具体展现通常是一个矩阵，其中每一行代表一次实验的设置，每一列代表一个因素，表中的数字表示因素的水平。例如，一个 L₈(2⁷) 正交表可以如下所示：

二、数据分析

我们以一个实际例子来说明：
化工厂为了提高产品的收率，用正交表安排实验，其加工条件如下：
因素A 反映温度：A₁ =30^° C, A₁ =40^°

因素B 反应时间：B₁=60min, B₂=90min

因素C 原料配比: C₁=1:1, C₂=1.5:1

因素D 搅拌速度: D₁=慢, D₂=快

1.首先我们应该明确实验的目的，比如说这个例子的目的在于提高产品生产率，那么可以用产品的收率（%）来表征；

2.第二步我们需要选取实验的因素与水平，这个也是最为关键的一步，对于因素及水平少的就直接选取就行，比如这个简单的例子，但是很多实验并无法直接得到，比如齿轮机械加工过程中参数的选取，就要结合经验确定一个大致的范围，或者进行一些探索性实验来确定实验精度，另外一些更加复杂的可能就要进行序贯实验等；

3.选用正交表/表头设计 ，简单实验就选取标准的正交表，复杂可能需要采用混合表等，需要单独设计表头，需要注意的是，对于温度影响较大的实验，应该选择一些尽量小的表，这个例子有四个因素，2个水平，因此选用
L₈(2⁷)
但是这个有7列，，这里一般第3，5，6列来安排交互作用，
在实验设计中，交互作用指的是两个或多个因素同时影响实验结果的情况，这种影响并不是各自独立因素影响的简单叠加。换句话说，当两个（或多个）因素同时变化时，它们对实验结果的联合效应与它们各自效应的总和不同。
举例来说，假设我们正在研究一种化学药品的效果，这种效果可能会受到温度和pH值的影响。如果温度的变化对药品效果有一定的影响，pH值的变化也有一定的影响，那么这两者的交互作用可能意味着当同时改变温度和pH值时，药品效果的变化并非温度影响和pH影响的简单相加，而是可能会有更加复杂的效果出现。例如，高温可能会加强或减弱不同pH值下药品的效果。
因此这里把四个因素分别置于第1、第2、第4和第7列。

4.按正交表进行实验，可以不按表里的顺序进行，但一定要全部做完才能开始进行数据分析。

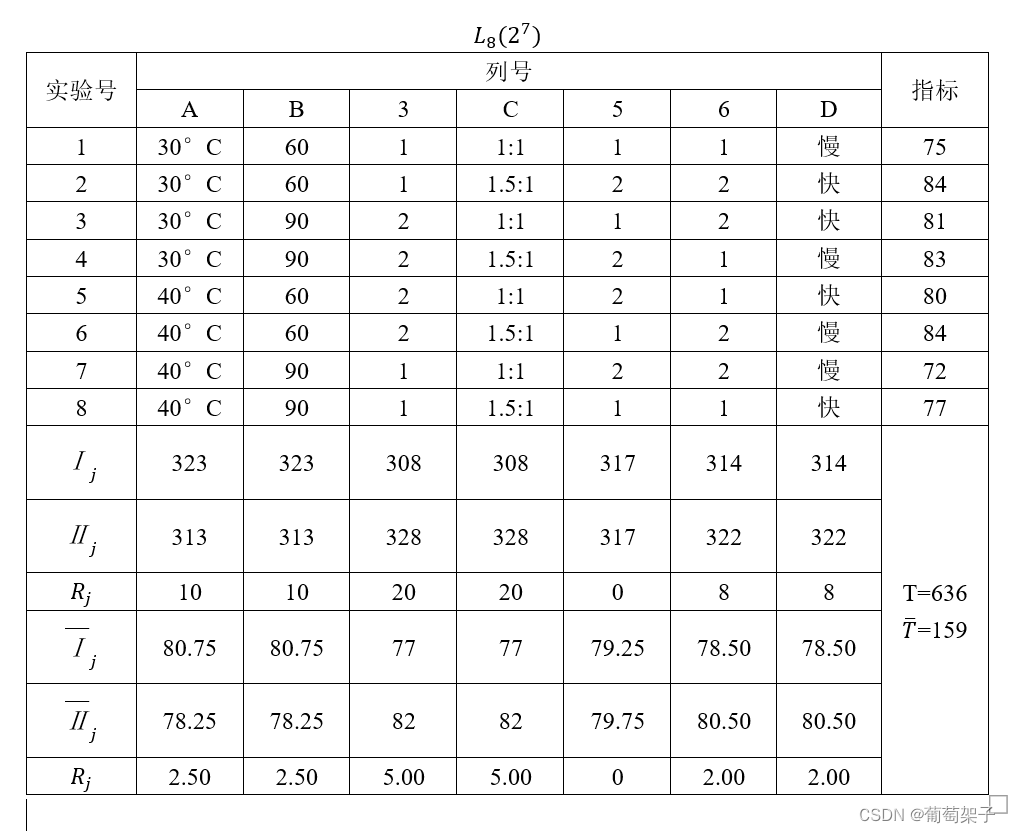
接下来我们分析这个表中的数据，那么通过分析数据我们能够得到什么信息呢：
1.哪些因素对指标影响大，哪些因素影响小或者没有影响
2.选择出对指标最优的因素水平
Ⅰ_j代表了不同水平下的和数，比如Ⅰ₁就是第一列第一水平对应指标的和数，即

Ⅰ₁=75+84+81+83=323
同理Ⅱ₁就是第一列第二水平对应指标的和数，即
Ⅱ₁=80+84+72+77=313

R_j是不同列下指标的极差（最大值-最小值），

R₁=323-313=10
而这些，就是平均值，

比如说323/4=80.75等，
T是所有试验结果（就是指标的叠加）的和，
T=75+84+81+83+80+84+72+77=636
接下来我们来分析，首先看数据，其中第2和6组试验结果最好，但是并没有具体的信息，我们继续往下看，首先看Ⅰ₁和Ⅱ₁
拿A看，Ⅰ₁>Ⅱ₁,所以A应该取1水平，同理B应该取1水平。C取2水平，D取2水平；

然后我们对因素影响力大小进行分析，这个看极差，可以看出，C的极差是5.00，最大，因此影响力排序：C>A=B>D;

到这里结束了，但是当然不会这么简单，比如我们得到的只是数据里面的最优解，但是实际呢，我们要不要继续往下实验呢，中间的空列比如说第三列，属于交互列，这里没考虑，如果加入的话，就会有所不同了；
后续会慢慢增加这部分知识。