2010年认证杯SPSSPRO杯数学建模
A题 聪明的汽车
原题再现:
在狭窄的空间里把车停放在合适的位置,或在短小的停车位上侧位停车,一直是考验驾驶员技术与信心的问题。有调查报告称:57% 的驾驶员对自己的停车技术缺乏自信,这一方面影响人的驾驶体验,一方面也使停车空间不能得到充分利用。在此,请你协助驾驶员来解决停车的问题。具体要求如下:
第一阶段问题:
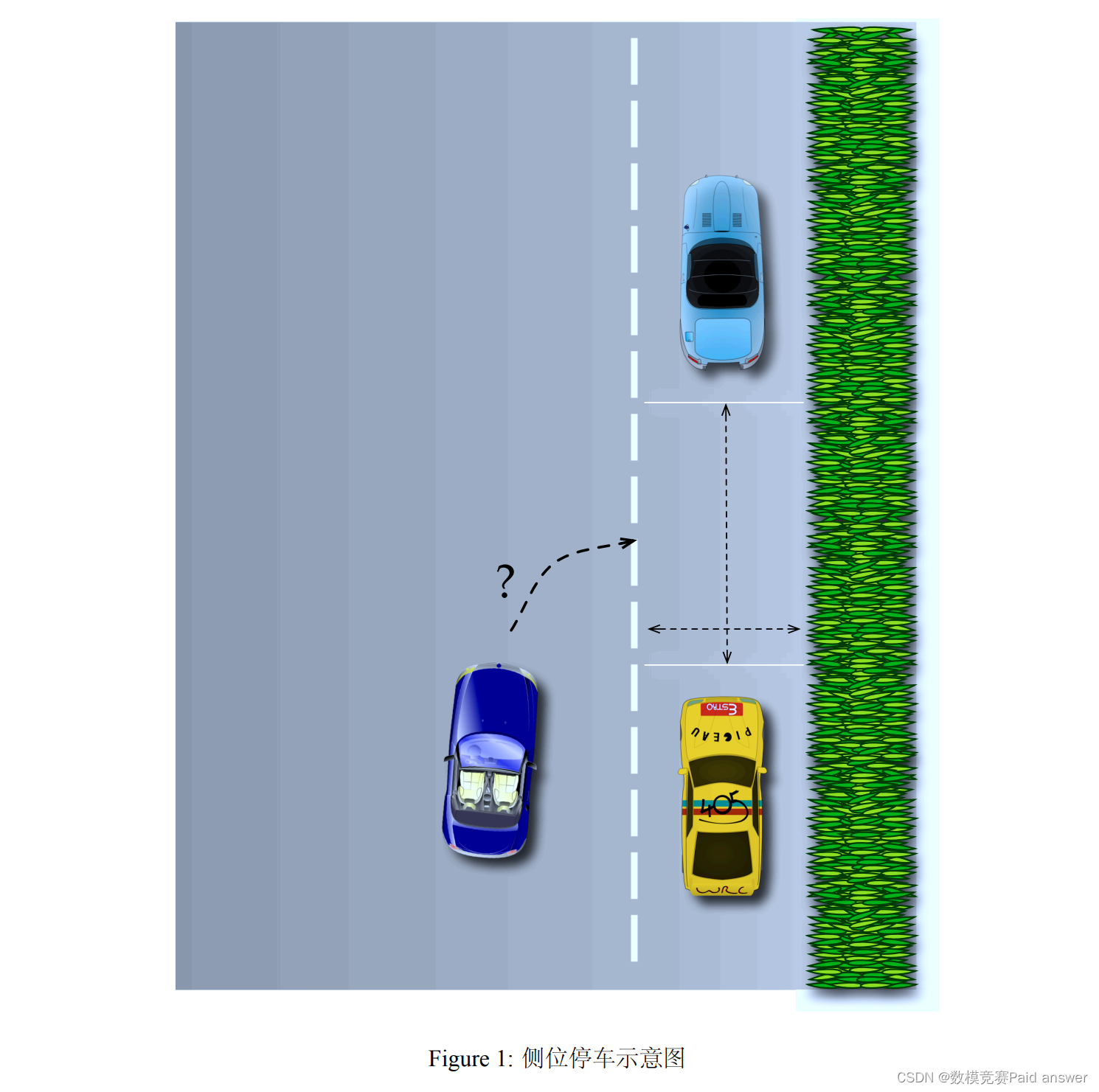
(1) 对侧位停车而言,在空位较短的时候,驾驶员会难以确定自己的汽车是否能顺利停入。请你建立合理的模型,以判断本车是否能在该处侧位停车。我们假设可以得到停车位置的平面图1,包括停车空位的长度宽度等数据。考虑到实用性,模型所需的本车数据要能够容易测得,例如几何尺寸、转弯半径等。
(2) 我们假设停车位置的平面图能够显示在汽车的车载显示器上。请给出本车为了进入停车位,应当从哪个位置和角度进入。将理想线路以及允许的偏差显示在图上。
整体求解过程概述(摘要)
” 聪明的汽车” 是一个关于汽车能否以及怎样安全泊进停车区域的问题。为了解决这个问题,首先,我们对安全泊车进行了定义,在这样的前提下,建立了模型一,只考虑两次泊车即可完成的情形,运用逆向思维,考虑汽车从停车位倒车驶出或开车前进驶出这两种情况,在具体的模型求解中,我们对这两种情况作了具体的理论性的阐述,并求出了最优解,得到了极限停车区域以及最大的安全泊车区域,那么,在安全区域中行驶的车便可以安全泊车,反之则不能安全泊车。在这个模型下我们得到了车位的长和宽,分别为7.8453m,2.0570m 这与真实值相当接近。我们进一步进行了人性化,给了司机、车辆、天气一定的宽松条件,模型与实际也就比较吻和了;然而,模型一还是有其局限性,主要体现在它只考虑了二次泊车成功的情况,这样就很大程度上限制了车的行进,在某种程度上延长了最小的停车区域,在这样的情形下,我们考虑建立模型二,以达到优化模型一以及更加人性化的目的。为了更好地说明问题,我们先从经过三次泊车做起,在这样的前提下,同样运用了最小转弯半径这一汽车的重要参数值,考虑汽车进行第一次泊车时汽车已经以最小转弯半径行驶,并确定出其最佳的泊车位置,在这里我们也充分利用了”紧约束” 这一极限条件,使得停车区域能够达到最小,经过此番考虑后,我们可以进行多次泊车以达到最终目的,其算法与三次泊车基本相同,也就不用再赘述了。综上可知,两个模型都采用了” 紧约束” 这样的假设,以达到我们所需要的目的,求出了最佳的泊车路线,解决了上题目中所阐述的两个问题。
问题分析
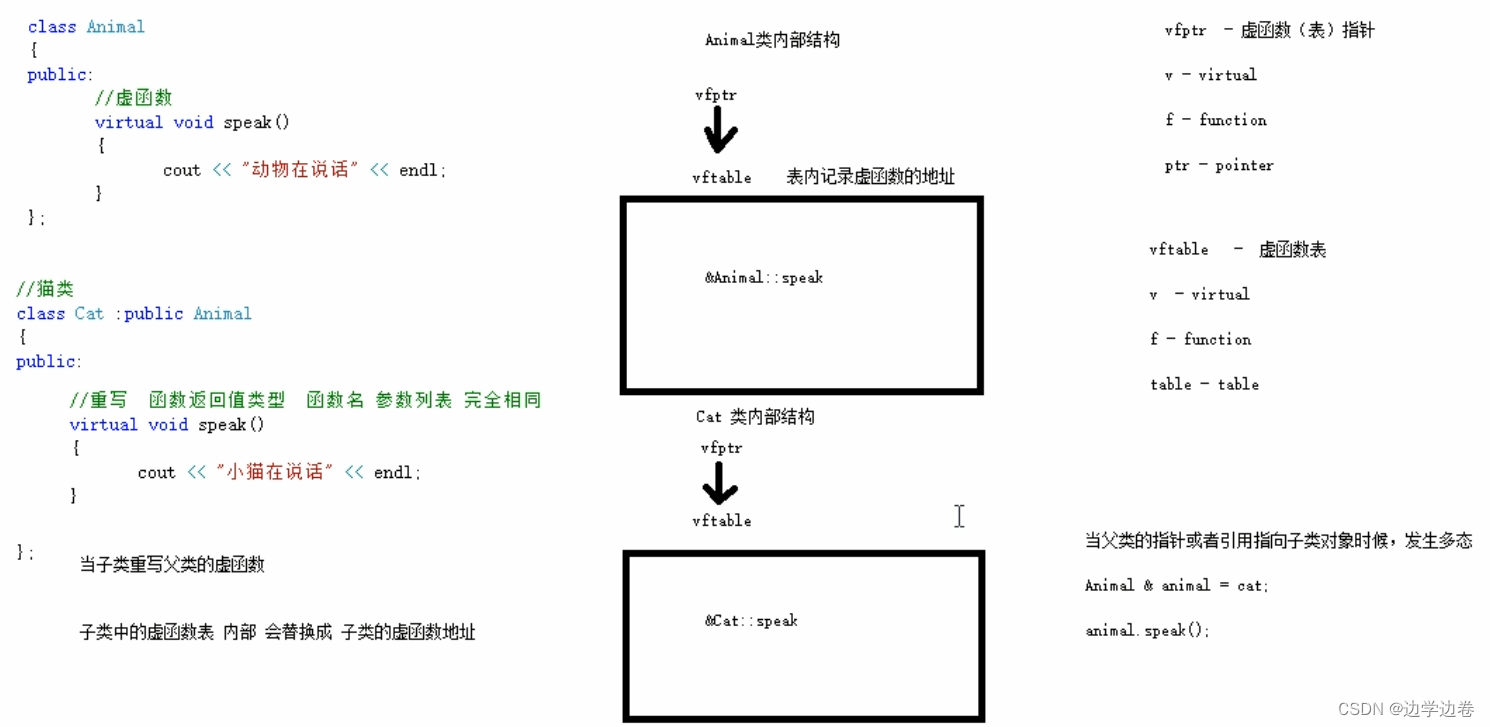
分析车辆平行泊车的全过程,有两个因素对平行泊车质量影响较大,一为汽车动力学特性,二为环境因素。汽车的动力学特性即车辆自身参数,包括车长、车宽、前悬、最小转弯半径;环境因素主要是道路参数,包括停车位长度、停车位宽度、泊车初始位置,即泊车时两平行车辆间水平距离。泊车过程有影响的几个重要参数,结合下图进行下说明:
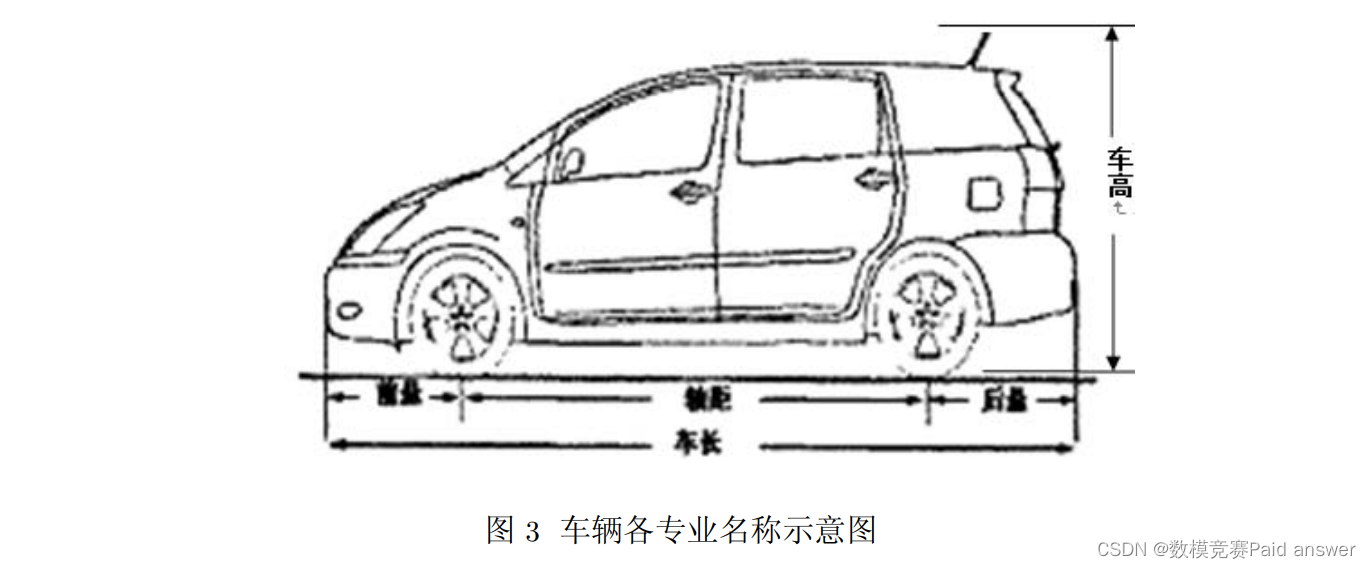
1. 车过程有影响的几个重要参数:
2. 车宽 (vehicle width):汽车最左端到最右端的距离,不包括反光镜、转向侧灯、脚踏板等部位。
3. 轴距 (wheel base):汽车前轴中心至后轴中心的距离。
4. 前悬 (front overhang):汽车最前端至前轴中心的距离。汽车的基本参数中不包括前悬,可通过车长与轴距计算前悬的长度。
5. 最小转弯半径 (minimum turning radius):转向盘转到极限位置时的转弯半径为最小转弯半径。当转向盘转到极限位置,汽车以最低稳定车速转向行驶时,外侧转向轮的中心平面在支承平面上滚过的轨迹园半径。它很大程度上表征了汽车能够通过狭窄弯曲地带或绕过不礓越过的障碍物的能力。转弯半径越小,汽车的机动性能越好。图 4中所示 d,为汽车的最小转弯半径。
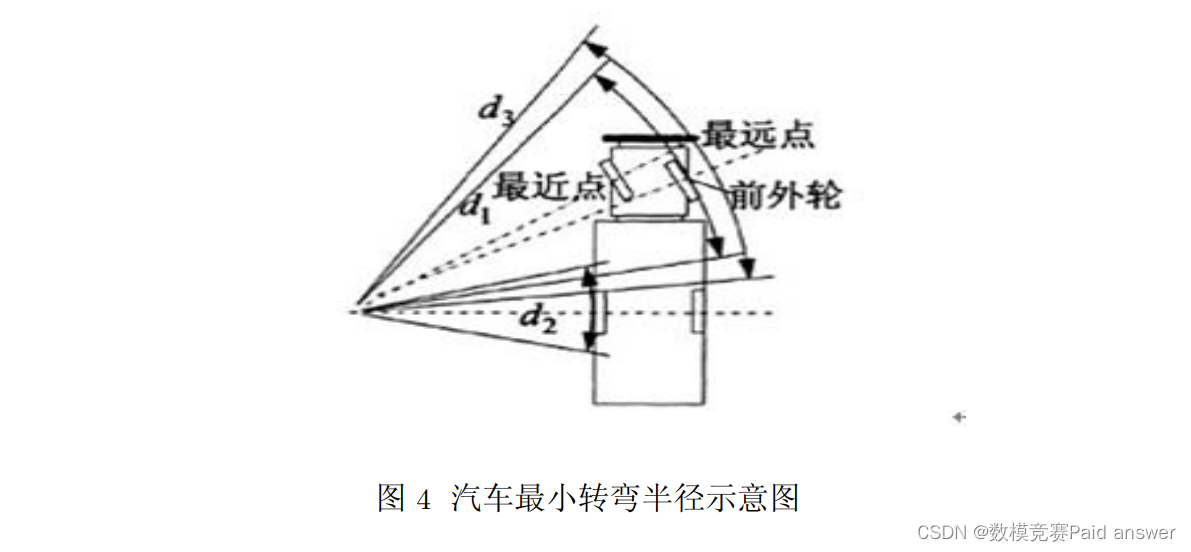
6. 车位长度 (1ength of parking space):路旁停车位前后都停有车辆时,前方车辆尾部到后方车辆头部的距离。
7. 车高:(vehicle height) 至地面间的距离。
8. 轮距:(vehicle tread) 同一车轿左右轮胎中心线间的距离。
对于问题一,假设我们可以得到停车位置的平面图,包括停车空位的长度宽度等数据,需要建立合理的模型,以判断本车是否能在该处测位停车, 我们从最小半径入手,考虑两次泊车的情况,可以求得最小的停车区域,从而也就可以获得最大的安全区域,如果汽车在处于安全区域中,则显然可以安全泊车,反之,则不能安全泊车。从这个方向入手,考虑定义的车的各个半径与边界可能碰撞的临界值,从而确立了一个大致的安全区域,也就建立了约束条件,从而可以得到一个最小停车位的最小长度和宽度,与已知的相比较即可给驾驶员提供一个参考数据,判断自己是否是一个“聪明的汽车”。接下来从人性化的角度考虑,上述情况没有考虑到汽车速度对于泊车停车位的影响,我们引入司机一般的转向时间的考虑,得出更加合理化的最小停车位的范围。在泊车过程中一次往往是不能达到满意的泊车,从而我们提出多次泊车达到理想泊车的情况建立受各边界点反复约束非线性方程组,从而可以求出更加精确的停车位约束值。
对于问题二,在问题一的基础上进行优化,进一步得到需要的结果。
模型的假设:
1. 汽车泊车过程中无侧滑现象产生
2. 车辆前轮的运行精确到控制下的理想路径
3. 计算汽车宽度时不考虑反光镜,转向侧灯,脚踏板等
4. 路面及周围环境对汽车运行状况无影响
5. 我们在各大正规网站上查到的数据均真实有效
论文缩略图:

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
sets: l1=SQRT(d12 + d0
2 + 2 ∗ d1 ∗ d0 − d
2 + 2 ∗ d ∗ d0 ∗ COT(t)) + d1 + d0;
l2=SQRT((d02 − d
2 + 2 ∗ (d0/SIN(t)) ∗ d ∗ COS(t) + d1 + d0; M ax = l1 − l2;
d12 + d0
2 + 2d1 ∗ d0 − d
2 + 2d ∗ d0 ∗ COT(t) > 0;
sqrt((d02 − d
2 + 2d0/SIN(t)dCOS(t)) + d1 + d0 > 0;
@bnd(3.14/6,t,3.14/4);
@bnd(2,d,2.8);
@bnd(2,d0,3);
@bnd(0.8,d1,1.5);
@bnd(1,d2,1.5);
end;