数据结构

数组 & 链表
相连性 | 指向性
数组可以迅速定位到数组中某一个节点的位置
链表则需要通过前一个元素指向下一个元素，需要前后依赖顺序查找，效率较低

实现链表

//    head => node1 => node2 => ... => null

class Node {
    constructor(element) {
        this.element = element;
        this.next = null;
    }
}


class LinkList {
    constructor() {
        this.length = 0;
        //    1.空链表特征 => 判断链表的长度
        this.head = null;
    }
    
    //    返回索引对应的元素
    getElementAt(position) {
        //    边缘检测
        if (position < 0 || position >= this.length) {
            return null;
        }
        
        let _current = this.head;
        for (let i = 0; i < position; i++) {
            _current = _current.next;
        }
        
        return _current;
    }
    
    //    查找元素所在位置
    indexOf(element) {
        let _current = this.head;
        for (let i = 0; i < this.length; i++) {
            if (_current === element) return i;
            _current = _current.next;
        }
        return -1;
    }
    
    //    添加节点 在尾部加入
    append(element) {
        _node = new Node(element);
        
        if (this.head === null) {
            this.head = _node;
        } else {
            this.getElementAt(this.length - 1);
            _current.next = _node;
        }
        this.length++;   
    }
    
    //    插入节点    在中间插入
    insert(position, element) {
        if (position < 0 || position > this.length) return false;
        
        let _node = new Node(element);
        if (position === 0) {
            _node.next = this.head;
            this.head = _node;
        } else {
            let _previos = this.getElementAt(position - 1);
            _node.next = _previos;
            _previos.next = _node;
        }
        this.length++;
        return true;
    }
    
    //    删除指定位置元素
    removeAt(position) {
        if (position < 0 || position > this.length) return false;
        
        if (position === 0) {
            this.head = this.head.next;
        } else {
            _previos = this.getElementAt(position - 1);
            let _current = _previos.next;
            _previos.next = current.next;            
        }
        this.length--;
        return true;
    }
    
    //    删除指定元素
    remove(element) {
    }
}

栈

特点：先入后出（薯片桶）

队列

特点：先入先出（排队）

哈希

特点：快速匹配定位

树

遍历 前序遍历（中左右） 中序遍历（左中右） 后序遍历（左右中）
1.二叉树 or 多子树
2.结构定义
a.树是非线性结构
b.每个节点都有0个或多个后代

面试真题：

判断括号是否有效自闭合

算法流程：
1.确定需要什么样的数据结构，满足模型的数据 - 构造变量 & 常量
2.运行方式 简单条件执行 | 遍历 | 递归 - 算法主体结构
3.确定输入输出 - 确定流程

    //    '{}[]' 和 '[{}]' true,   
    //    '{{}[]' false
const stack = [];

const brocketMap = {
    '{': '}',
    '[': ']',
    '(': ')'
};

let str = '{}';

function isClose(str) {
    for (let i = 0; i < str.length; i++) {
        const it = str[i];
        if (!stack.length) {
            stack.push(it);
        } else {
            const last = stack.at(-1);
            if (it === brocketMap[last]) {
                stack.pop();
            } else {
                stack.push(it);
            }
        }
    }
    
    if (!stack.length) return true;

    return false;
}

isClose(str);

遍历二叉树

//    前序遍历
class Node {
    constructor(node) {
        this.left = node.left;
        this.right = node.right;
        this.value = node.value;
    }
}
//    前序遍历
const PreOrder = function(node) {
    if (node !== null) {
        console.log(node.value);
        PreOrder(node.left);
        PreOrder(node.right);
    }
}
//    中序遍历
const InOrder = function(node) {
    if (node !== null) {
        InOrder(node.left);
        console.log(node.value);
        InOrder(node.right);
    }
}
//    后序遍历
const PostOrder = function(node) {
    if (node !== null) {
        PostOrder(node.left);
        PostOrder(node.right);
        console.log(node.value);
    }
}

树结构深度遍历

const tree = {
    value: 1,
    children: [
        {
            value: 2,
            children: [
                { value: 3 },
                {
                    value: 4, children: [
                        { value: 5 }
                    ]
                }
            ]
        },
        { value: 5 },
        {
            value: 6, 
            children: [
                { value: 7 }
            ]
        }
    ]
}
//    优先遍历节点的子节点 => 兄弟节点
//    递归方式
function dfs(node) {
    console.log(node.value);
    if (node.children) {
        node.children.forEach(child => {
            dfs(child);
        })   
    }
}

//    遍历 - 栈
function dfs() {
    const stack = [node];
    while (stack.length > 0) {
        const current = stack.pop();
        console.log(current.value);
        if (current.children) {
            const list = current.children.reverse();
            stack.push(...list);
        }
    }
 }

树结构广度优先遍历

const tree = {
    value: 1,
    children: [
        {
            value: 2,
            children: [
                { value: 3 },
                {
                    value: 4, children: [
                        { value: 5 }
                    ]
                }
            ]
        },
        { value: 5 },
        {
            value: 6, 
            children: [
                { value: 7 }
            ]
        }
    ]
}

//    1. 递归
function bfs(nodes) {
    const list = []
    nodes.forEach(child => {
        console.log(child.value);
        if (child.children && child.children.length) {
            list.push(...child.children);
        }
    })
    if (list.length) {
        bfs(list);    
    }
}
bfs([tree]);

//    1.递归 - 方法2
function bfs(node, queue = [node]) {
    if (!queue.length) return;
    
    const current = queue.shift();
    if (current.children) {
        queue.push(...current.children);
    }
    
    bfs(null, queue);
}
bfs(tree);


//    2. 递归
function bfs(node) {
    const queue = [node];
    while(queue.length > 0) {
        const current = queue.shift();
        if (current.children) {
            queue.push(...current.children);
        }
    }
}

实现快速构造一个二叉树

1.若他的左子树非空，那么他的所有左子节点的值应该小于根节点的值
2.若他的右子树非空，那么他的所有右子节点的值应该大于根节点的值
3.他的左 / 右子树 各自又是一颗满足下面两个条件的二叉树

class Node {
    constructor(key) {
        this.key = key
        this.left = null;
        this.right = null;
    }
}

class BinaryTree {
    constructor() {
    //    根节点
        this.root = null;
    }
    
    //    新增节点
    insert(key) {
        const newNode = new Node(key);
        
        const insertNode = (node, newNode) => {
            if (newNode.key < node.key) {
    //    没有左节点的场景 => 成为左节点
                node.left ||= newNode;
                
    //    已有左节点的场景 => 递归改变参照物，与左节点进行对比判断插入位置
                inertNode(node.left, newNode);
            } else {
    //    没有左节点的场景 => 成为左节点
                node.right ||= newNode;
                
    //    已有左节点的场景 => 递归改变参照物，与左节点进行对比判断插入位置
                inertNode(node.right, newNode);
            }
        }
        
        this.root ||= newNode;
        //    有参照物后进去插入节点
        insertNode(this.root, newNode);
    }
    
    //    查找节点
    contains(node) {        
        const searchNode = (referNode, currentNode) => {
            if (currentNode.key === referNode.key) {
                return true;
            }
            if (currentNode.key > referNode.key) {
                 return searchNode(referNode.right, currentNode);
            }
            
            if (currentNode.key < referNode.key) {
                 return searchNode(referNode.left, currentNode);
            }
            
            return false;
        }
        return searchNode(this.root, node);
    }
    
    //    查找最大值
    findMax() {
        let max = null;
        
        //    深度优先遍历
        const dfs = node => {
            if (node === null) return;
            if (max === null || node.key > max) {
                max = node.key;
            }
            dfs(node.left);
            dfs(node.right);
        }
        
        dfs(this.root);
        return max;
    }
    
    //    查找最小值
    findMin() {
        let min = null;
        
        //    深度优先遍历
        const dfs = node => {
            if (node === null) return;
            if (min === null || node.key < min) {
                min = node.key;
            }
            dfs(node.left);
            dfs(node.right);
        }
        
        dfs(this.root);
        return min;
    }
    
    //    删除节点
    remove(node) {
        const removeNode = (referNode, current) => {
            if (referNode.key === current.key) {
                if (!node.left && !node.right) return null;
                if (!node.left) return node.right;
                if (!node.right) return node.left;
                
            }
        }
        
        return removeNode(this.root, node);
    }
}

平衡二叉树

class Node {
    constructor(key) {
        this.key = key;
        this.left = null;
        this.right = null;
        this.height = 1;
    }
}


class AVL {
    constructor() {
        this.root = null;
    }
    
    // 插入节点
    insert(key, node = this.root) {
    	if (node === null) {
    		this.root = new Node(key);
    		return;
    	}
    
    	if (key < node.key) {
    		node.left = this.insert(key, node.left);
    	} else if (key > node.key) {
    		node.right = this.insert(key, node.right);
    	} else {
    		return;
    	}
    
    	// 平衡调整
    	const balanceFactor = this.getBalanceFactor(node);
    	if (balanceFactor > 1) {
    		if (key < node.left.key) {
    			node = this.rotateRight(node);
    		} else {
    			node.left = this.rotateLeft(node.left);
    			node = this.rotateRight(node);
    		}
    	} else if (balanceFactor < -1) {
    		if (key > node.right.key) {
    			node = this.rotateLeft(node);
    		} else {
    			node.right = this.rotateRight(node.right);
    			node = this.rotateLeft(node);
    		}
    	}
    
    	this.updateHeight(node);
    	return node;
    }
    
    // 获取节点平衡因子
    getBalanceFactor(node) {
        return this.getHeight(node.left) - this.getHeight(node.right);
    }
    
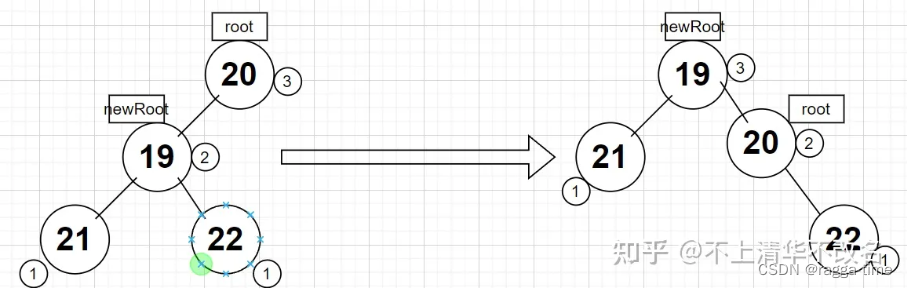
    rotateLeft(node) {      
        const newRoot = node.right;        
        node.right = newRoot.left;        
        newRoot.left = node;
        
        //    这里是为了校准更新的这两个节点的高度。只需要把他的左右节点的高度拿来 加1即可
        node.height = Math.max(
            this.getHeight(node.left),
            this.getHeight(node.right)
        ) + 1;
        newRoot.height = Math.max(
            this.getHeight(newRoot.left),
            this.getHeight(newRoot.right)
        ) + 1;

        return newRoot;
    }
    
    getHeight(node) {
        if (!node) return 0;
        return node.height;
    }
}

红黑树

参考写法

let RedBlackTree = (function() {
    let Colors = {
        RED: 0,
        BLACK: 1
    };

    class Node {
        constructor(key, color) {
            this.key = key;
            this.left = null;
            this.right = null;
            this.color = color;

            this.flipColor = function() {
                if(this.color === Colors.RED) {
                    this.color = Colors.BLACK;
                } else {
                    this.color = Colors.RED;
                }
            };
        }
    }

    class RedBlackTree {
        constructor() {
            this.root = null;
        }

        getRoot() {
            return this.root;
        }

        isRed(node) {
            if(!node) {
                return false;
            }
            return node.color === Colors.RED;
        }

        flipColors(node) {
            node.left.flipColor();
            node.right.flipColor();
        }

        rotateLeft(node) {
            var temp = node.right;
            if(temp !== null) {
                node.right = temp.left;
                temp.left = node;
                temp.color = node.color;
                node.color = Colors.RED;
            }
            return temp;
        }

        rotateRight(node) {
            var temp = node.left;
            if(temp !== null) {
                node.left = temp.right;
                temp.right = node;
                temp.color = node.color;
                node.color = Colors.RED;
            }
            return temp;
        }

        insertNode(node, element) {

            if(node === null) {
                return new Node(element, Colors.RED);
            }

            var newRoot = node;

            if(element < node.key) {

                node.left = this.insertNode(node.left, element);

            } else if(element > node.key) {

                node.right =this.insertNode(node.right, element);

            } else {
                node.key = element;
            }

            if(this.isRed(node.right) && !this.isRed(node.left)) {
                newRoot = this.rotateLeft(node);
            }

            if(this.isRed(node.left) && this.isRed(node.left.left)) {
                newRoot = this.rotateRight(node);
            }
            if(this.isRed(node.left) && this.isRed(node.right)) {
                this.flipColors(node);
            }

            return newRoot;
        }

        insert(element) {
            this.root = insertNode(this.root, element);
            this.root.color = Colors.BLACK;
        }
    }
    return RedBlackTree;
})()