本次n皇后问题主要通过dfs(深度优先搜索)实现,加深对深度优先搜索的理解。
文章目录
前言
一、n皇后问题
二、算法思路
三、使用步骤
1.代码如下
2.读入数
3.代码运行结果
总结
前言
本次n皇后问题主要通过dfs(深度优先搜索)实现,加深对深度优先搜索的理解。
提示:以下是本篇文章正文内容,下面案例可供参考
一、n皇后问题
n皇后问题是指将n个皇后放到n*n的棋盘上面,皇后放置具有一定的规则,即每个皇后不能放在同一行,同一列,同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
每个解决方案占 n行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
数据范围
1≤n≤9
二、算法思路
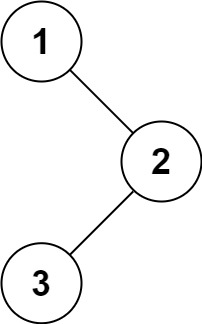
我们引入二维字符数组g来存储棋盘和皇后,皇后用字符‘Q’,表示,棋盘该空格上什么也没有用字符‘.’表示。分别引入一维布尔类型数组col、dg、udg,分别表示列、斜对角线、、反斜对角线。

图1.1 思路模拟
关于对角线我们可以通过截距来表示,即如果这些点都在同一个对角线线上,那么他们把横纵坐标代入算出来的截距b一定是相同的。反斜对角线的b = y+x;那么斜对角线b = y - x,又因为这个值可以为负的,我们加一个n来保证值不会变成负的,那么范围会变成(0,2n),所以我们的布尔类型数组要开2倍的n大小。(注:因为我们每行就放一个皇后,那么行就不需要开布尔类型数组判断)。
我们通过dfs来传入参数x表示每一行,当然递归的出口就是我们把每一行都处理完,当此时的x = n时(x从0到开始),我们把此时的棋盘打印即可。然后dfs内部再枚举每一列y,当col[y] = dg[y-x+n] = udg[y+x] = false,那么就说明此时可以放置皇后,然后将g[x][y] = 'Q',再将ol[y] = dg[y-x+n] = udg[y+x] = true,然后递归的处理下一行(即dfs(x+1));当第一轮递归结束后,此时我们就把棋子进行回溯操作,把所有的东西恢复到初始状态即棋盘全部变为‘.’和修改过的布尔类型数组变为false;第一次处理是将第一行第一列放第一个皇后,然后递归处理后续情况;第二次处理是将第一行第二列放第一个皇后,递归处理最后的情况;最后知道第一行最后一列放第一个皇后,此时我们就将所有的情况都考虑到了。
当引入4个皇后到4*4棋盘的情况:

图1.2模拟(一)
图1.2展示当 我们让第一行第一列放置第一个皇后所出现的情形,无法得到放置4个皇后的情况。
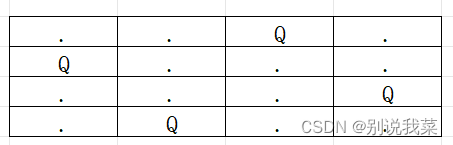
图1.3模拟(二)
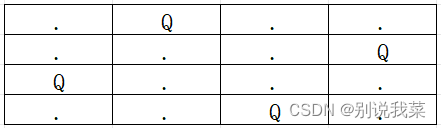
图1.4模拟(三)
图1.3和图1.4模拟的是当皇后分别放在 第一行第二列和第一行第三列且成功在棋盘上放置4个皇后的情况。
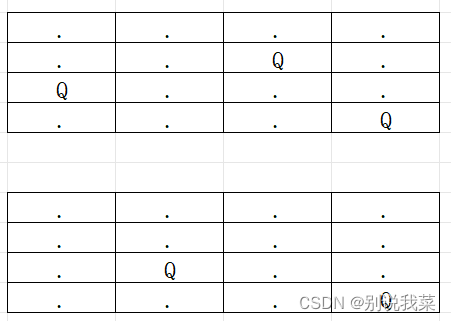
图1.5模拟(四)
图1.5模拟的是当皇后放在第一行第四列的所有情况,无法在棋盘上放置4个皇后。
三、使用步骤
1.代码如下
import java.io.*;
import java.util.*;
public class n皇后问题 {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static int n = 0;
//存储路径
static char[][] g;
//列
static boolean[] col;
//斜对角线
static boolean[] dg;
//斜写对角线
static boolean[] udg;
public static void main(String[] args) {
Scanner sc = new Scanner(br);
n = sc.nextInt();
g = new char[20][20];
col = new boolean[20];
dg = new boolean[20];
udg = new boolean[20];
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
g[i][j] = '.';
}
}
dfs(0);
pw.flush();
}
public static void dfs(int u){
//当u=n时说明我们找到一种方案
if(u == n){
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
pw.print(g[i][j]);
}
pw.println();
}
pw.println();
return;
}
//行数
int x = u;
//枚举每一列
for(int y = 0;y < n;y++){
// 列 对角线 反对角线
if(col[y] == false && dg[y-x+n] == false && udg[y+x] == false){
g[x][y] = 'Q';
//表示这些位置不能放了
col[y] = dg[y-x+n] = udg[y+x] = true ;
dfs(x+1);
//回溯
g[x][y] = '.';
col[y] = dg[y-x+n] = udg[y+x] = false;
}
}
}
}
2.读入数
43.代码运行结果
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..总结
我们主要理解dfs的原理,懂得如何套用dfs代码模板,最重要的不要忘记进行回溯操作。