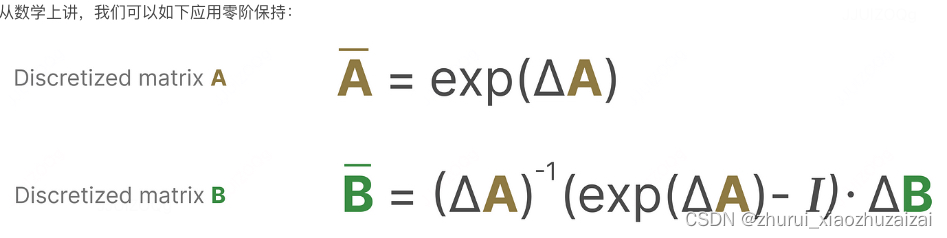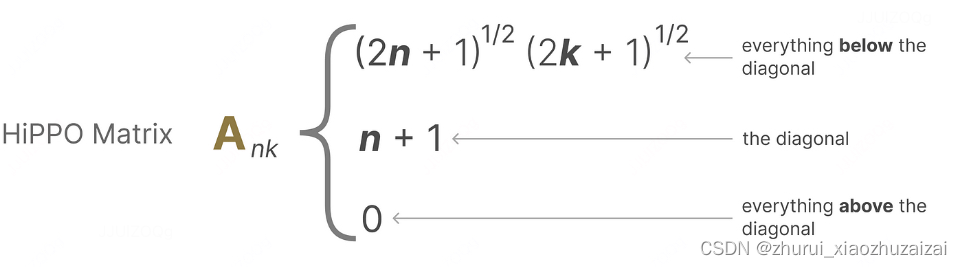1 mamba解决什么问题
Transformer的问题,其计算复杂度与序列长度的平方成正比,导致在处理长序列时效率低下。
Transformer 的注意力创建一个矩阵,将每个 token 与之前的每个 token 进行比较。矩阵中的权重由 token 对之间的相关性决定。
长度为 L 的序列生成 token 大约需要 L² 的计算量,如果序列长度增加,计算量会平方级增长。因此,需要重新计算整个序列是 Transformer 体系结构的主要瓶颈。
RNN 的问题:
每个隐藏状态都是之前所有隐藏状态的聚合。这会导致随着时间的推移,RNN 会忘记更久的信息,因为它只考虑前一个状态。
并且 RNN 的这种顺序性产生了另一个问题。训练不能并行进行,因为它需要按顺序完成每一步。
人们一直在寻找一种既能像 Transformer 那样并行化训练,能够记住先前的信息,又能在推理时时间是随序列长度线性增长的模型,Mamba 就是这样应运而生的。
Mamba基于“选择性状态空间模型”(selective state space model),在处理长序列时展现出更高的效率和性能。
Mamba的主要创新点包括:
线性时间复杂度:与Transformer不同,Mamba在序列长度方面实现了线性时间运行,特别适合处理非常长的序列。
选择性状态空间:Mamba利用选择性状态空间,能够更高效和有效地捕获相关信息,特别是在长序列中。
硬件感知算法:Mamba使用针对现代硬件(尤其是GPU)优化的并行算法,减少内存需求,提高计算效率。
简化架构:Mamba的结构比Transformer更简单,它去除了传统的注意力和MLP块,提供了更好的可扩展性和性能。
在性能方面,Mamba在语言、音频和基因组学等多个领域表现出色,能够与大型Transformer模型相媲美甚至超越。特别是在语言建模中,Mamba展示了卓越的性能,其预训练模型和代码已公开供社区使用。
2 mamba
论文地址:https://arxiv.org/abs/2312.00752
模型地址:state-spaces (State Space Models)
代码地址:https://github.com/state-spaces/mamba
2.1 Mamba的主要特点
选择机制(Selection Mechanism):Mamba采用选择机制来改进状态空间模型(SSM),允许模型基于输入内容有选择地传播或遗忘信息,从而增强了模型的表达能力。
硬件感知算法(Hardware-aware Algorithm):为使选择机制SSM在硬件上高效运行,Mamba设计了融合了内核和重新计算的硬件感知算法,避免了中间状态的存储,提高了速度和内存效率。
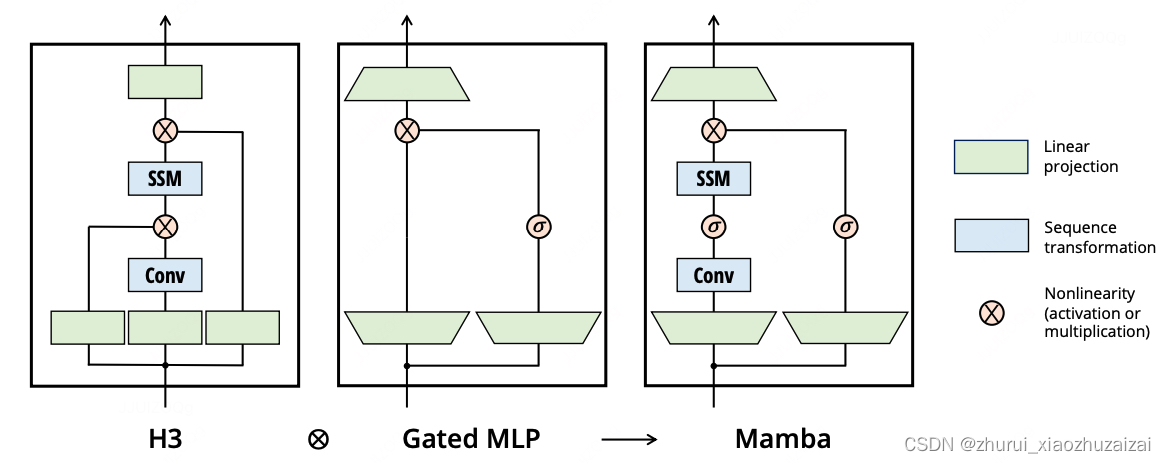
简化的架构(Simplified Architecture):Mamba将H3中的SSM块和Transformer中的MLP块合并为一个简化的块,重复堆叠这些块形成整体架构。这种简化的设计提高了训练和推理的效率。
2.2 SSM->HIPPO->S4
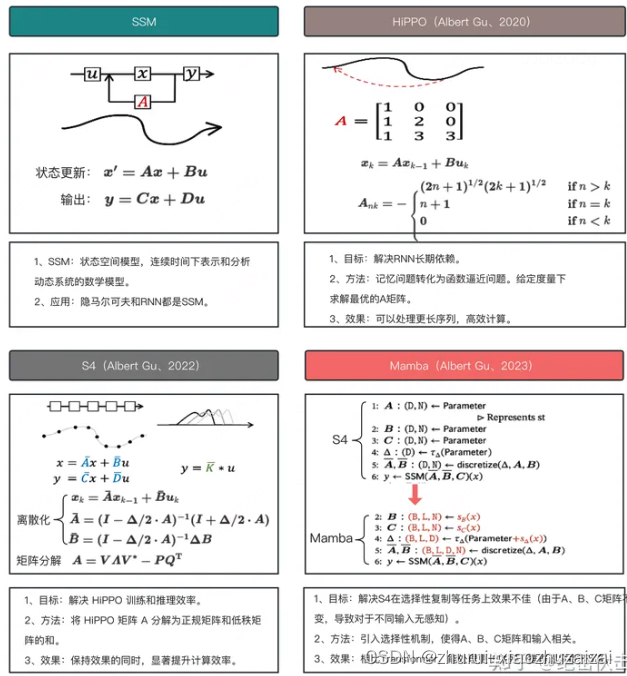
2.2.1 标准SSM
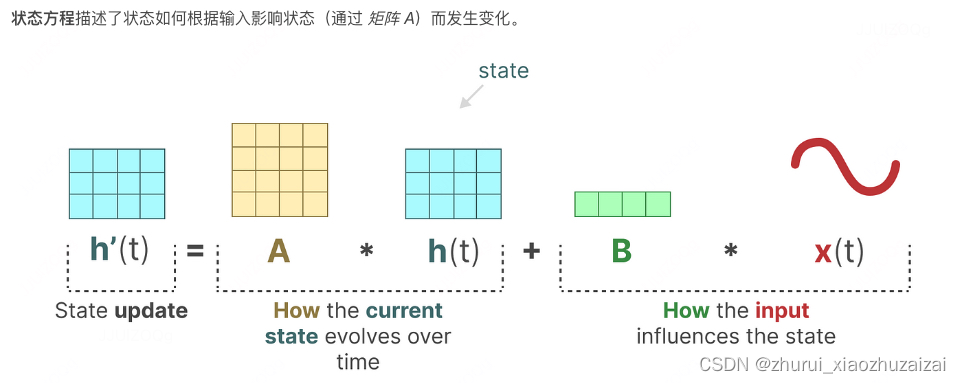
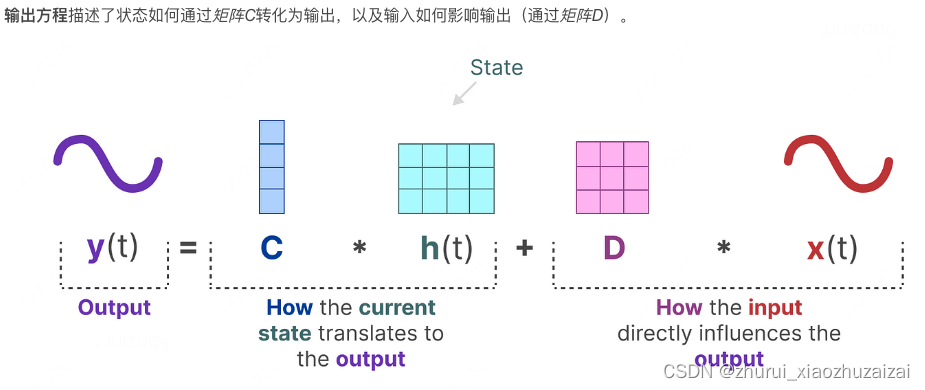
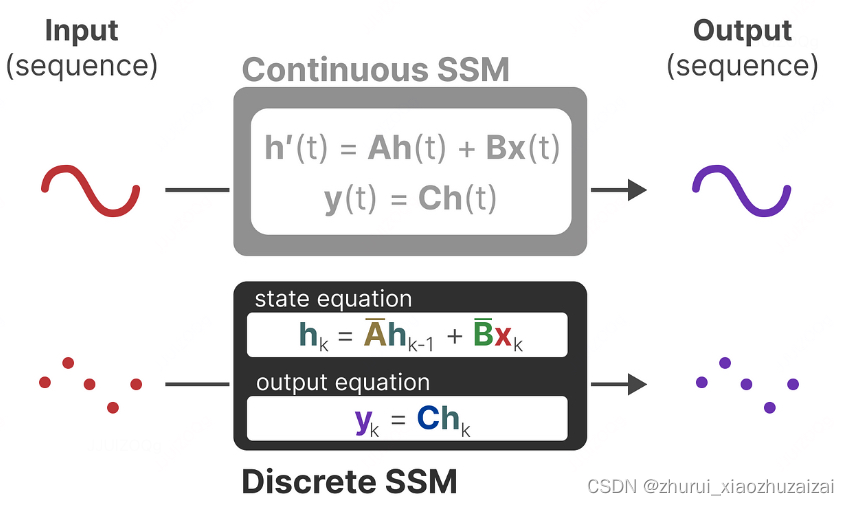
状态空间模型(State Space Models,SSM)由简单的方程定义。它将一维输入信号 x(t)映射到 N 维潜在状态 h(t)然后再投影到一维输出信号 y(t)。
SSM的两个方程:状态方程x(t)与输出方程y(t)
总之,SSM的关键是找到:状态表示(state representation)—— h(t),以便结合「其与输入序列」预测输出序列
(矩阵A描述了所有内部状态如何连接影响当前内部状态)
(矩阵B描述了当前输入如何影响当前内部状态)
(矩阵C描述了所有内部状态如何影响输出)
(矩阵D描述了当前输入如何影响输出)
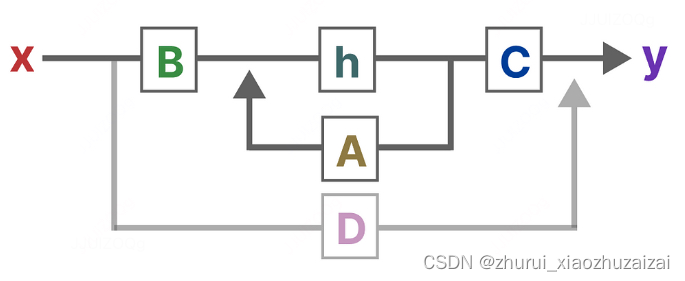
简化的结构:
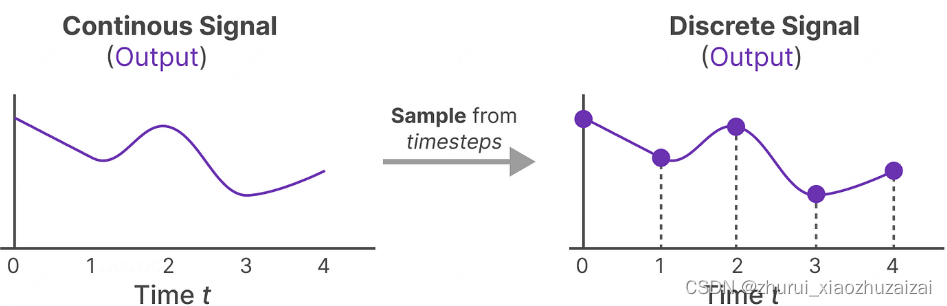
2.2.2 零阶保持技术–从连续信号到离散信号
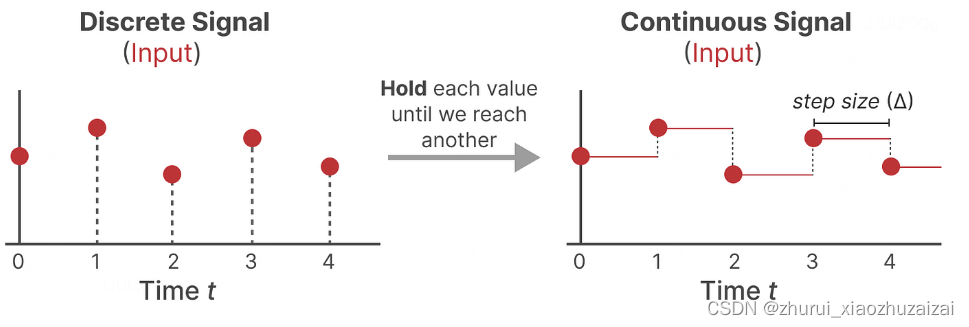
如果你有一个连续信号,找到状态表示***h(t)***在分析上是具有挑战性的。此外,由于我们通常有离散输入(如文本序列),我们希望将模型离散化。
为此,我们使用零阶保持技术。它的工作原理如下。首先,每当我们接收到一个离散信号时,我们保持其值,直到我们接收到一个新的离散信号。这个过程创建了一个连续信号,SSM可以使用:
我们保持值的时间由一个新的可学习参数表示,称为步长 ∆。它表示输入的分辨率。
现在,我们有了连续信号作为输入,我们可以生成连续输出,并根据输入的时间步长仅对值进行采样。
在这里,矩阵A和B现在表示模型的离散化参数。
我们使用k而不是t来表示离散化的时间步长,并且在引用连续SSM和离散SSM时更加清晰。
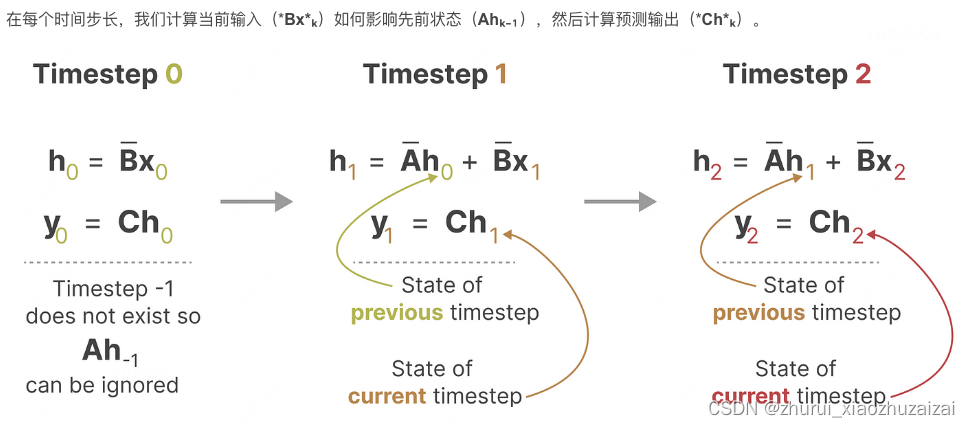
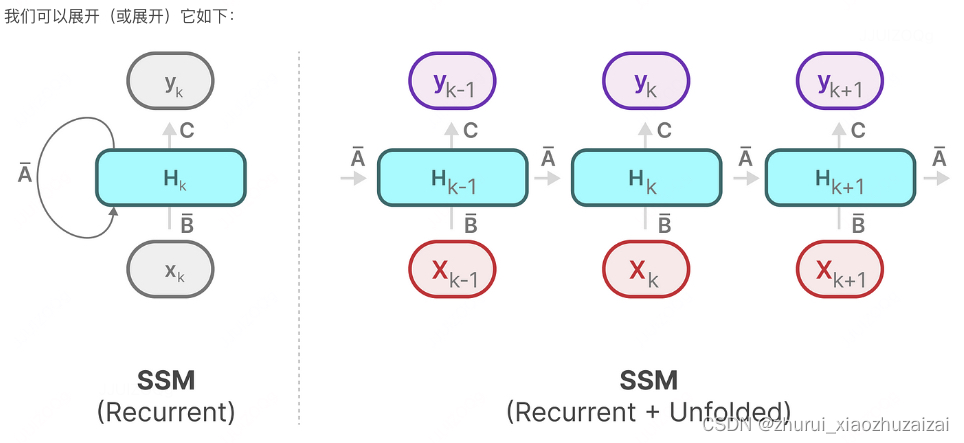
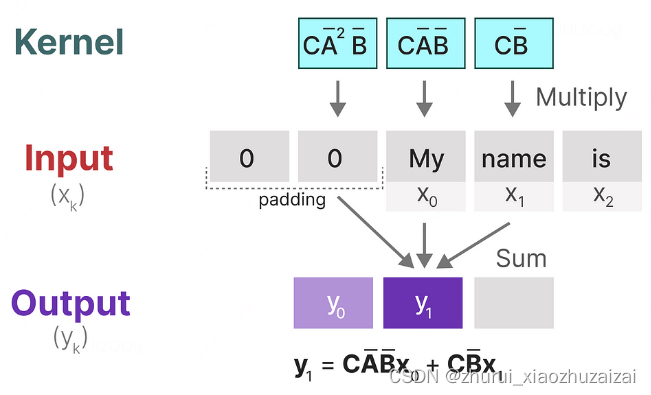
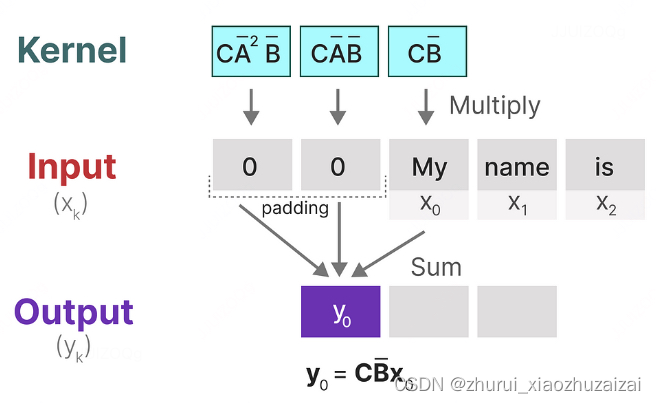
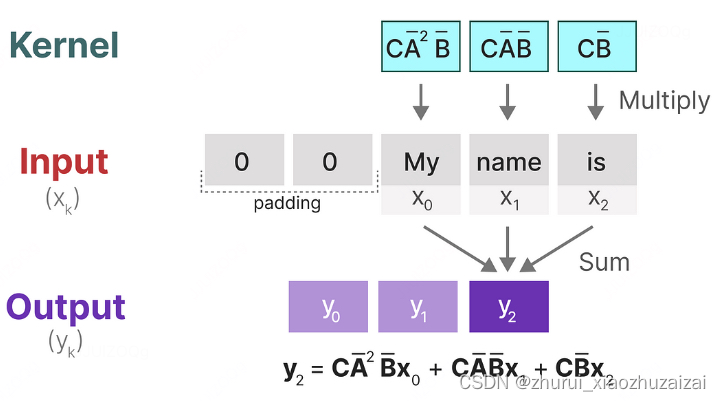
离散SSM计算–像RNN一样
2.2.3 长距离依赖问题的解决之道——HiPPO
可以说,SSM公式中最重要的一个方面是矩阵A。正如我们之前在循环表示中看到的那样,它捕捉了关于先前状态的信息,以构建新状态。
由于矩阵A只记住之前的几个token和捕获迄今为止看到的每个token之间的区别,特别是在循环表示的上下文中,因为它只回顾以前的状态
Hippo的全称是High-order Polynomial Projection Operator,
其对应的论文为:HiPPO: Recurrent Memory with Optimal Polynomial Projections
作者讨论了如何处理长距离依赖(Long-Range Dependencies,LRDs)的问题,LRDs 是序列建模中的一个关键挑战,因为它们涉及到在序列中跨越大量时间步的依赖关系。
作者指出,基本的 SSM 在实际应用中表现不佳,特别是在处理 LRDs 时。这是因为线性一阶常微分方程(ODEs)的解通常是指数函数,这可能导致梯度在序列长度上呈指数级增长,从而引发梯度消失或爆炸的问题。
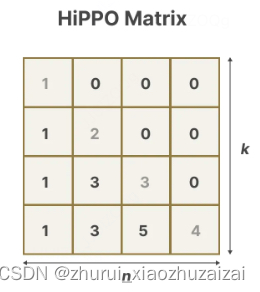
为了解决这个问题,作者利用了 HiPPO 理论。HiPPO 理论指定了一类特殊的矩阵 A,当这些矩阵被纳入 SSM 的方程中时,可以使状态 x(t) 能够记住输入 u(t) 的历史信息。这些特殊矩阵被称为 HiPPO 矩阵,它们具有特定的数学形式,可以有效地捕捉长期依赖关系。
HiPPO 矩阵的一个关键特性是它们允许 SSM 在数学和实证上捕捉 LRDs。例如,通过将随机矩阵 A 替换为 HiPPO 矩阵,可以在序列 MNIST 基准测试上显著提高 SSM 的性能。
它使用矩阵A来构建一个状态表示,能够很好地捕捉最近的标记,并衰减较旧的标记。其公式可以表示如下:
使用HiPPO构建矩阵A被证明比将其初始化为随机矩阵要好得多。因此,与初始标记相比,它更准确地重构了新的信号(最近的标记)。
HiPPO矩阵背后的思想是它产生一个隐藏状态,可以记住其历史。
从数学上讲,它通过跟踪Legendre多项式的系数来实现这一点,这使得它能够近似所有先前的历史。
2.2.4 S4——HiPPO的应用
然后,HiPPO被应用于我们之前看到的循环和卷积表示,以处理长距离依赖关系。结果是Sequences的结构化状态空间(S4),这是一类可以高效处理长序列的SSM。
且对矩阵A 做了改进
它由三个部分组成:
状态空间模型
用于处理长距离依赖关系的HiPPO
用于创建循环和卷积表示的离散化
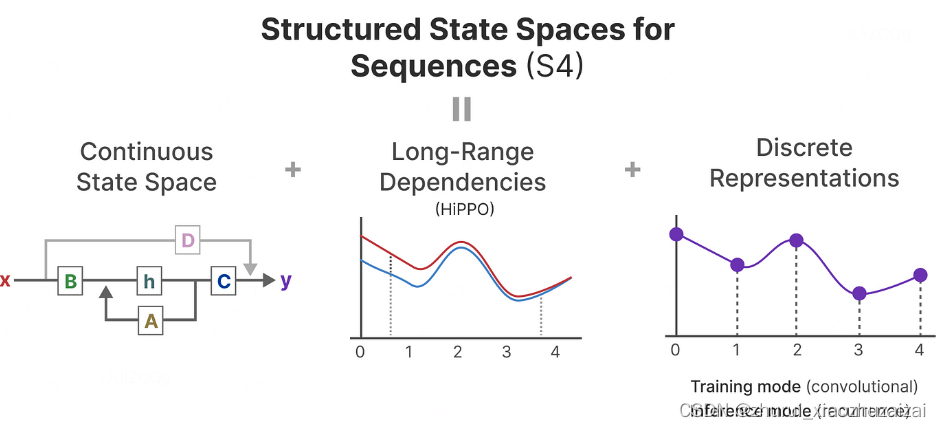
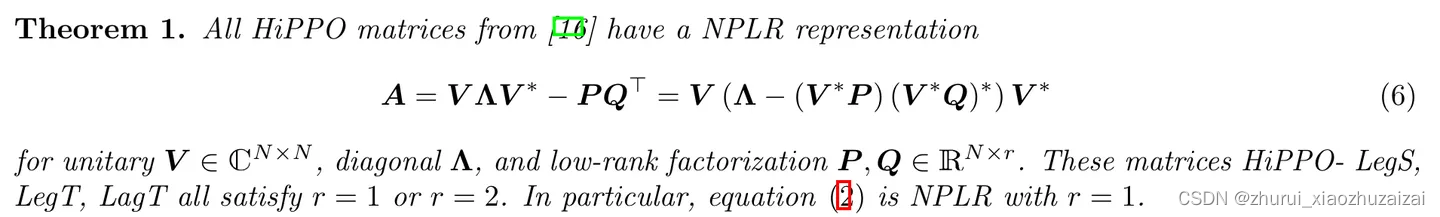
S4 是 HiPPO 的后续工作,论文名称为:Efficiently Modeling Long Sequences with Structured State Spaces。
S4 的主要工作是将 HiPPO 中的矩阵 A(称为 HiPPO 矩阵)转换为正规矩阵(正规矩阵可以分解为对角矩阵)和低秩矩阵的和,以此提高计算效率。
S4 通过这种分解,将计算复杂度降低到了O(N+L) ,其中 N 是 HiPPO 矩阵的维度,L 是序列长度。
在处理长度为 16000 的序列的语音分类任务中,S4 模型将专门设计的语音卷积神经网络(Speech CNNs)的测试错误率降低了一半,达到了1.7%。相比之下,所有的循环神经网络(RNN)和 Transformer 基线模型都无法学习,错误率均在70%以上。
S4 在推理时,使用递归形式,每次只需要和上一个状态进行计算,具有和 RNN 相似的推理效率。
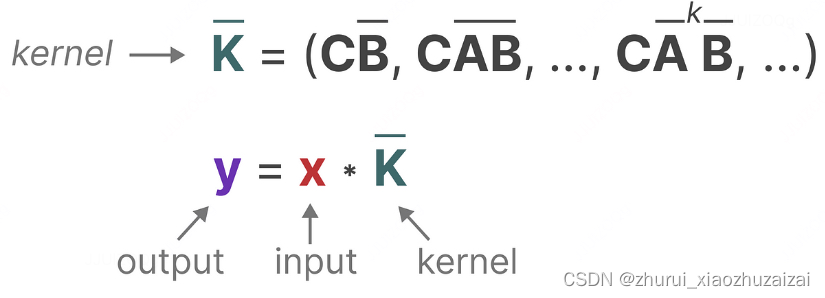
由于离散时间 SSM 的递归性质,它在硬件上进行训练时存在效率问题。因此,作者将离散时间 SSM 的递归方程转换为离散卷积的形式。通过展开递归方程,可以得到一个卷积核,这个卷积核可以用来在序列数据上应用卷积操作。这种转换允许 SSM 利用快速傅里叶变换(FFT)等高效的卷积计算方法,从而在训练过程中提高计算效率。
为什么对角化可以减少 SSM 计算复杂度
- 为了进一步提升计算效率,作者讨论了对角化在计算离散时间状态空间模型(SSM)中的应用,以及为什么直接应用对角化方法在实践中并不可行。
- 对角化是一种线性代数技术,它可以将一个矩阵转换为对角形式,从而简化矩阵的乘法和其他运算。在 SSM 的上下文中,对角化可以显著减少计算复杂度,因为对角矩阵的幂运算(如在递归方程中出现的)可以通过简单的元素指数运算来完成。
直接对角化 HiPPO 矩阵导致数值溢出
S4 参数化:正规矩阵+低秩矩阵
虽然矩阵 A不能直接对角化,但是可以表示为正规矩阵+低秩矩阵。

HiPPO 矩阵是 S4 模型中用于处理长距离依赖(LRDs)的关键组件。
在这一节中,作者通过以下几个方面的实验来验证 HiPPO 矩阵的重要性:
- HiPPO 初始化:作者首先研究了不同初始化方法对 SSM 性能的影响,包括随机高斯初始化、HiPPO 初始化以及随机对角高斯矩阵初始化。实验结果表明,HiPPO 初始化在提高模型性能方面起到了关键作用。
- HiPPO 矩阵是否可训练:作者还探讨了 HiPPO 矩阵固定以及可训练的效果。他们发现,固定 HiPPO 和可训练的差异不大。
- NPLR SSMs:作者进一步研究了在没有 HiPPO 矩阵的情况下,随机 NPLR(Normal Plus Low-Rank,正规+低秩矩阵)的表现。结果表明,即使在 NPLR 形式下,这些随机矩阵的性能仍然不佳,这验证了 HiPPO 矩阵在 S4 模型中的核心作用。
通过这些消融实验,作者强调了 HiPPO 矩阵在 S4 模型中的重要性。这些实验结果不仅证实了 HiPPO 矩阵在处理长距离依赖方面的有效性,而且也表明了它在提升模型整体性能方面的关键作用。这些发现对于理解 S4 模型的设计和优化至关重要。
2.3 mamba的SSM【S4–>S6】
虽然 S4 在保证了计算效率的同时,优化了长距离依赖问题。
但是由于矩阵 A,B,C是固定不变的,和输入 token 无关,这就导致了 S4 在一些合成任务上效果不佳
状态空间模型,甚至是S4(结构化状态空间模型),在某些对语言建模和生成至关重要的任务上表现不佳,即关注或忽略特定输入的能力。
- 由于(循环/卷积)SSM 是线性时间不变的,对于 SSM生成的每个 token,矩阵 A、B 和 C 都是相同的。它无法选择从历史中回忆哪些之前的 token。无论输入 u 是什么,矩阵 B 都保持不变,因此与 u 无关,同理,无论输入是什么,A 和 C 也不变,这就是我们上面说的静态。即矩阵 A、B 和 C 的静态性质导致内容感知方面的问题。
为了解决上面的问题,作者提出了一种新的选择性 SSM(Selective State Space Models,简称 S6 或 Mamba)。这种模型通过让 SSM 的矩阵 A、B、C 依赖于输入数据,从而实现了选择性。这意味着模型可以根据当前的输入动态地调整其状态,选择性地传播或忽略信息。Mamba 集成了 S4 和 Transformer 的精华,一个更加高效(S4),一个更加强大(Transformer)。
Mamba: Linear-Time Sequence Modeling with Selective State Spaces
在本节中,我们将介绍 Mamba 的两大主要贡献:
一种选择性扫描算法,该算法允许模型过滤(不)相关信息;
一种硬件感知算法,该算法允许通过并行扫描、内核融合和重新计算来高效存储(中间)结果。
它们共同创建了选择性 SSM 或 S6 模型,这些模型可以像自注意力一样用于创建 Mamba 块。
选择性 SSM,这种架构通常被称为选择性 SSM或S6模型,因为它本质上是使用选择性扫描算法计算的 S4 模型。
S4 和 选择性 SSM 的核心区别在于,它们将几个关键参数(∆, B, C)设定为输入的函数,并且伴随着整个 tensor 形状的相关变化。特别是,这些参数现在具有一个长度维度 L,这意味着模型已经从时间不变(time-invariant)转变为时间变化(time-varying)。
最后作者选择把 A设成了与输入无关,作者给出的解释是离散化之后 A¯=exp(ΔA),Δ的数据依赖能够让整体的 A¯与输入相关。
它们一起选择性地选择在隐藏状态中保留什么和忽略什么,因为它们现在依赖于输入。
较小的步长 ∆ 导致忽略特定单词,而更大的步长 ∆ 则更多地关注输入单词而不是上下文:
因为现在的参数 A,B,C都是输入相关了,所以不再是线性时间不变系统,也就失去了卷积的性质,不能用 FFT来进行高效训练了。
Mamba 作者采用了一种称为硬件感知的算法,实际上就是用三种经典技术来解决这个问题:
内核融合(kernel fusion)、并行扫描(parallel scan)和重计算(recomputation)。
- 一般的实现会
提前先把大小为 (B,L,D,N)的 A¯,B¯先算出来,
然后把它们从 HBM (high-bandwidth memory 或 GPU memory) 读到SRAM,
然后调用 scan 算子算出 (B,L,D,N)的 output,写到 HBM 里面。
再开一个kernel 把 (B,L,D,N)的 output 以及(B,L,N)的 C 读进来,
multiply and sum with C 得到最后的 (B,L,D)output 。
整个过程的读写是 O(BLDN)。- 而 Mambda 作者的方法是:
把 (Δ,A,B,C)读到 SRAM 里面,总共大小是 O(BLN+DN)
在 SRAM 里面做离散化,得到 (B,L,D,N)的 A¯,B¯
在 SRAM 里面做 scan,得到(B,L,D,N)的 output
multiply and sum with C,得到最后的(B,L,D)output 写入HBM
整个过程的总读写量是 O(BLN),比之前省了 O(N)倍。 backward 的时候就把 A¯,B¯重算一遍,类似于flashattn 重算 attention 分数矩阵的思想。只要重算的时间比读 O(BLND)快就算有效。
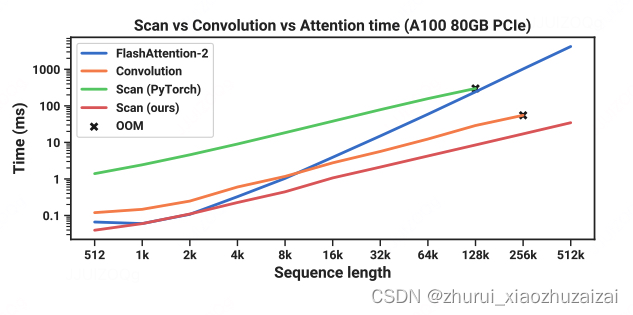
Mamba 的实现比其它方法实现快很多倍,scan 在输入长度 2k 的时候就开始比 FlashAttention 快了,之后越长越快。同时 scan 也比 Convolution 快。