B树(B-tree)
B树(B-tree)是一种自平衡的多路查找树,主要用于磁盘或其他直接存取的辅助存储设备
B树能够保持数据有序,并允许在对数时间内完成查找、插入及删除等操作
这种数据结构常被应用在数据库和文件系统的实现上
B树的特点包括:
B树为了表示节点个数 通常称为 M阶树
1.M阶树每个结点至多有M棵子树(M>=2)
2.每个非根节点至少有 M/2(向上取整)个孩子,至多有M个孩子。
3.每个叶子节点至少有 M/2-1 个关键字,至多有M-1个关键字,并以升序排列
4.所有叶子节点都在同一层
5.非叶子节点的关键字个数等于其孩子数减一
6.所有叶子节点不含有任何信息
按照子节点数 y:非根节点至少有 M/2(向上取整)个孩子,至多有M个孩子
M = 3, 2 <= y <= 3, 因此称为:2-3树
M = 4, 2 <= y <= 4, 因此称为:2-3-4树
M = 5, 3 <= y <= 5, 因此称为:3-5树
M = 7, 4 <= y <= 7, 因此称为:4-7树
B树的高度对于含有n个关键字的m阶B树,其高度为O(log n)
这种数据结构通过减少定位记录时所经历的中间过程,从而加快存取速度
与自平衡的二叉查找树不同,B树为系统大块数据的读写操作做了优化
下面先看 B树节点的定义
class BTNode<T> where T : IComparable<T>
{
private BTNode<T> parentNode; // 父节点
private List<T> keyList; // 关键字向量
private List<BTNode<T>> childList; // 子节点向量(其长度总比key多一)
}
B树每个节点存储的关键字是从小到大有序的:keyList 是从小到大排序的
B树 关键字个数 比 子节点 个数少 1 个,为什么?
因为 关键字 和 子节点 可以理解为这么样一个排序,假设一个 5 阶树的一个节点
childList[0],keyList[0],childList[1],keyList[1],childList[2]
可以看到 子节点 和 关键字 是交替出现的,并且 子节点 比 关键字 个数多 1 个
并且还有一个隐藏的信息
1.子树中所有关键字的值,比其右侧的关键字都小
2.子树中所有关键字的值,比其左侧的关键字都大
什么意思呢?
1.(childList[0] 子树下所有节点的关键字) 小于 keyList[0]
2. keyList[0] 小于 (childList[1] 子树下所有节点的关键字)
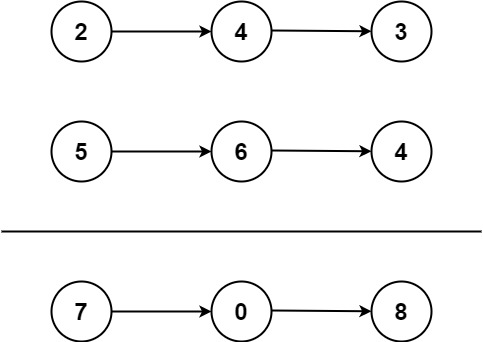
看下图 一个 5阶树

Node0 包含 三个关键字(25,39,66),四个子节点(Node1,Node2,Node3,Node4)
25 对应 keyList[0]
39 对应 keyList[1]
66 对应 keyList[2]
Node0 包含 两个关键字 (5, 13) < 25
Node1 包含 两个关键字 25 < (28, 30) < 39
Node2 包含 两个关键字 39 < (40, 55) < 66
Node3 包含 两个关键字 66 < (67, 68, 90)
B树在操作 插入、删除的过程中往往会导致
上溢:节点个数大于 B树限制
下移:节点个数小于 B树限制
需要通过一系列操作将树恢复平衡
B树操作逻辑
查询: number
1.根节点作为当前节点
2. number 顺次与当前节点的关键字作比较
如果 number < keyList[index],则 number 一定在 childList[index],令当前节点= childList[index] 循环执行 2
如果 number = keyList[index],则 在关键字中找到 了number,查询完成,返回节点
如果 number > keyList[index], index++,如果 index >= childList.Count,查找失败,返回,否则继续循环执行 2 ,比较下一个 关键字 keyList[index]
我在查询操作逻辑中隐含保留了一个 hot 节点,这个 hot 节点是最接近 number 的节点,如果查询成功,则 hot 不再起作用,如果查询失败,在 插入操作中 是有用处的
插入: number
1.先执行查询操作,如果查询到节点,则说明已经存在,不再添加,返回
2.查询逻辑中 保存的 hot 节点是最接近 numbe 的节点,我们将 number 插入到hot节点
3.令 number 与 keyList 中的数据比较
如果 keyList[i] < number, 将 number 插入到 keyList第 i + 1 位置,然后 childList 第 i + 2 位置插入一个空节点
如果 keyList 中的关键字 > number,将 number 插入到 keyList 第 0 个位置,然后 childList 第 1 个位置插入一个空节点
4. 如果 hot 节点发生上溢,做分裂处理
C#代码实现如下
B树节点定义
/// <summary>
/// B-树节点定义
/// </summary>
/// <typeparam name="T"></typeparam>
class BTNode<T> where T : IComparable<T>
{
private BTNode<T> parentNode; // 父节点
private List<T> keyList; // 关键字向量
private List<BTNode<T>> childList; // 子节点向量(其长度总比key多一)
public BTNode()
{
keyList = new List<T>();
childList = new List<BTNode<T>>();
childList.Insert(0, null);
}
public BTNode(T t, BTNode<T> lc, BTNode<T> rc)
{
parentNode = null;
keyList.Insert(0, t);
// 左右孩子
childList.Insert(0, lc);
childList.Insert(1, rc);
if (null != lc)
{
lc.parentNode = this;
}
if (null != rc)
{
rc.parentNode = this;
}
}
public BTNode<T> ParentNode
{
get { return parentNode; }
set { parentNode = value; }
}
private List<T> KeyList
{
get { return keyList; }
set { keyList = value; }
}
public int KeyCount
{
get { return KeyList.Count; }
}
public void InsertKey(int index, T key)
{
KeyList.Insert(index, key);
}
public T GetKey(int index)
{
return KeyList[index];
}
public void RemoveKeyAt(int index)
{
KeyList.RemoveAt(index);
}
public void SetKey(int index, T key)
{
KeyList[index] = key;
}
private List<BTNode<T>> ChildList
{
get { return childList; }
set { childList = value; }
}
public void InsertChild(int index, BTNode<T> node)
{
ChildList.Insert(index, node);
if (null != node)
{
node.parentNode = this;
}
}
public BTNode<T> GetChild(int index)
{
return ChildList[index];
}
public void AddChild(BTNode<T> node)
{
InsertChild(ChildList.Count, node);
}
public BTNode<T> RemoveChildAt(int index)
{
BTNode<T> node = ChildList[index];
ChildList.RemoveAt(index);
return node;
}
public void SetChild(int index, BTNode<T> node)
{
ChildList[index] = node;
}
public int ChildCount
{
get { return ChildList.Count; }
}
}
B树实现
/// <summary>
/// B-树
/// </summary>
/// <typeparam name="T"></typeparam>
class BTree<T> where T : IComparable<T>
{
private int _order; // 介次
protected BTNode<T> _root; // 跟节点
protected BTNode<T> _hot; // search() 最后访问的非空节点位置
public BTree(int order)
{
_order = order;
}
public BTNode<T> Root
{
get { return _root; }
set { _root = value; }
}
/// <summary>
/// 查找
/// </summary>
public BTNode<T> Search(T t)
{
BTNode<T> v = Root; // 从根节点触发
_hot = null;
while (null != v)
{
int index = -1;
for (int i = 0; i < v.KeyCount; ++i)
{
int compare = v.GetKey(i).CompareTo(t);
if (compare <= 0)
{
index = i;
if (compare == 0)
{
break;
}
}
}
// 若成功,则返回
if (index >= 0 && v.GetKey(index).CompareTo(t) == 0)
{
return v;
}
_hot = v;
// 沿引用转至对应的下层子树,并载入其根
v = v.ChildCount > (index + 1) ? v.GetChild(index + 1) : null;
}
// 若因 null == v 而退出,则意味着抵达外部节点
return null; // 失败
}
/// <summary>
/// 插入
/// </summary>
public bool Insert(T t)
{
BTNode<T> node = Search(t);
if (null != node)
{
return false;
}
int index = -1;
for (int i = 0; i < _hot.KeyCount; ++i)
{
int compare = _hot.GetKey(i).CompareTo(t);
if (compare <= 0)
{
index = i;
if (compare == 0)
{
break;
}
}
}
_hot.InsertKey(index + 1, t); // 将新关键码插至对应的位置
_hot.InsertChild(index + 2, null); // 创建一个空子树指针
SolveOverflow(_hot); // 如发生上溢,需做分裂
return true;
}
/// <summary>
/// 删除
/// </summary>
public bool Remove(T t)
{
BTNode<T> node = Search(t);
if (null == node)
{
return false;
}
int index = -1;
for (int i = 0; i < node.KeyCount; ++i)
{
if(node.GetKey(i).CompareTo(t) == 0)
{
index = i;
break;
}
}
// node 不是叶子节点
if (null != node.GetChild(0))
{
BTNode<T> u = node.GetChild(index + 1); // 在右子树中一直向左,即可
while (null != u.GetChild(0))
{
u = u.GetChild(0); // 找到 t 的后继(必需于某叶节点)
}
// 至此,node 必然位于最底层,且其中第 r 个关键码就是待删除者
node.SetKey(index, u.GetKey(0));
node = u; // 并与之交换位置
index = 0;
}
node.RemoveKeyAt(index);
node.RemoveChildAt(index + 1);
SolveUnderflow(node); // 如有必要,需做旋转或合并
return false;
}
/// <summary>
/// 上溢:因插入而上溢后的分裂处理
/// </summary>
private void SolveOverflow(BTNode<T> v)
{
if (_order >= v.ChildCount)
{
return; //递归基:当前节点并未上溢
}
int s = _order / 2; //轴点(此时应有_order = key.Count = child.Count - 1)
BTNode<T> u = new BTNode<T>(); //注意:新节点已有一个空孩子
for (int j = 0; j < _order - s - 1; j++)
{ //v右侧_order-s-1个孩子及关键码分裂为右侧节点u
BTNode<T> node = v.GetChild(s + 1);
v.RemoveChildAt(s + 1);
u.InsertChild(j, node); //逐个移动效率低
T key = v.GetKey(s + 1);
v.RemoveKeyAt(s + 1);
u.InsertKey(j, key); //此策略可改进
}
BTNode<T> node2 = v.GetChild(s + 1);
v.RemoveChildAt(s + 1);
u.SetChild(_order - s - 1, node2); //移动v最靠右的孩子
if (null != u.GetChild(0)) //若u的孩子们非空,则
{
for (int j = 0; j < _order - s; j++) //令它们的父节点统一
{
u.GetChild(j).ParentNode = u; //指向u
}
}
BTNode<T> p = v.ParentNode; //v当前的父节点p
if (null == p)
{
_root = p = new BTNode<T>();
p.SetChild(0, v);
v.ParentNode = p;
} //若p空则创建之
int index = -1;
for (int i = 0; i < p.KeyCount; ++i)
{
int compare = p.GetKey(i).CompareTo(v.GetKey(0));
if (compare <= 0)
{
index = i;
if (compare == 0)
{
break;
}
}
}
int r = 1 + index; //p中指向u的指针的秩
T key2 = v.GetKey(s);
v.RemoveKeyAt(s);
p.InsertKey(r, key2); //轴点关键码上升
p.InsertChild(r + 1, u);
u.ParentNode = p; //新节点u与父节点p互联
SolveOverflow(p); //上升一层,如有必要则继续分裂——至多递归O(logn)层
}
/// <summary>
/// 下溢:因删除而下溢后的合并处理
/// </summary>
/// <param name="node"></param>
private void SolveUnderflow(BTNode<T> v)
{
if ((_order + 1) / 2 <= v.ChildCount) return; //递归基:当前节点并未下溢
BTNode<T> p = v.ParentNode;
if (null == p)
{ //递归基:已到根节点,没有孩子的下限
if (v.KeyCount <= 0 && null != v.GetChild(0))
{
//但倘若作为树根的v已不含关键码,却有(唯一的)非空孩子,则
/*DSA*/
_root = v.GetChild(0);
_root.ParentNode = null; //这个节点可被跳过
v.SetChild(0, null); //release(v); //并因不再有用而被销毁
} //整树高度降低一层
return;
}
int r = 0;
while (p.GetChild(r) != v)
{
r++;
}
//确定v是p的第r个孩子——此时v可能不含关键码,故不能通过关键码查找
//另外,在实现了孩子指针的判等器之后,也可直接调用Vector::find()定位
/*DSA*/
// 情况1:向左兄弟借关键码
if (0 < r)
{ //若v不是p的第一个孩子,则
BTNode<T> ls = p.GetChild(r - 1); //左兄弟必存在
if ((_order + 1) / 2 < ls.ChildCount)
{ //若该兄弟足够“胖”,则
/*DSA*/
v.InsertKey(0, p.GetKey(r - 1)); //p借出一个关键码给v(作为最小关键码)
T key = ls.GetKey(ls.KeyCount - 1);
ls.RemoveKeyAt(ls.KeyCount - 1);
p.SetKey(r - 1, key); //ls的最大关键码转入p
BTNode<T> node = ls.GetChild(ls.ChildCount - 1);
ls.RemoveChildAt(ls.ChildCount - 1);
//同时ls的最右侧孩子过继给v
//作为v的最左侧孩子
v.InsertChild(0, node);
return; //至此,通过右旋已完成当前层(以及所有层)的下溢处理
}
} //至此,左兄弟要么为空,要么太“瘦”
// 情况2:向右兄弟借关键码
if (p.ChildCount - 1 > r)
{ //若v不是p的最后一个孩子,则
BTNode<T> rs = p.GetChild(r + 1); //右兄弟必存在
if ((_order + 1) / 2 < rs.ChildCount)
{ //若该兄弟足够“胖”,则
/*DSA*/
v.InsertKey(v.KeyCount, p.GetKey(r)); //p借出一个关键码给v(作为最大关键码)
T key = rs.GetKey(0);
rs.RemoveKeyAt(0);
p.SetKey(r, key); //rs的最小关键码转入p
BTNode<T> node = rs.GetChild(0);
rs.RemoveChildAt(0);
v.InsertChild(v.ChildCount, node);
//同时rs的最左侧孩子过继给v
if (null != v.GetChild(v.ChildCount - 1)) //作为v的最右侧孩子
{
v.GetChild(v.ChildCount - 1).ParentNode = v;
}
return; //至此,通过左旋已完成当前层(以及所有层)的下溢处理
}
} //至此,右兄弟要么为空,要么太“瘦”
// 情况3:左、右兄弟要么为空(但不可能同时),要么都太“瘦”——合并
if (0 < r)
{ //与左兄弟合并
/*DSA*/
BTNode<T> ls = p.GetChild(r - 1); //左兄弟必存在
T key = p.GetKey(r - 1);
p.RemoveKeyAt(r - 1);
ls.InsertKey(ls.KeyCount, key);
p.RemoveChildAt(r);
//p的第r - 1个关键码转入ls,v不再是p的第r个孩子
BTNode<T> node = v.GetChild(0);
v.RemoveChildAt(0);
ls.InsertChild(ls.ChildCount, node);//v的最左侧孩子过继给ls做最右侧孩子
while (v.KeyCount > 0)
{ //v剩余的关键码和孩子,依次转入ls
T key2 = v.GetKey(0);
v.RemoveKeyAt(0);
ls.InsertKey(ls.KeyCount, key2);
BTNode<T> node2 = v.GetChild(0);
v.RemoveChildAt(0);
ls.InsertChild(ls.ChildCount, node2);
}
//release(v); //释放v
}
else
{ //与右兄弟合并
/*DSA*/
// printf(" ... case 3R\n");
BTNode<T> rs = p.GetChild(r + 1); //右兄弟必存在
T key = p.GetKey(r);
p.RemoveKeyAt(r);
rs.InsertKey(0, key); p.RemoveChildAt(r);
//p的第r个关键码转入rs,v不再是p的第r个孩子
BTNode<T> node = v.GetChild(v.ChildCount - 1);
v.RemoveChildAt(v.ChildCount - 1);
rs.InsertChild(0, node);
if (null != rs.GetChild(0))
{
rs.GetChild(0).ParentNode = rs; //v的最左侧孩子过继给ls做最右侧孩子
}
while (v.KeyCount > 0)
{ //v剩余的关键码和孩子,依次转入rs
T key2 = v.GetKey(v.KeyCount - 1);
v.RemoveKeyAt(v.KeyCount - 1);
rs.InsertKey(0, key2);
BTNode<T> node2 = v.GetChild(v.ChildCount - 1);
v.RemoveChildAt(v.ChildCount - 1);
rs.InsertChild(0, node2);
if (null != rs.GetChild(0))
{
rs.GetChild(0).ParentNode = rs;
}
}
//release(v); //释放v
}
SolveUnderflow(p); //上升一层,如有必要则继续分裂——至多递归O(logn)层
}
/// <summary>
/// 层序遍历,获取所有节点,切是按照每一层节点返回
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
public List<List<BTNode<T>>> TraverseLevelList(BTNode<T> node)
{
List<List<BTNode<T>>> listResult = new List<List<BTNode<T>>>();
if (null == node)
{
return listResult;
}
Queue<BTNode<T>> queue = new Queue<BTNode<T>>();
queue.Enqueue(node);
while (queue.Count > 0)
{
int count = queue.Count;
List<BTNode<T>> list = new List<BTNode<T>>();
while(count > 0)
{
--count;
node = queue.Dequeue();
if (null == node)
{
continue;
}
list.Add(node);
for (int i = 0; i < node.ChildCount; ++i)
{
queue.Enqueue(node.GetChild(i));
}
}
listResult.Add(list);
}
return listResult;
}
/// <summary>
/// 层序遍历,获取所有节点
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
public List<BTNode<T>> TraverseLevel(BTNode<T> node)
{
List<BTNode<T>> list = new List<BTNode<T>>();
if (null == node)
{
return list;
}
Queue<BTNode<T>> queue = new Queue<BTNode<T>>();
queue.Enqueue(node);
while (queue.Count > 0)
{
node = queue.Dequeue();
if (null == node)
{
continue;
}
list.Add(node);
for (int i = 0; i < node.ChildCount; ++i)
{
queue.Enqueue(node.GetChild(i));
}
}
return list;
}
}