目录
前言
何为Stable Diffusion模型?
Stable Diffusion工作原理:
Stable Diffusion模型的应用场景
Stable Diffusion免费使用网站
stability.ai:
本地部署 Stable Diffusion方法:
StableDiffusion中文网
博主介绍:✌专注于前后端、机器学习、人工智能应用领域开发的优质创作者、秉着互联网精神开源贡献精神,答疑解惑、坚持优质作品共享。本人是掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战,深受全网粉丝喜爱与支持✌有需要可以联系作者我哦!
🍅文末三连哦🍅
👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟
前言
何为Stable Diffusion模型?
Stable Diffusion是最近很🔥的一种图像生成方法。基于潜在扩散的机器学习模型,其主要用于根据文本的描述生成详细的图像。该模型由慕尼黑大学的CompVis研究团体开发,是各种生成性人工神经网络之一,由初创公司StabilityAI、CompVis与Runway合作开发,并得到EleutherAI和LAION的支持。
Stable Diffusion模型主要由变分自编码器(VAE)、U-Net和一个文本编码器三个部分组成。在前向扩散过程中,高斯噪声被迭代地应用于压缩的潜在表征。每个去噪步骤都由一个包含残差神经网络(ResNet)的U-Net架构完成,通过从前向扩散往反方向去噪而获得潜在表征。最后,VAE解码器通过将表征转换回像素空间来生成输出图像。

Stable Diffusion的优点包括更高的稳定性、更快的训练速度以及更易于优化。通过引入一个新的稳定性系数,Stable Diffusion能够控制模型的稳定性,从而避免了Latent Diffusion中出现的不稳定性问题。同时,通过使用更小的batch size和更少的步骤,以及更少的参数和更简单的网络结构,Stable Diffusion提高了训练速度并使得模型更易于优化。
然而,Stable Diffusion也存在一些缺点。由于引入了稳定性系数,它可能会牺牲一些生成样本的多样性。此外,虽然Stable Diffusion的训练速度更快,但生成样本的速度可能会变慢。
Stable Diffusion工作原理:
Stable Diffusion模型的工作原理基于一个扩散过程,逐步从噪声中恢复出图像信息。在训练阶段,模型会学习如何逐步将噪声转化为真实的图像数据。而在生成阶段,模型则可以从随机噪声出发,通过反向的扩散过程,生成出与训练数据分布相似的图像。
这个扩散过程可以分为以下几个步骤:
- 初始化:给定一个原始数据集,例如图像、文本或其他类型的数据。
- 扩散过程:在扩散过程中,模型会将数据逐渐地向原始数据集的中心值靠近。这个过程可以通过一个称为“扩散器”的函数来表示。扩散器接收当前数据值和一个小噪声项,输出一个新的数据值。这个过程重复多次,直到数据值接近原始数据集的中心值。
- 生成新数据:在扩散过程结束后,模型会生成一个新的数据样本,这个样本具有与原始数据集相似的特征。
- 反向扩散过程:为了提高生成数据的质量,Stable Diffusion使用了反向扩散过程。这个过程与正向扩散过程类似,但使用的是一个不同的扩散器。反向扩散过程可以使生成的数据更接近原始数据集的分布。
- 重复和优化:为了提高生成数据的多样性和平衡性,可以对扩散过程进行多次重复,并使用不同的扩散器和噪声参数。
Stable Diffusion模型通过引入条件控制、特征嵌入等技巧,能够生成具有多样性和创意性的图像。这种模型不仅具有高度的灵活性,可以生成各种类型的图像,如人脸、物体等,而且生成的图像质量高,逼真度和细节表现力较好。
Stable Diffusion核心代码实现
基于Python 和常见机器学习库实现:
算法核心流程
计算相似度矩阵
使用欧氏距离计算数据点之间的相似度。
使用高斯核函数转换欧氏距离为相似度。
pairwise_dist = pairwise_distances(X, metric='euclidean') similarity_matrix = np.exp(-pairwise_dist ** 2)中心化相似度矩阵
对相似度矩阵进行中心化处理,使其行和列的平均值为0。
kernel_centerer = KernelCenterer() similarity_matrix_centered = kernel_centerer.fit_transform(similarity_matrix)扩散过程
初始化一个单位矩阵作为扩散矩阵。
多次迭代扩散过程,将信息从每个数据点扩散到其相邻的数据点。
diffusion_matrix = np.eye(X.shape[0]) for _ in range(n_steps): diffusion_matrix = (1 - alpha) * diffusion_matrix + alpha * np.dot(similarity_matrix_centered, diffusion_matrix)提取主要方向
计算扩散矩阵的特征值和特征向量。
根据特征值排序,选择前几个主要方向作为新的特征向量。
eigenvalues, eigenvectors = np.linalg.eigh(diffusion_matrix) idx = np.argsort(eigenvalues)[::-1] principal_directions = eigenvectors[:, idx]
核心完整代码:
class StableDiffusion:
def __init__(self, alpha=0.5, n_steps=10):
self.alpha = alpha
self.n_steps = n_steps
self.principal_directions = None
def fit(self, X):
# 计算相似度矩阵
pairwise_dist = pairwise_distances(X, metric='euclidean')
similarity_matrix = np.exp(-pairwise_dist ** 2)
# 中心化相似度矩阵
kernel_centerer = KernelCenterer()
similarity_matrix_centered = kernel_centerer.fit_transform(similarity_matrix)
# 扩散过程
diffusion_matrix = np.eye(X.shape[0])
for _ in range(self.n_steps):
diffusion_matrix = (1 - self.alpha) * diffusion_matrix + self.alpha * np.dot(similarity_matrix_centered, diffusion_matrix)
# 提取主要方向(特征向量)
eigenvalues, eigenvectors = np.linalg.eigh(diffusion_matrix)
# 根据特征值排序,选择前几个主要方向
idx = np.argsort(eigenvalues)[::-1]
self.principal_directions = eigenvectors[:, idx]
def transform(self, X, n_components):
if self.principal_directions is None:
raise ValueError("Model has not been fitted yet.")
return np.dot(X, self.principal_directions[:, :n_components])
def plot_eigenvalues(self):
if self.principal_directions is None:
raise ValueError("Model has not been fitted yet.")
eigenvalues, _ = np.linalg.eigh(np.dot(self.principal_directions.T, self.principal_directions))
plt.figure(figsize=(8, 6))
plt.plot(np.arange(1, len(eigenvalues) + 1), eigenvalues[::-1], marker='o', linestyle='-')
plt.xlabel('Principal Components')
plt.ylabel('Eigenvalues')
plt.title('Eigenvalues of Principal Components')
plt.grid(True)
plt.show()
Stable Diffusion模型的应用场景
图像生成与艺术创作:Stable Diffusion模型在图像生成和艺术创作方面有着出色的表现。它能够学习大量图像数据的统计规律,并利用这些规律生成具有多样性和真实感的图像。这为艺术家和设计师提供了全新的创作工具,使他们能够创造出具有独特风格的图像作品。
音乐视频生成:通过结合音频输入和视觉模型,Stable Diffusion可以生成与音乐节奏和情感相匹配的视觉效果和动画。这种技术可用于音乐创作、艺术表演或广告制作等领域,为观众带来更具动感和艺术性的视觉体验。
表情动画生成:利用图像输入作为条件,结合面部表情模型和图像处理技术,Stable Diffusion可以生成角色动画并赋予其真实感和表情丰富性。这对于游戏开发、电影制作和虚拟现实等领域具有重要意义,能够实现更逼真和个性化的角色动画效果。
社交网络与信息传播:Stable Diffusion可以通过利用已有用户的社交网络,将信息传播给更多潜在客户,实现广告和宣传的效果。同时,它也可以用于研究社交网络中的信息传播过程,预测某个信息在网络中的传播范围和效果。
疾病传播模拟:Stable Diffusion可以用于模拟和预测病毒或疾病在人群中的传播过程。通过分析人群之间的联系和互动,可以预测疾病的传播速度和范围,并采取相应的防控措施。
金融市场分析:在金融市场中,Stable Diffusion可以通过分析股票、外汇或加密货币市场中的价格和交易数据,预测市场的波动性和未来价格走势,帮助投资者做出更明智的投资决策。
城市规划与交通管理:Stable Diffusion还可以用于优化城市交通和人流管理。通过分析城市中的人口流动和交通网络,可以预测交通拥堵情况、优化交通路线和补充城市基础设施,从而提高城市运行效率与交通安全性。

Stable Diffusion免费使用网站
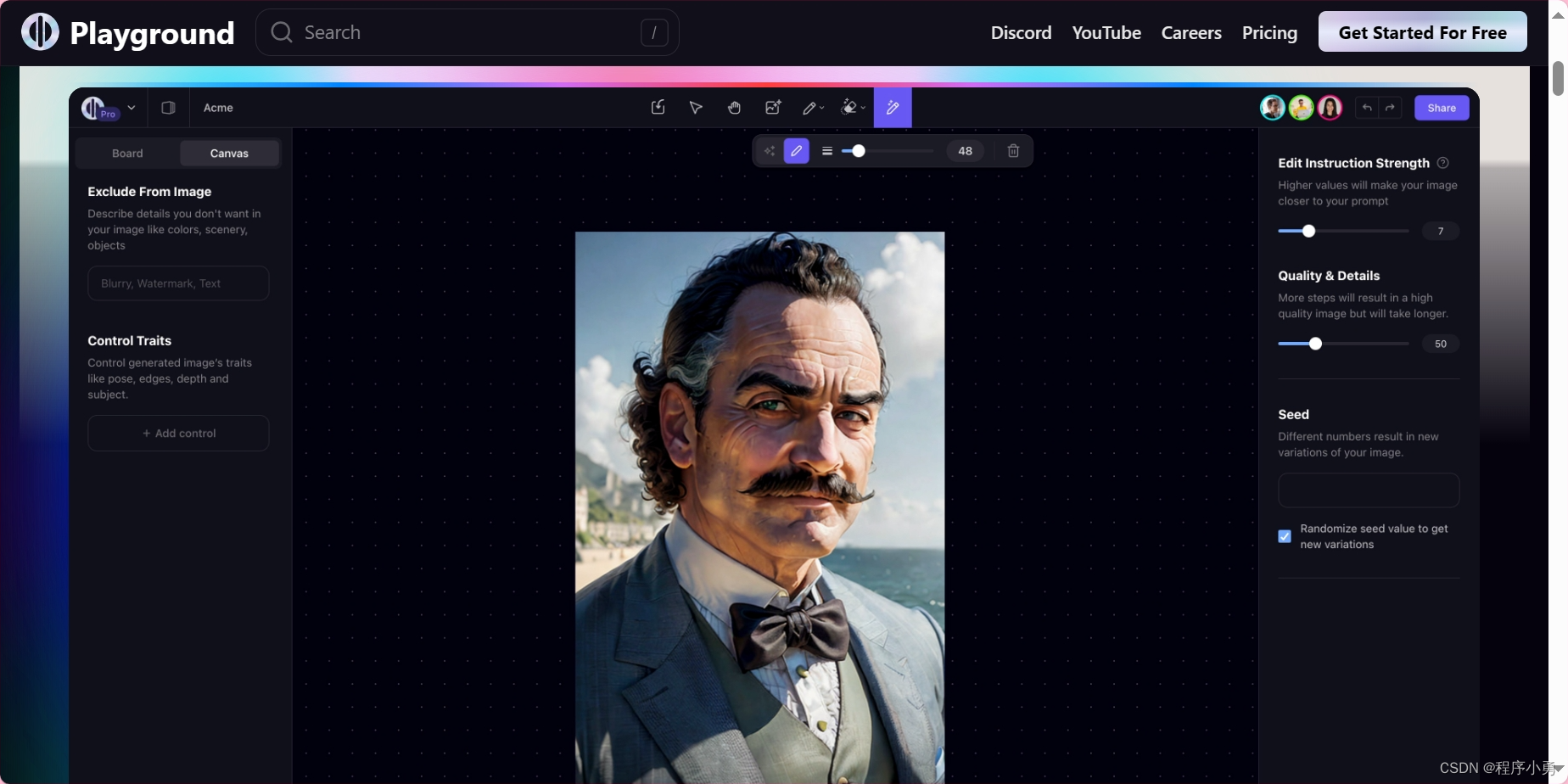
Playground AI:
这是一个创新的在线工具,特别适合用于创新设计。它允许用户生成人工智能驱动的图像,释放创意能力。提供无缝的方式来轻松创建社交媒体帖子、艺术品、演示文稿、视频、徽标和海报。
因其强大的图像编辑器和预先设计的模板、背景和效果库,用户可以个性化创作。
Fotor:
这是一个用户友好的AI图像生成器,利用AI功能生成具有视觉吸引力的设计和艺术品。
它可能提供了一系列工具和模板,帮助用户快速创建高质量的图像内容。

绘世整合包:
这是一个易于使用的整合包,集成了AI绘画的核心需求,如ControlNet插件和最新的深度学习技术。它为初学者和没有编程知识的人提供了从零开始学习使用Stable Diffusion的机会。
推荐B站的秋叶发布的【绘世整合包】作为软件本整合包基于开源项目Stable Diffusion WebUI制作

ComfyUI:这是一个基于节点操作的UI界面插件,适合显卡配置较低的用户。它优化了内部生成流程,提高了生成图片的速度,并提供了更自由的生成控制。
stability.ai:


本地部署 Stable Diffusion方法:
推荐网站:
StableDiffusion中文网
开源AI绘图工具Stable Diffusion中文资源站

总结
今天主要分享Stable Diffusion模型的简介,该模型是深度学习领域的一种革命性生成式模型,它通过模拟复杂的扩散过程,将随机噪声逐渐转化为具有高度细节和真实感的图像。这一模型的强大之处在于它能够从大量图像数据中学习到图像分布的内在规律,并通过优化算法生成出与训练数据相似但全新的图像。
今天内容分享到这里哦!