977 有序数组平方
看完题后的思路
双指针
思路
本题如果使用暴力解法,需要按照绝对值将数组排序0(logn),然后进行平方.(或先平方,再排序,这样可以直接调用排序函数) 可以使用双指针法,定义两个指针,左指针是当前绝对值最小的负数,右指针是当前绝对值最小的整数,每一轮将较小数的平方放入结果数组,指针向左或右移动一格.
代码
//977 有序数组平方
public int[] sortedSquares(int[] nums) {
int left=-1,right=nums.length; // left 当前待处理的负数 right 当前待处理的正数
int[] result = new int[nums.length];
// 先提前判断全正 全负的情况
if (nums[0]>=0){
right=0;
}
if (nums[nums.length-1]<0){
left=nums.length-1;
}
// 找到初始位置
for (int i = 0; i < nums.length; i++) {
if (nums[i]>=0){
left=i-1;
right=i;
break;
}
}
//核心逻辑
int i=0;
while (left>=0&&right<nums.length){
if (-1*nums[left]<nums[right]){
result[i++]=nums[left]*nums[left];
left--;
}else {
result[i++]=nums[right]*nums[right];
right++;
}
}
// 处理还没有到头的指针
while (left>=0){
result[i++]=nums[left]*nums[left];
left--;
}
while (right<nums.length){
result[i++]=nums[right]*nums[right];
right++;
}
return result;
}
复杂度
时间复杂度 0(n)
空间复杂度 0(n)
遇到的困难/进一步优化
- 代码中三个while有些冗余,能不能用一个while?
可以让left指向数组左端点,right指向数组右端点(从绝对值最大的方向遍历),终止条件为 left<right
978 有序数组平方
看完题后的思路
刚看完题,第一想到的肯定是暴力解法,毕竟双指针并不能一眼看出来,需要手动模拟+思考
思路
这道题首先想到的是暴力解法,两层for循环,时间复杂度为 0(n^2),使用滑动窗口能把时间复杂度降到0(n),这说明暴力解法一定有很多步骤是无用的,找到这些无用的步骤对我们理解双指针和重要
这是暴力的代码
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
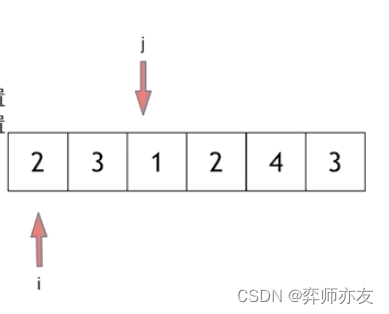
如果我们需要找到大于5的最短子数组,当循环到上面位置的时候,我们这道一个候选结果,此时j再向下循环是无意义的,因为此后的[i,j]和一定大于5,而且长度一定大于3.此时我们可以直接跳出本次循环,进行下一次i=1的循环来省去这些无用功
当进行下一层循环时,如果j从i开始,也会做一些无用功,如下图:

当将上面两种无用功避免之后,暴力算法就变成了滑动窗口算法.
代码 (滑动窗口模板)
//209 长度最小的子数组
public int minSubArrayLen(int target, int[] nums) {
int left=0,right=0; // 窗口左右边界 []
int sum=0;
int minLength=nums.length+1;
while (right<nums.length){
// 初始加入 和 某次循环加入
sum+=nums[right];
// 判断
while (sum>=target){
minLength=Math.min(minLength,right-left+1);
sum-=nums[left++];
}
// 此时 sum一定小于target
right++;
}
return minLength==nums.length+1 ? 0 : minLength;
}
复杂度
时间复杂度 0(n)
空间 复杂度0(1)
困难/进一步优化/收获
什么类型的题能使用滑动窗口?
窗口内的特征值(例如本题的和)是递增的,递增的意思是窗口收缩(左边界向前),特征值减小,窗口扩张,特征值变大.
59. 螺旋矩阵 II
看完题后的思路
二刷,温故知新
思路
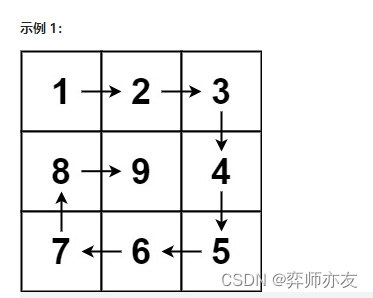
生成螺旋矩阵的过程可以看成一圈一圈生成的过程
代码
// 59. 螺旋矩阵 II
public int[][] generateMatrix(int n) {
int[][] res= new int[n][n];
int rount=0; // 轮数/圈数
int value=1; // 要赋予的值
while (rount<(n+1)/2){
int start=rount,end=n-rount-1; // 每轮开始位置 结束位置
// 上横
int mov=start; // 移动指针
while (mov<=end){
res[start][mov++]=value++;
}
//右竖
mov=start+1;
while (mov<=end){
res[mov++][end]=value++;
}
//下横
mov=end-1;
while (mov>=start){
res[end][mov--]=value++;
}
//左竖
mov=end-1;
while (mov>start ){
res[mov--][start]=value++;
}
rount++;
}
return res;
}
复杂度
时间复杂度 0(n^2)
空间 复杂度0(1)
困难/进一步优化/收获
无