动态规划Dynamic programming详解-编辑距离问题【python】

作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。
会一些的技术：数据分析、算法、SQL、大数据相关、python
欢迎加入社区：码上找工作
作者专栏每日更新：
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化：企业实战案例
备注说明：方便大家阅读，统一使用python，带必要注释，公众号数据分析螺丝钉一起打怪升级

动态规划是解决各种优化问题的强大工具，特别是在问题可以分解为重叠的子问题时。接下来，我将介绍一个流行的动态规划案例——编辑距离问题（又称Levenshtein距离）

1. 问题介绍和应用场景

编辑距离问题是一个经典的问题，用于量化两个字符串之间的差异，即将一个字符串转换成另一个字符串所需的最小编辑操作次数，包括插入、删除和替换字符。编辑距离广泛应用于自然语言处理、文本相似度检测、拼写检查、生物信息学等领域。

2. 问题定义和示例

定义：给定两个字符串 s1 和 s2，计算将 s1 转换成 s2 所需的最少操作数。

示例：

s1 = "horse"
s2 = "ros"

最少操作数为 3（删除 ‘h’，替换 ‘o’ 为 ‘r’，删除 ‘e’）。
在编辑距离问题中，状态转移方程是用来描述如何从较小问题的解构建较大问题的解的数学表达式。它核心地指示了在动态规划表中如何更新每个单元格的值。以下是详细的推导和解释。

3.状态转移方程

状态定义

设 dp[i][j] 为从字符串 s1 的前 i 个字符转换到 s2 的前 j 个字符所需的最小编辑操作数。这里，s1[0..i-1] 和 s2[0..j-1] 分别表示字符串 s1 和 s2 的前 i 和 j 个字符。

状态转移方程的推导

考虑以下几种情况：

字符匹配（s1[i-1] == s2[j-1]）:
- 如果当前两个字符相同，那么这一对字符不需要任何编辑操作。因此，当前问题的解可以直接继承前一个问题的解，即：
  [ dp[i][j] = dp[i-1][j-1] ]
- 这表示我们不对这对字符进行任何编辑，直接继承左上角单元格的编辑操作数。
字符不匹配（s1[i-1] != s2[j-1]）:
- 如果当前两个字符不相同，我们有三种策略来使得 s1[0..i-1] 转换为 s2[0..j-1]：
  - 删除操作：从 s1 中删除一个字符后，尝试匹配 s1[0..i-2] 至 s2[0..j-1]，操作数为 dp[i-1][j] + 1。
  - 插入操作：向 s1 中插入一个与 s2[j-1] 相同的字符，然后尝试匹配 s1[0..i-1] 至 s2[0..j-2]，操作数为 dp[i][j-1] + 1。
  - 替换操作：将 s1[i-1] 替换为与 s2[j-1] 相同的字符，然后匹配 s1[0..i-2] 至 s2[0..j-2]，操作数为 dp[i-1][j-1] + 1。
- 综上，我们选择上述三种策略中的最小值：
  [ dp[i][j] = 1 + \min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) ]

完整的状态转移方程

综合以上情况，编辑距离问题的状态转移方程可以表达为：

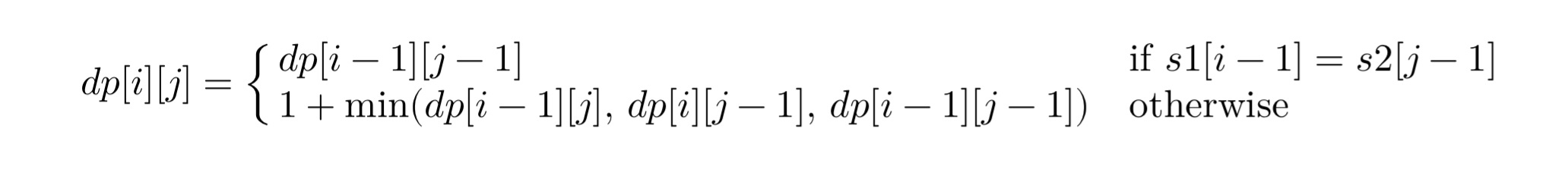
在这里插入图片描述

边界条件

对于 i = 0 (即 s1 为空字符串时)，将 s2 的前 j 个字符全部插入到 s1 是唯一的选项，因此 dp[0][j] = j。
对于 j = 0 (即 s2 为空字符串时)，将 s1 的前 i 个字符全部删除是唯一的选项，因此 dp[i][0] = i。

通过上述状态转移方程，我们可以系统地填充整个动态规划表，并最终解决编辑距离问题。这种方法不仅确保了解的正确性，而且通过避免冗余计算，提高了

4. 算法实现

def edit_distance(s1: str, s2: str) -> int:
    """
    计算两个字符串s1和s2之间的最小编辑距离。
    最小编辑距离是将s1转换成s2所需的最少单字符编辑操作次数（插入、删除、替换）。

    参数:
    s1 (str): 源字符串。
    s2 (str): 目标字符串。

    返回:
    int: s1转换成s2的最小编辑距离。
    """
    m, n = len(s1), len(s2)
    # 创建一个二维数组dp，大小为(m+1)x(n+1)
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    # 初始化dp数组的第一行和第一列
    for i in range(m + 1):
        dp[i][0] = i  # 将s1的前i个字符删除
    for j in range(n + 1):
        dp[0][j] = j  # 将s2的前j个字符插入到s1中

    # 填充dp数组的其余部分
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if s1[i - 1] == s2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]  # 字符相同，无需编辑
            else:
                dp[i][j] = 1 + min(dp[i - 1][j],    # 删除操作
                                   dp[i][j - 1],    # 插入操作
                                   dp[i - 1][j - 1])  # 替换操作

    return dp[m][n]  # 返回将整个s1转换成s2的最小编辑距离

# 示例使用
s1 = "horse"
s2 = "ros"
print("最小编辑距离:", edit_distance(s1, s2))

复杂度分析

时间复杂度：O(mn)，因为需要填充一个 m x n 的矩阵。
空间复杂度：O(mn)，可以优化到 O(min(m, n)) 通过只保留当前和前一行的状态。
为了清晰地解释编辑距离问题的动态规划解法，并辅以图解，我们可以使用一个示例和配套的表格。我们将采用简单的字符串 s1 = "horse" 和 s2 = "ros" 来阐述过程。

算法图解

动态规划表初始化

创建一个表格，其中行表示字符串 s1 的前 i 个字符，列表示字符串 s2 的前 j 个字符。我们使用一个 (len(s1)+1) x (len(s2)+1) 的表格，len(s1) 和 len(s2) 分别是两个字符串的长度。

初始化表格（第一行和第一列特殊处理）

初始表格结构如下：

		R	O	S
	0	1	2	3
H	1
O	2
R	3
S	4
E	5

第一行 和 第一列 的填充是基于单字符插入和删除操作的累积成本。例如，第一行第二格的 1 表示将空串变为 “R” 需要一次插入操作，依此类推。

填充过程

遍历 s1 的每个字符（行），与 s2 的每个字符（列）进行比较：

H vs R:
- 不匹配。取 min(左方, 上方, 左上方+1) → min(1, 1, 1) = 1 (dp[1][1] 表示从"H"到"R"的最小编辑距离)
H vs O:
- 不匹配。min(1, 2, 2) = 2 (由 “H” 到 “RO” 或由 “HO” 到 “R”)
H vs S:
- 不匹配。min(2, 3, 3) = 3 (由 “H” 到 “ROS” 或由 “HS” 到 “RO”)
O vs R:
- 不匹配。min(2, 1, 2) = 2 (由 “O” 到 “R” 或由 “HO” 到 “RO”)
O vs O:
- 匹配。dp[1][1] + 0 = 1 (无操作, 因为 “O” 匹配 “O”)
O vs S:
- 不匹配。min(3, 2, 2) = 2 (由 “O” 到 “ROS” 或由 “HO” 到 “OS”)
R vs R:
- 匹配。dp[2][1] + 0 = 2 (无操作, 因为 “R” 匹配 “R”)
R vs O:
- 不匹配。min(2, 3, 3) = 3 (由 “HR” 到 “RO” 或由 “HOR” 到 “R”)
R vs S:
- 不匹配。min(3, 4, 3) = 3 (由 “HR” 到 “ROS” 或由 “HOR” 到 “OS”)
Final Row (E):
- 类似上述步骤，我们继续用 s1 的 “E” 与 s2 的每个字符进行比较填表。

继续填充表格的详细步骤：

		R	O	S
	0	1	2	3
H	1	1	2	3
O	2	2	1	2
R	3	2	2	2
S	4	3	3	2
E	5	4	4	3

逐步分析与填充

S vs R, O, S:
- S vs R: 不匹配。min(左方, 上方, 左上方+1) → min(3, 2, 3) = 2
- S vs O: 不匹配。min(左方, 上方, 左上方+1) → min(2, 3, 3) = 2
- S vs S: 匹配。dp[4][3] → dp[3][2] + 0 = 2
E vs R, O, S:
- E vs R: 不匹配。min(左方, 上方, 左上方+1) → min(4, 3, 3) = 3
- E vs O: 不匹配。min(左方, 上方, 左上方+1) → min(3, 4, 4) = 3
- E vs S: 不匹配。min(左方, 上方, 左上方+1) → min(2, 3, 4) = 2

完整填充后的表格

		R	O	S
	0	1	2	3
H	1	1	2	3
O	2	2	1	2
R	3	2	2	2
S	4	3	3	2
E	5	4	4	3

在最右下角的单元格 dp[5][3]，我们得到 s1 = "horse" 和 s2 = "ros" 的最小编辑距离为 3。这表明我们需要进行三次编辑操作（删除两个字符 ‘h’ 和 ‘e’，并将一个 ‘r’ 替换为 ‘o’）来将 “horse”
回溯过程转换成 “ros”。以下是更加具体的步骤和解释：

回溯过程

要详细了解如何从 “horse” 变成 “ros”，我们可以从填充完成的动态规划表格开始回溯。从表格的右下角 (dp[5][3]) 开始，每一步都选择了一个操作，直到我们回到表格的左上角 (dp[0][0])。

从表格回溯操作：

从 ‘e’ 到 ‘s’：
- 位置 (5, 3): 此时字符 ‘e’ (s1的第5个字符) 和 ‘s’ (s2的第3个字符) 不匹配。
- 可以通过将 ‘e’ 替换为 ‘s’ 来减少一个不匹配，即 dp[4][2]。所以我们进行替换操作。
从 ‘s’ 到 ‘s’：
- 位置 (4, 2): 此时字符 ‘s’ 和 ‘s’ 匹配。
- 由于字符匹配，我们直接沿对角线向上移动到 dp[3][1]，无需额外操作。
从 ‘r’ 到 ‘o’：
- 位置 (3, 1): 此时字符 ‘r’ 和 ‘o’ 不匹配。
- 可以通过将 ‘r’ 替换为 ‘o’ 来减少一个不匹配，即 dp[2][0]。所以我们进行替换操作。
从 ‘o’ 到 ‘’ (空)：
- 位置 (2, 0): 此时我们需要将 ‘o’ 删除，因为s2已无更多字符。
- 沿着第一列向上，每次删除 s1 中的字符，直到 dp[1][0]。
从 ‘h’ 到 ‘’ (空)：
- 位置 (1, 0): 最后，删除 ‘h’，完成所有转换。