今天的题又简单了很多欸
1.简写单词
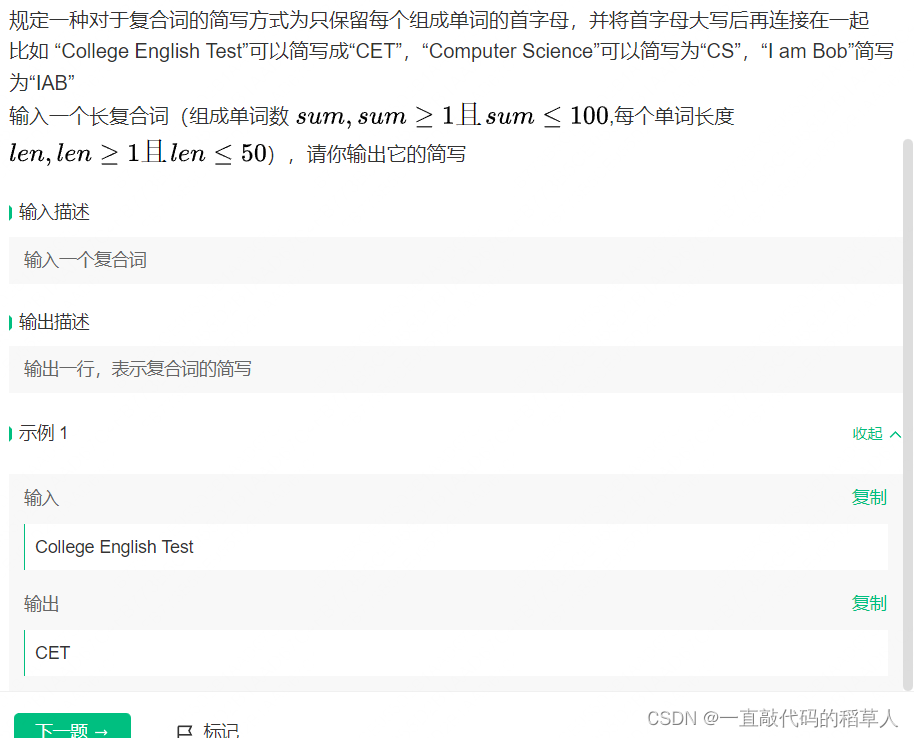
没思路
代码:
#include <iostream>
#include<string>
using namespace std;
int main() {
string str;
string ans;
getline(cin,str);
if(str[0]>'Z')ans+=(str[0]-32);
else ans+=str[0];
for(int i=1;i<str.size();i++){
if(str[i]!=' '&&str[i-1]==' '){
if(str[i]>'Z')ans+=(str[i]-32);
else ans+=str[i];
}
}
cout<<ans;
return 0;
}
2.dd爱框框
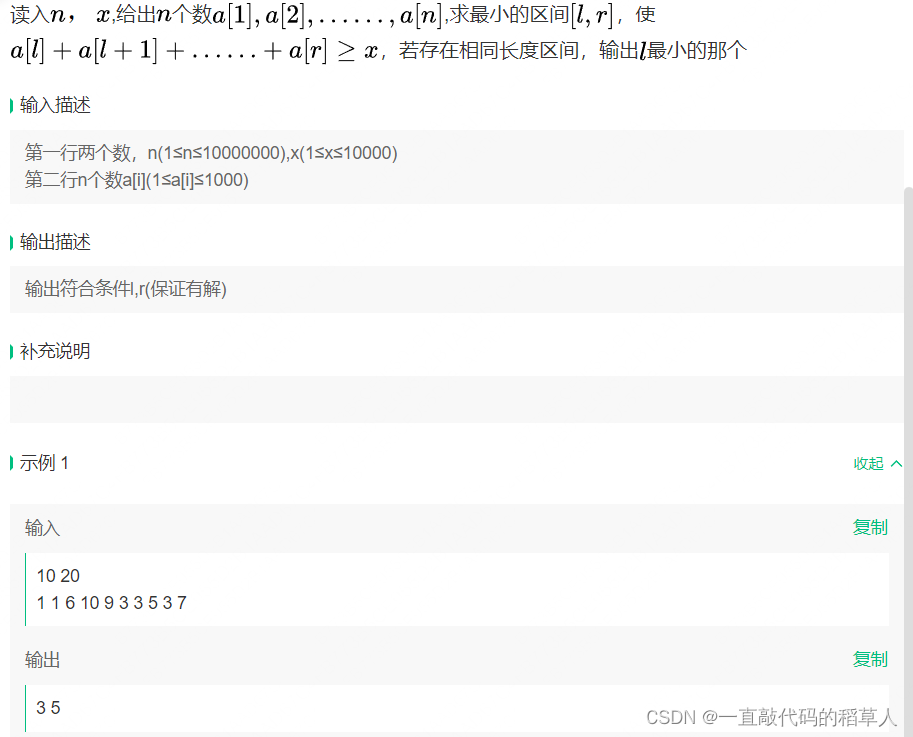
思路:
先维护一个前缀和s[].遍历每一个区间的左端点,去看看要想大于等于x 的最近右端点在哪。
由于区间和(正数)是具有单调性,这里可以用二分。对于每个可能的左端点,都二分查找一个符合条件的最近右端点。 这样我们就能把所有符合答案的情况求出来了,再用一个变量维护最小长度,这个长度最终是所有可能符合答案中的最小值。
注意题目要求输出答案区间,所以我们还需要维护一个左端点就行了,左端点加上答案长度就是答案的右端点。
写完之后发现双指针就可以了草。用两个指针维护一个区间的左右端点嘛,如果当前区间和小于x,那就右端点移动。否则左端点移动,缩小答案区间。
二分代码:
#include <iostream>
using namespace std;
typedef long long ll;
const int N=1e7+10;
ll s[N];
int main() {
int n;
int x;
cin>>n>>x;
for(int i=1;i<=n;i++){
int k;
cin>>k;
s[i]=s[i-1]+k;
}
int ans=1e9;
int star=1;
for(int i=1;i<=n;i++){
int l=i-1;
int r=n+1;
while(l+1!=r){
int mid=(l+r)>>1;
if(s[mid]-s[i-1]>=x)r=mid;//符合条件放在右边,最后右边的第一个就是最小的右端点
else l=mid;
}
if(s[r]-s[i-1]>=x){
if(r-i+1<ans){
ans=r-i+1;
star=i;
}
}
}
cout<<star<<" "<<star+ans-1;
return 0;
}双指针代码:
#include <iostream>
using namespace std;
typedef long long ll;
const int N=1e7+10;
int a[N];
int main() {
int n;
int x;
cin>>n>>x;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int ans=1e9;
int star=1;
ll sum=0;
for(int i=1,j=1;i<=n;i++){
sum+=a[i];
while(sum>=x){
if(i-j+1<ans){
ans=i-j+1;
star=j;
}
sum-=a[j];
j++;
}
}
cout<<star<<" "<<star+ans-1;
return 0;
}3.除2!

思路:
一眼看上去k很大,吓得我以为不能暴力了00
后来发现,一个int最大是2^32,即使这n个数都是一个最大的偶数,一共也最多被操作32*1e5
所以直接暴力枚举每次操作就行了。每次操作对最大的数除2,这样贡献才越大。用优先队列维护一下就行。
代码:
#include <iostream>
#include<queue>
using namespace std;
int main() {
int n,k;
cin>>n>>k;
long long sum=0;//存总和
priority_queue<int> q;
while(n--){
int x;
cin>>x;
sum+=x;
if(x%2==0)q.push(x);//不是偶数直接滚
}
while(!q.empty()&&k){
int it=q.top();
q.pop();
it/=2;
sum-=it;
k--;
if(it%2==0)q.push(it);//不是偶数也没有再进去的必要了
}
cout<<sum;
return 0;
}