1. AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

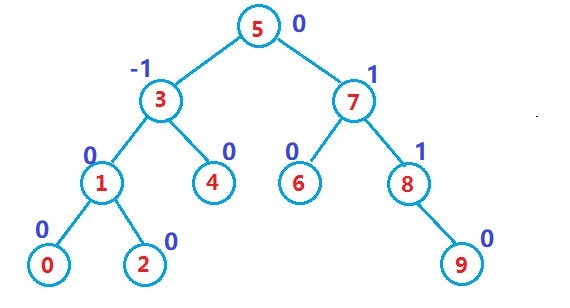
一棵AVL树要么是空树，要么是具有以下性质的二叉搜索树：

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 $O(log_2 n)$ ，搜索时间复杂度O( $log_2 n$ )

2. AVL树节点的定义

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	// 高度差：右子树-左子树
	int _bf;// balance factor

	AVLTreeNode(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

3. AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。

那么AVL树的插入过程可以分为两步：

按照二叉搜索树的方式插入新节点
调整节点的平衡因子

//按搜索二叉树规则插入
//更新平衡因子，旋转使其平衡
bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (kv.first > cur->_kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (kv.first < cur->_kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
            return false;
    }

    cur = new Node(kv);
    if (kv.first > parent->_kv.first)
    {
        parent->_right = cur;
    }
    else
    {
        parent->_left = cur;
    }
    cur->_parent = parent;

    //更新平衡因子
    while (parent)//最深要更新到根
    {
        if (cur == parent->_left)
        {
            parent->_bf--;
        }
        else
        {
            parent->_bf++;
        }

        //是否继续更新
        if (0 == parent->_bf)//两边平衡了
        {
            break;
        }
        else if (1 == parent->_bf || -1 == parent->_bf)// 子树的高度变了，继续更新祖先
        {
            cur = parent;
            parent = parent->_parent;
        }
        else if (2 == parent->_bf || -2 == parent->_bf)
        {
            //子树不平衡，需要旋转处理
            if (parent->_bf == 2 && cur->_bf == 1)//左单旋
            {
                RotateL(parent);
            }
            else if (parent->_bf == -2 && cur->_bf == -1)//右单旋
            {
                RotateR(parent);
            }
            else if (parent->_bf == -2 && cur->_bf == 1)
            {
                RotateLR(parent);
            }
            else if (parent->_bf == 2 && cur->_bf == -1)
            {
                RotateRL(parent);
            }

            break;
        }
        else
        {
            // 插入之前AVL就存在不平衡子树，就有>=2的平衡因子出现，之前的程序有问题
            assert(false);
        }
    }
    return true;
}

4. AVL树的旋转

如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

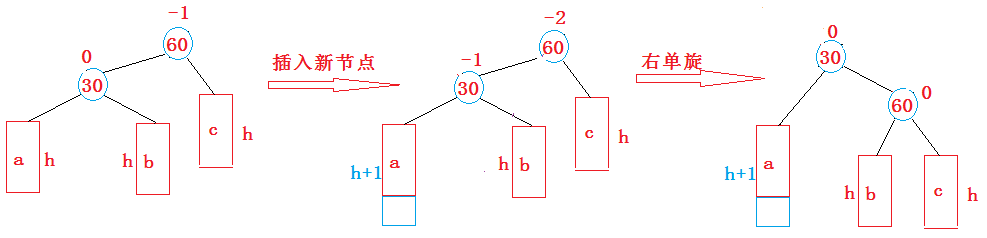
新节点插入较高左子树的左侧—左左：右单旋

/*
上图在插入前，AVL树是平衡的，新节点插入到30的左子树(注意：此处不是左孩子)中，30左子树增加了一层，导致以60为根的二叉树不平衡，要让60平衡，只能将60左子树的高度减少一层，右子树增加一层，即将左子树往上提，这样60转下来，因为60比30大，只能将其放在30的右子树，而如果30有右子树，右子树根的值一定大于30，小于60，只能将其放在60的左子树，旋转完成后，更新节点的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：
1. 30节点的右孩子可能存在，也可能不存在
2. 60可能是根节点，也可能是子树
如果是根节点，旋转完成后，要更新根节点
如果是子树，可能是某个节点的左子树，也可能是右子树
*/
void _RotateR(PNode pParent)
{
    // pSubL: pParent的左孩子
    // pSubLR: pParent左孩子的右孩子，注意：该
    PNode pSubL = pParent->_pLeft;
    PNode pSubLR = pSubL->_pRight;
    // 旋转完成之后，30的右孩子作为双亲的左孩子
    pParent->_pLeft = pSubLR;
    // 如果30的左孩子的右孩子存在，更新亲双亲
    if(pSubLR)
    	pSubLR->_pParent = pParent;
    // 60 作为 30的右孩子
    pSubL->_pRight = pParent;
    // 因为60可能是棵子树，因此在更新其双亲前必须先保存60的双亲
    PNode pPParent = pParent->_pParent;
    // 更新60的双亲
    pParent->_pParent = pSubL;
    // 更新30的双亲
    pSubL->_pParent = pPParent;
    // 如果60是根节点，根新指向根节点的指针
    if(NULL == pPParent)
    {
        _pRoot = pSubL;
        pSubL->_pParent = NULL;
    }
    else
    {
        // 如果60是子树，可能是其双亲的左子树，也可能是右子树
        if(pPParent->_pLeft == pParent)
            pPParent->_pLeft = pSubL;
        else
            pPParent->_pRight = pSubL;
    }
    // 根据调整后的结构更新部分节点的平衡因子
    pParent->_bf = pSubL->_bf = 0;
}

新节点插入较高右子树的右侧—右右：左单旋

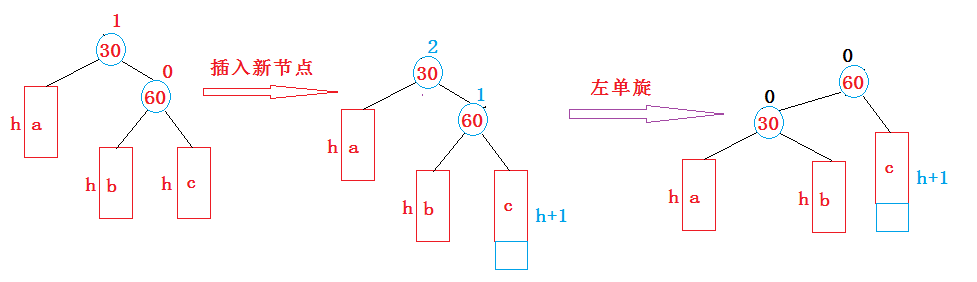
新节点插入较高左子树的右侧—左右：先左单旋再右单旋

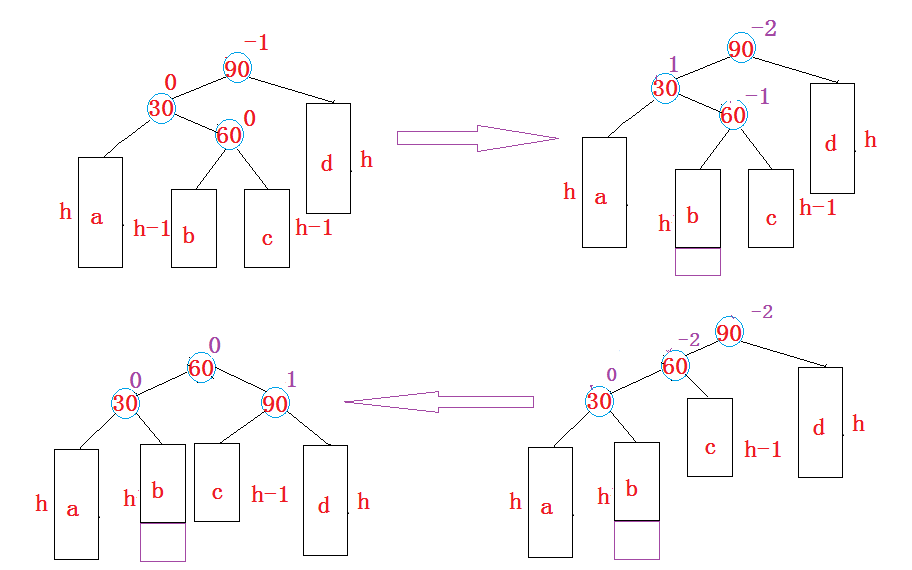
将双旋变成单旋后再旋转，即：先对30进行左单旋，然后再对90进行右单旋，旋转完成后再考虑平衡因子的更新。

// 旋转之前，60的平衡因子可能是-1/0/1，旋转完成之后，根据情况对其他节点的平衡因子进行调整
void _RotateLR(PNode pParent)
{
    PNode pSubL = pParent->_pLeft;
    PNode pSubLR = pSubL->_pRight;
    // 旋转之前，保存pSubLR的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节点的平衡因子
    int bf = pSubLR->_bf;
    // 先对30进行左单旋
    _RotateL(pParent->_pLeft);
    // 再对90进行右单旋
    _RotateR(pParent);
    if(1 == bf)
    	pSubL->_bf = -1;
    else if(-1 == bf)
    	pParent->_bf = 1;
}

新节点插入较高右子树的左侧—右左：先右单旋再左单旋

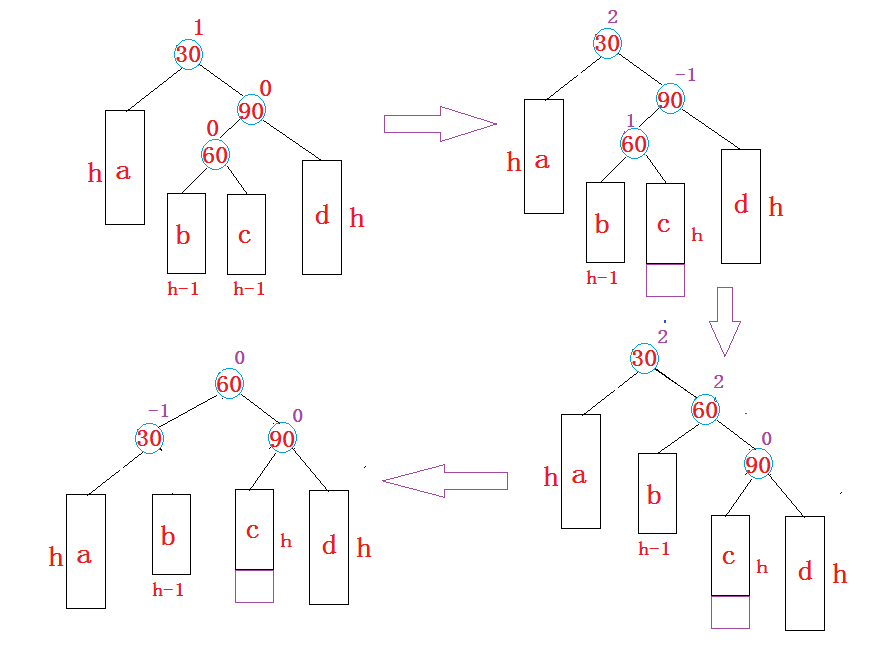
总结：
假如以pParent为根的子树不平衡，即pParent的平衡因子为2或者-2，分以下情况考虑

pParent的平衡因子为2，说明pParent的右子树高，设pParent的右子树的根为pSubR
当pSubR的平衡因子为1时，执行左单旋
当pSubR的平衡因子为-1时，执行右左双旋
pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL
当pSubL的平衡因子为-1是，执行右单旋
当pSubL的平衡因子为1时，执行左右双旋

旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。

5. AVL树的验证

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

验证其为二叉搜索树
如果中序遍历可得到一个有序的序列，就说明为二叉搜索树
验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
节点的平衡因子是否计算正确

bool _IsBalanceTree(Node* root)
{
    if (root == nullptr)
        return true;

    int leftHeight = _Height(root->_left);
    int rightHeight = _Height(root->_right);
    int diff = rightHeight - leftHeight;

    if (abs(diff) >= 2)
    {
        cout << root->_kv.first << "不平衡咯" << endl;
        return false;
    }
    if (diff != root->_bf)
    {
        cout << "这都能算错？快去检测" << endl;
        return false;
    }

    return _IsBalanceTree(root->_left)
        && _IsBalanceTree(root->_right);
}

6. AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即 $log_2 (N)$ 。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。