今日任务:
1)343. 整数拆分
2)96.不同的二叉搜索树
3)复习day11
343. 整数拆分
题目链接:343. 整数拆分 - 力扣(LeetCode)
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。 示例 1: 输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2: 输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 说明: 你可以假设 n 不小于 2 且不大于 58。
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分哔哩哔哩bilibili
思路:
1. 创建一个一维数组
dp,其中dp[i]表示将正整数i拆分后得到的最大乘积。2. 初始时,将
dp[0]和dp[1]都设为0,因为0和1无法拆分成至少两个正整数的和。3. 对于正整数
i,从1开始遍历到i-1,对每个位置j,计算将i拆分成j和i-j的和,然后将这两部分的最大乘积相乘得到当前的最大乘积。4. 在计算
dp[i]时,需要考虑i-j是否继续拆分,如果i-j继续拆分后的最大乘积大于i-j本身,那么就可以继续拆分,否则不拆分。5. 最后返回
dp[n],即正整数n拆分后得到的最大乘积。
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] * (n + 1)
dp[2] = 1 # 2只能拆分为1+1,所以初始为1
for i in range(3, n + 1):
for j in range(1, (i+1)//2+1):
# 将i拆分成j和i-j,比较i-j的拆分结果与i-j本身的乘积,取最大值
dp[i] = max(dp[i], max(j * dp[i - j], j * (i - j)))
return dp[n]第二层for循环时,最初的想法从1遍历到i-1,去拆分。但实际上,由于对称性,只需要遍历到i的一半就足够了。这样做可以减少不必要的计算,提高代码效率。
刚才的思路是动态规划,这题我们还可以找寻数学规律去做
- 首先考虑特殊情况,当n为2时,最大乘积为1;当n为3时,最大乘积为2。
- 对于其他大于3的n,尽可能多地拆分成3,并计算拆分后的乘积。
- 根据数学规律,当n为3的倍数时,将n全部拆分为3可以得到最大乘积。
- 当n除以3余数为1时,将最后一个3拆分为2*2可以得到更大的乘积。
- 当n除以3余数为2时,直接拆分为3的乘积即可。
class Solution:
def integerBreak(self, n: int) -> int:
# 如果n为2,只能拆分为1+1,所以乘积为1
if n == 2:
return 1
# 如果n为3,只能拆分为1+2,所以乘积为2
if n == 3:
return 2
# 如果n可以被3整除,全部拆分为3的乘积会得到最大值
if n % 3 == 0:
return 3 ** (n // 3)
# 如果n除以3余数为1,那么将最后的3拆分为2*2可以得到更大的乘积
if n % 3 == 1:
return 3 ** ((n - 4) // 3) * 4
# 如果n除以3余数为2,直接拆分为3的乘积
if n % 3 == 2:
return 3 ** (n // 3) * 296.不同的二叉搜索树
题目链接:96. 不同的二叉搜索树 - 力扣(LeetCode)
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种? 示例 1: 输入:n = 3 输出:5 解析:[1,None,3,2,None],[1,None,2,None,3],[2,1,3],[3,2,None,1,None],[3,1,None,,None,2] 示例 2: 输入:n = 1 输出:1
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划找到子状态之间的关系很重要!| LeetCode:96.不同的二叉搜索树哔哩哔哩bilibili
思路:
这个问题可以通过动态规划来解决。我们可以定义一个数组
dp,其中dp[i]表示以1 ... i为节点组成的二叉搜索树的数量。然后,我们可以通过迭代计算dp[i]的值,直到dp[n]为止。1. 当
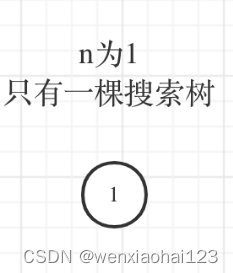
n = 0或n = 1时,只有一种情况,即空树或只有一个节点的树,此时dp[0] = dp[1] = 1。
2. 对于任意
i,我们可以将2... i中的每个数字都作为根节点,然后分别计算左子树和右子树的数量,最后将左右子树的数量相乘即可得到以i为根节点的二叉搜索树的数量。这个过程可以表示为dp[i] = sum(dp[j - 1] * dp[i - j]),其中j表示根节点的值。
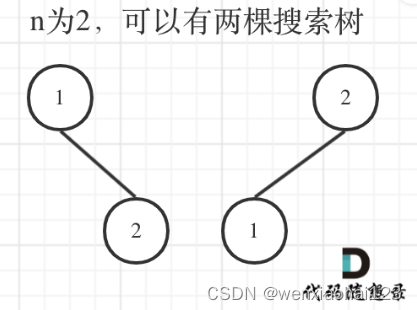
- 当n = 2 有两个节点时:
- 我们以1为根节点时,其左子树没有节点,故左子树只有一种情况,那就是空,右子树只有一个节点,那就是n=1的情况故为1。组合起来有1*1=1种情况
- 我们以2为根节点时,其左子树只有一个节点,那就是n=1的情况故为1,右子树没有节点故为空一种情况。组合起来有1*1=1种情况
- 故合起来n = 2 有两个节点时有1+1=2两种情况
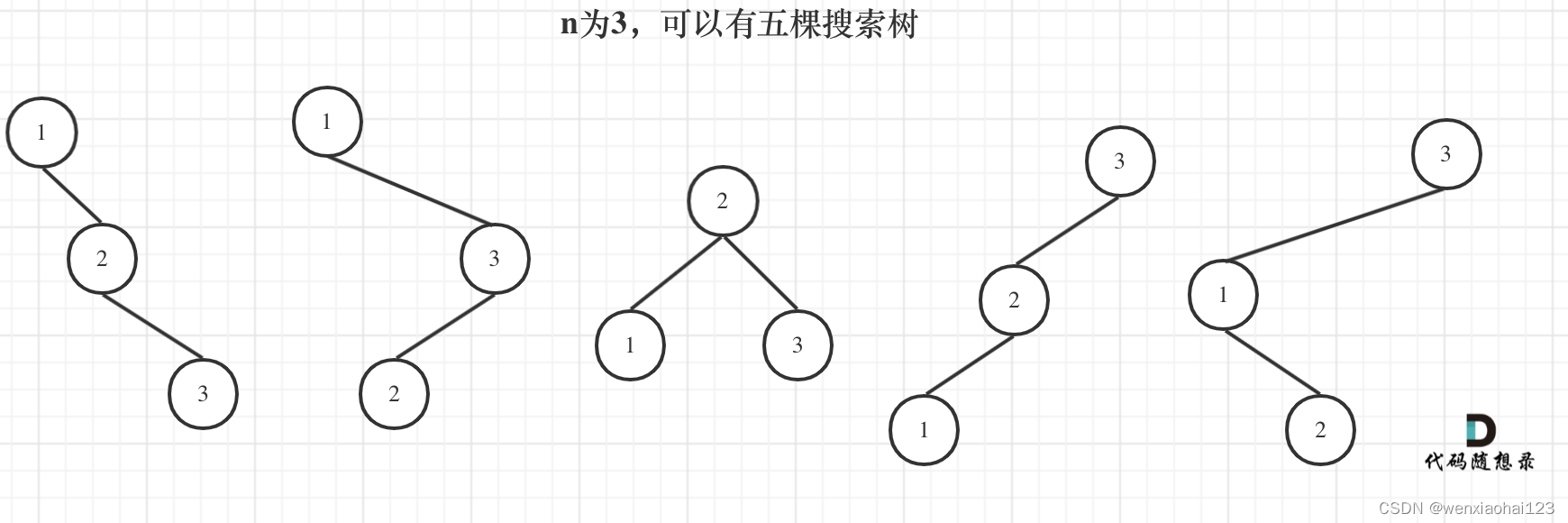
- 当n = 3 有三个节点时:
- 我们以1为根节点时,其左子树没有节点故为空1种情况,右子树只有两个节点,那就是n=2的情况故为2。组合起来有1*2=2种情况
- 我们以2为根节点时,其左右子树只有一个节点,那就是n=1的情况故为1,组合起来有1*1=1种情况
- 我们以3为根节点时,其左子树只有两个节点,那就是n=2的情况故为2,右子树没有节点故为空1种情况
- 合起来n = 2 有两个节点时有2+1+2=5两种情况
3.最终返回
dp[n]即可。
class Solution:
def numTrees(self, n: int) -> int:
# 初始化动态规划数组,dp[i] 表示以 1 ... i 为节点组成的二叉搜索树的数量
dp = [0] * (n + 1)
dp[0]= 1
for i in range(1, n + 1):
for j in range(i):
dp[i] += dp[j] * dp[i - j - 1]
return dp[n]