算法设计与分析实验报告c++实现(矩阵链相乘、投资问题、完全背包问题、数字三角形、最小生成树、背包问题)

news2024/11/27 0:23:21

一、实验目的

1．加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握；
2．提高学生利用课堂所学知识解决实际问题的能力；
3．提高学生综合应用所学知识解决实际问题的能力。

二、实验任务

用动态规划算法实现：

1、矩阵链相乘问题

image-20240403221859941

2、投资问题

image-20240403221853588

3、求解完全背包问题

问题描述：有n种重量和价值分别为wi、vi（1≤i≤n）的物品，从这些物品中挑选总重量不超过W的物品，求出挑选物品价值总和最大的挑选方案，这里每种物品可以挑选任意多件。4、数字三角形
问题描述：在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。

4、数字三角形

问题描述：在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。

image-20240403221846682

用贪心算法实现：

5、最小生成树问题（Prim算法和Kruskal算法）

设G=(V，E)是一个无向连通网，生成树上各边的权值之和称为该生成树的代价，在G的所有生成树中，代价最小的生成树称为最小生成树（Minimal Spanning Trees）。

6、背包问题
【问题描述】设有编号为1、2、…、n的n个物品，它们的重量分别为w1、w2、…、wn，价值分别为v1、v2、…、vn，其中wi、vi（1≤i≤n）均为正数。
有一个背包可以携带的最大重量不超过W。求解目标：在不超过背包负重的前提下，使背包装入的总价值最大（即效益最大化），与0/1背包问题的区别是，这里的每个物品可以取一部分装入背包。

三、实验设备及编程开发工具

实验设备：惠普Win10电脑
开发工具：Java和python环境下，eclipse和pycharm编程工具

四、实验过程设计（算法思路及描述，代码设计）

一．矩阵相乘问题

基本原理和思路：
1、动态规划的第一步：寻找最优子结构。为方便起见，使用Ai…j表示AiAi+1…Aj的乘积结果矩阵。对于k(i<=k<j), 计算Ai…j所需要的计算量为：Ai…k 和 Ak+1…j 以及二者相乘的代价和。
2、设m[i][j]为Ai…j的最优计算顺序所要花费的代价。则其求解公式为：
if i == j, m[i][j] = 0; //因为只有一个矩阵时计算代码为0，即不需要计算。
m[i][j]=min{m[i][k] + m[k+1][j] + Pi-1PkPj} i<=k<j
3、为了能够输出求解顺序，需要保存区间中的一些分割点。假如Ai…j中的最优分割点为k，则我们使用s[i][j]=k。即在Ai…j中，分别计算Ai…k 和 Ak+1…j 所用的计算开销最小。
4、采用自底向上的表格法。依次求解矩阵长度为2,3,…,n的最优计算顺序。

代码实现如下：

#include <stdio.h>
int m[1002][1002],s[1002][1002];
void matrix_chain(int a[], int n)
{
	int l, i, j, k, tmp;
	for(l=2; l<=n; l++)
	{
		for(i=1; i<=n-l+1; i++)		//长度为l的区间，其最小下标为1～n-l+1
		{
			j=i+l-1;
			m[i][j] = 0x7fffffff;
			for(k=i; k<j; k++)		//i~k, k+1~j, 所以k<j
			{
				tmp = m[i][k]+m[k+1][j]+a[i-1]*a[k]*a[j];
				if(tmp < m[i][j])
				{
					m[i][j] = tmp;
					s[i][j] = k;
				}
			}
		}
	}

}
void print(int i, int j)
{
	if(i == j)
		printf("A%d",i);
	else{
		printf("(");
		print(i, s[i][j]);
		print(s[i][j]+1, j);
		printf(")");
	}
}
int main()
{
	int n, a[1002];
	int i,j,l;
	while(scanf("%d",&n)==1)	//输入有n个矩阵
	{
		for(i=0; i<n+1; i++)
			scanf("%d",&a[i]);
		
		//memset(m, 0x7fffffff,sizeof(m));
		for(i=0; i<n+1; i++)
			m[i][i] = 0;
		matrix_chain(a, n);
		printf("%d\n",m[1][n]);
		print(1, n);
		printf("\n");
	}

	return 0;
}

img

分析：时间复杂度为O(N3)， 我们只需要存储一个矩阵就可以了，所以空间复杂度是 O(N2)。

二．投资问题

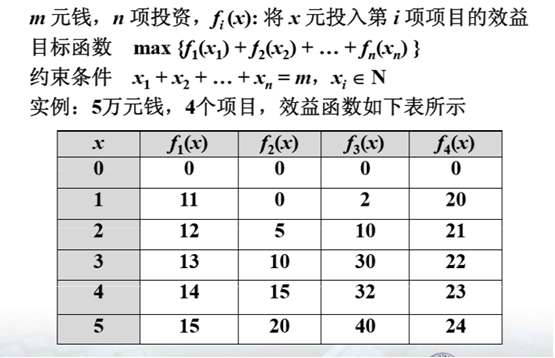
基本原理和思路：假设分配给第 i 个项目的钱数是 xi，问题描述为：
目标函数：max{f1(x1)+f2(x2)+…+fn(xn)}
约束条件：x1+x2+…+xn=m,xi∈N；设Fk(x)表示x元投给前k个项目的最大效益，k=1,2,…,n，x=1,2,…,m递推方程：Fk(x)=max{fk(xk)+Fk-1(x-xk)}(0≤xk≤x)，k=2,3,…,n边界条件：F1(x)=f1(x),Fk(0)=0,k=1,2,…,n*说明：第k步，前后共分配x万元，分配给第k个项目xk；x-xk万元，分配给前k-1个项目；

代码实现如下：

#include <iostream>
#include <vector>

using namespace std;

int main() {

	int m, n;//m元钱，n项投资
	int i, j;
	int tmp_m, tmp_F = 0;
	cout << "请输入投资金额和项目数" << endl;
	cin >> m >> n;
	vector<vector<int>> f(n, vector<int>(m + 1));//f[i][x], 0<i<=n,0<=x<=m；
	vector<vector<int>> F(n, vector<int>(m + 1));//F[i][x]，将x元钱投入到前i个项目上最大的收益
	
	//在第(i+1)个项目上投入0元，收益为0，注意i从0开始
	for (i = 0; i < n; i++) {
		f[i][0] = 0;
	}
	cout << "请输入各项目对应投资金额的收益（从1开始）" << endl;
	for (i = 0; i < n; i++) {
		for (j = 1; j < m + 1; j++) {
			cin >> f[i][j];
		}
	}
	//初始化，给F[0][0-m]赋值
	for (j = 0; j < m + 1; j++) {
		F[0][j] = f[0][j];//第一个项目上投入0-m元钱的最大收益等于f[0][0-m]
	}

	for (i = 1; i < n; i++) {//项目编号，从1开始
		for (j = 0; j < m + 1; j++) {//钱数,从0开始
			for (tmp_m = 0; tmp_m <= j; tmp_m++) {
				//递推公式
				tmp_F = F[i - 1][j - tmp_m] + f[i][tmp_m];
				//取最大值
				if (tmp_F > F[i][j]) {
					F[i][j] = tmp_F;
				}	
			}
		}
	}
	cout << "最大总收益: " << F[n - 1][m] << endl;
}

分析：复杂度 W(n,m)=O(nm2)。

三． 求解完全背包问题

基本原理和思路：1.设置动态规划二维数组dp，dp[i][j]表示从前i个物品中选出重量不超过j（或者剩余容量为j)的物品的最大总价值。
①显然有边界条件：dp[i][0]=0(背包不能装入任何物品时，总价值为0），dp[0][j]=0（没有任何物品可装入时，总价值为0），可以采用memset函数一次性初始化为0.
②另外设置二维数组fk，其中fk[i][j]存放dp[i][j]得到最大值时物品i挑选的件数。

代码实现如下：

//求解完全背包问题的算法
#include <stdio.h>
#include <string.h>
#define MAXN 20				//最多物品数
#define MAXW 100			//最大限制重量
#define max(x,y) ((x)>(y)?(x):(y))
//问题表示
int n,W;
int w[MAXN],v[MAXN];
//求解结果表示
int dp[MAXN+1][MAXW+1],fk[MAXN+1][MAXW+1];
int solve()					//求解多重背包问题
{
	int i,j,k;
	for (i=1;i<=n;i++)
	{
		for (j=0;j<=W;j++)
			for (k=0;k*w[i]<=j;k++)
			{
				if (dp[i][j]<dp[i-1][j-k*w[i]]+k*v[i])
				{
					dp[i][j]=dp[i-1][j-k*w[i]]+k*v[i];
					fk[i][j]=k;		//物品i取k件
				}									
			}
	}
	return dp[n][W];
}
void Traceback()				//回推求最优解
{
	int i=n,j=W;
	while (i>=1)
	{
		printf("物品%d共%d件 ",i,fk[i][j]);
		j-=fk[i][j]*w[i];		//剩余重量
		i--;
	}
	printf("\n");
}
void prin(){   //查看dp数组与fk数组 
	int i,j,k;
	printf("fk[i][j]:\n");
	for (i=1;i<=n;i++)
	{
		for (j=0;j<=W;j++){
			printf("%d ",fk[i][j]);
		}
		printf("\n");
	}
	printf("dp[i][j]:\n");
	for (i=1;i<=n;i++)
	{
		for (j=0;j<=W;j++){
			printf("%d ",dp[i][j]);
		}
		printf("\n");
	}
}
int main()
{
	w[1]=3; w[2]=2; w[3]=6;w[4]=2;
	v[1]=7; v[2]=2; v[3]=5;v[4]=3;
	n=4; W=9;
	memset(dp,0,sizeof(dp));
	memset(fk,0,sizeof(fk));
	printf("最优解:\n");
	printf("  总价值=%d\n",solve());
	printf("  方案: ");Traceback();
	printf("\n");
	prin();
	return 0;
}

img

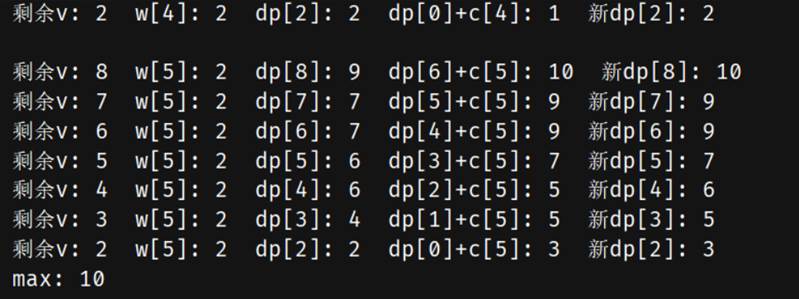
分析：空间复杂度O(nV) 时间复杂度O(nV)。

四．数字三角形

基本原理和思路：MaxSum(i,j)：从第i行j列到底边的最大数字之和
从最后一行开始递推，MaxSum(n,j)=D(n,j)//n行j列，MaxSum(n-1,j) = D(n-1,j) + max( MaxSum(n,j) , MaxSum(n,j+1) )
然后为了减少空间，不需要用二维数组来存储MaxSum(n,j)的值，只需要求MaxSum(n,j)的时候存储下一行MaxSum(n+1,j)的值就可以，然后计算完第n行的MaxSum之后再覆盖原来的第n+1行的MaxSum的值。

代码实现如下：

#include <iostream>
#include <algorithm>
using namespace std;
#define Max 101
int D[Max][Max];
int n;
int maxSum[Max][Max];
int MaxSum(int i,int j)
{
    if(maxSum[i][j]!=-1)
        return maxSum[i][j];
    if(i==n)
        maxSum[i][j]=D[i][j];
    else
    {
        int x=MaxSum(i+1,j);
        int y=MaxSum(i+1,j+1);
        maxSum[i][j]=max(x,y)+D[i][j];
    }
    return maxSum[i][j];
}
int main()
{
    int i,j;
    cin>>n;
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
    {
        cin>>D[i][j];
        maxSum[i][j]=-1;
    }
    cout<<MaxSum(1,1)<<endl;
    return 0;
}

分析：时间复杂度是n2。

五．最小生成树问题

prim算法

基本原理和思路：设G=(V, E)是具有n个顶点的连通网，
T=(U, TE)是G的最小生成树，
T的初始状态为U={u0}（u0∈V），TE={ }，
重复执行下述操作：
在所有u∈U，v∈V-U的边中找一条代价最小的边(u, v)并入集合TE，同时v并入U，直至U=V。
数组lowcost[n]：用来保存集合V-U中各顶点与集合U中顶点最短边的权值，lowcost[v]=0表示顶点v已加入最小生成树中；
数组adjvex[n]：用来保存该边所依附的（集合V-U中各顶点与集合U中顶点的最短边）集合U中的顶点。

代码实现如下：

void prime(MGraph G){
    for(int i=1;i<G.vertexNu;i++){
        lowcost[i]=G.arc[0][i];  adjvex[i]=0;
    }
    lowcost[0]=0;
    for(i=1;i<G.vertexNum;i+++){
        k=MinEdge(lowcost,G.vertexNum)
        cout<<K<<adjvex[k]<<lowcost[k];
        lowcost[k]=0;
        for(j=1;j<G.vertexNum;j++)
          if((G.arc[k][j]<lowcost[j]){
              lowcost[j]=G.arc[k][j];
              arcvex[j]=k;
           }
}

六．背包问题

基本原理和思路：利用动态规划思想 ，子问题为：f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。其状态转移方程是：f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]} //这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只和前i-1件物品相关的问题。
1.如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1; v]；
2.如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为
v-Ci的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值Wi
。

代码实现如下：

int n = 5;
double W = 100;
struct NodeType
{
	double w;
	double v;
	double p;
	bool operator<(const NodeType &s)const
	{
		return p > s.p;
	}
};

NodeType A[] = { {0},{10,20},{20,30},{30,66},{40,40},{50,60} };
double V;
double x[MAXN];

void Knap()
{
	V = 0;
	double weight = W;
	memset(x, 0, sizeof(x));
	int i = 1;

	while (A[i].w < weight)//物品可以全部装入
	{
		x[i] = 1;
		weight -= A[i].w;
		V += A[i].v;
		i++;
	}

	if (weight > 0)//余下物品重量大于0
	{
		x[i] = weight / A[i].w;
		V += x[i] * A[i].v;
	}
}

分析：时间复杂度为O(nlog2n)

实验小结（包括问题和解决方法、心得体会等）

经过这次试验收获颇多，代码实现过程中也遇到一些问题，有的问题确实也有一定的难度，所以也是通过了网络搜索才得出的解决方案，思维上得到了很好的训练，同时也明白了一个道理：纸上得来终觉浅，绝知此事要躬行。尤其是算法和编程这门课程更是要勤于动手方能获得收获。希望下次实验或者之后的编程学习能吸取这些教训。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1599838.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

1.2MHz，固定频率白光LED驱动器

1.2MHz，固定频率白光LED驱动器

一、产品概述 TX6216是一款升压转换器&#xff0c;设计用于通过单节锂离子电池驱动多达7个串联的白光LED。 TX6216采用电流模式&#xff0c;固定频率架构来调节LED电流&#xff0c;LED电流通过外部电流检测电阻测量。其低104mV反馈电压可降低功率损耗并提高效率。 TX6216具有…
阅读更多...
笔试题1 -- 吃掉字符串中相邻的相同字符（点击消除_牛客网）

笔试题1 -- 吃掉字符串中相邻的相同字符（点击消除_牛客网）

吃掉字符串中相邻的相同字符 文章目录 吃掉字符串中相邻的相同字符题目重现解法一&#xff1a;(基于 erase() 函数实现)解法二&#xff1a;&#xff08;利用 栈 辅助实现&#xff09;总结 题目链接&#xff1a; 点击消除_牛客网 题目重现 牛牛拿到了一个字符串。 他每次“点击…
阅读更多...
JMeter控制器数据库获取一组数据后遍历输出

JMeter控制器数据库获取一组数据后遍历输出

目录 1、测试计划中添加Mysql Jar包 2、添加线程组 3、添加 jdbc connection configuration 4、添加JDBC Request&#xff0c;从数据库中获取数据 5.获取数据列表&#xff0c;提取所有goodsName信息 6.通过添加控制器遍历一组数据 6.1 方式一&#xff1a;循环控制器方式 …
阅读更多...
Vue3从入门到实战：深度掌握通信插槽slot

Vue3从入门到实战：深度掌握通信插槽slot

slot_默认插槽的概念&#xff1a; 在Vue中&#xff0c;插槽&#xff08;slot&#xff09;是一种用于在组件中插入内容的特殊技术。默认插槽是其中一种类型的插槽&#xff0c;它允许你在组件的模板中指定一个位置&#xff0c;以便在使用组件时插入自定义的内容。 想象一下你有…
阅读更多...
Linux中安装seata

Linux中安装seata

Linux中安装seata 一、准备1、环境2、下载3、上传到服务器4、解压 二、配置1、备份配置文件2、导入sql3、修改配置前4、修改配置后5、在nacos中配置 三、使用1、启动2、关闭 一、准备 1、环境 因为要在 nacos 中配置&#xff0c;要求安装并启动 nacos 。可以参考这篇博客。 …
阅读更多...
【十一】MyBatis Plus 原理分析

【十一】MyBatis Plus 原理分析

MyBatis Plus 原理分析 摘要 Java EE开发中必不可少ORM框架&#xff0c;目前行业里最流行的orm框架非Mybatis莫属了&#xff0c;而Mybatis框架本身没有提供api实现&#xff0c;所以市面上推出了Mybatis plus系列框架&#xff0c;plus版是mybatis增强工具&#xff0c;用于简化My…
阅读更多...
【JAVA基础篇教学】第十二篇：Java中多线程编程

【JAVA基础篇教学】第十二篇：Java中多线程编程

博主打算从0-1讲解下java基础教学&#xff0c;今天教学第十二篇&#xff1a;Java中多线程编程。 多线程编程是利用多个线程同时执行任务来提高程序的效率和性能。在 Java 中&#xff0c;多线程编程可以通过继承 Thread 类或实现 Runnable 接口来实现。下面是一个简单的多线程…
阅读更多...
IntelliJ IDEA2024 安装包（亲测可用）

IntelliJ IDEA2024 安装包（亲测可用）

目录 一、软件简介 二、软件下载 一、软件简介 IDEA&#xff08;Integrated Development Environment for Apache&#xff09; 是一款专为 Apache 开发者设计的集成开发环境。该软件提供了丰富的功能和工具&#xff0c;帮助开发者更高效地创建、调试和部署 Apache 项目。 主…
阅读更多...
自定义类型: 结构体 (详解)

自定义类型: 结构体 (详解)

本文索引 一. 结构体类型的声明1. 结构体的声明和初始化2. 结构体的特殊声明3. 结构体的自引用 二. 结构体内存对齐1. 对齐规则2. 为啥存在对齐?3. 修改默认对齐值 三. 结构体传参四. 结构体实现位段1. 什么是位段?2. 位段的内存分配3. 位段的应用4. 位段的注意事项 ​ 前言:…
阅读更多...
计算机系列之操作系统的系统

计算机系列之操作系统的系统

2、大话操作系统的启动 当按下开机键时&#xff0c;BIOS 就会开始执行 ​ BIOS 就是放在主板上 ROM 里面的一段程序。 ​ ROM Read Only Memory&#xff08;只能读取的内存&#xff09; ​ 所以 BIOS 在出厂的时候就可以直接写死在 ROM 里面。 ​ 每次开机的时候&#xff…
阅读更多...
JavaScript 高性能编程 —— 加载和运行

JavaScript 高性能编程 —— 加载和运行

JavaScript 在浏览器中的性能，可认为是开发者所要面对的最重要的可用性问题。此问题因 JavaScript 的阻塞特征而复杂，也就是说，当 JavaScript 运行时其他的事情不能被浏览器处理。 事实上，大多数浏览 器使用单进程处理 UI 更新和 JavaScript 运行等多个任务，而同一时间只能…
阅读更多...
Python --- 在python中安装NumPy，SciPy和Matplotlib(Windows平台)

Python --- 在python中安装NumPy，SciPy和Matplotlib(Windows平台)

在python中安装NumPy&#xff0c;SciPy和Matplotlib(Windows平台) NumPy NumPy是Python的一个最常用最基本的扩展程序库之一&#xff0c;主要用于矩阵运算或数组计算。很多其他的python库都要依赖于NumPy才能跑。 NumPy的发展史&#xff1a; Matrix-sig 1995年&#xff0c;特殊…
阅读更多...
设定延迟任务和定时任务并优化定时任务

设定延迟任务和定时任务并优化定时任务

一丶设定延时任务 1.设定延迟任务要求如下 ①在系统中建立easylee用户&#xff0c;设定其密码为easylee ②延迟任务由root用户建立 ③要求在5小时后备份系统中的用户信息文件到/backup中 ④确保延迟任务是使用非交互模式建立 ⑤确保系统中只有root用户和easylee用户可以执…
阅读更多...
【Qt 学习笔记】Qt常用控件 | 按钮类控件Check Box的使用及说明

【Qt 学习笔记】Qt常用控件 | 按钮类控件Check Box的使用及说明

博客主页&#xff1a;Duck Bro 博客主页系列专栏&#xff1a;Qt 专栏关注博主&#xff0c;后期持续更新系列文章如果有错误感谢请大家批评指出&#xff0c;及时修改感谢大家点赞&#x1f44d;收藏⭐评论✍ Qt常用控件 | 按钮类控件Check Box的使用及说明 文章编号&#xff1a;…
阅读更多...
P5730 【深基5.例10】显示屏

P5730 【深基5.例10】显示屏

思路&#xff1a; 此题只需要两层循环&#xff0c;通过数组映射即可求出答案 AC代码&#xff1a; #include<iostream>using namespace std;typedef long long ll; const int N 10; int a[N];int main() {ll n,m;cin >> n >> m;for(ll in;i<m;i){ll nu…
阅读更多...
OpenHarmony实战开发-Worker子线程中解压文件。

OpenHarmony实战开发-Worker子线程中解压文件。

介绍 本示例介绍在Worker 子线程使用ohos.zlib 提供的zlib.decompressfile接口对沙箱目录中的压缩文件进行解压操作&#xff0c;解压成功后将解压路径返回主线程&#xff0c;获取解压文件列表。 效果图预览 使用说明 1.点击解压按钮&#xff0c;解压test.zip文件&#xff0c…
阅读更多...
【JavaSE】你真的了解内部类吗？

【JavaSE】你真的了解内部类吗？

前言 本篇会详细讲解内部类的四种形式&#xff0c;让你掌握内部类~ 欢迎关注个人主页&#xff1a;逸狼 创造不易&#xff0c;可以点点赞吗~ 如有错误&#xff0c;欢迎指出~ 目录 前言 内部类介绍 实例内部类 定义 调用 静态内部类 定义 调用 匿名内部类 定义和调用1 调用方法2 …
阅读更多...
Linux的重要命令（二）+了解Linux目录结构

Linux的重要命令（二）+了解Linux目录结构

目录 一.Linux的目录结构 二.查看文件内容命令 1.cat 命令 2.more 命令 3.less 命令 4.head 命令 5.tail 命令 6.拓展 head 和 tail 的其他用法 ​编辑 三.统计文件内容的命令-wc ​编辑 四.检索和过滤文件内容的命令-grep ​编辑 ​编辑 五.压缩命令 gzip 和 bz…
阅读更多...
碳课堂｜碳关税是什么？企业如何从容应对？

碳课堂｜碳关税是什么？企业如何从容应对？

2023年10月1日&#xff0c;欧盟碳边境调节机制&#xff08;CBAM&#xff09;法规&#xff0c;即全球首个“碳关税”开始实施。据世界银行研究报告称&#xff0c;如果“碳关税”全面实施&#xff0c;在国际市场上&#xff0c;中国制造可能将面临平均26%的关税&#xff0c;出口量…
阅读更多...
【数据结构与算法】之双向链表及其实现！

【数据结构与算法】之双向链表及其实现！

​ 个人主页&#xff1a;秋风起&#xff0c;再归来~ 数据结构与算法 个人格言&#xff1a;悟已往之不谏&#xff0c;知来者犹可追 克心守己&#xff0c;律己则安&#xff01; 目录 1、双向链表的结构及概念 2、双向链表的实现 2.1 要实现的接口…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023