专项1：理论横向误差计算

news2024/11/27 12:29:27

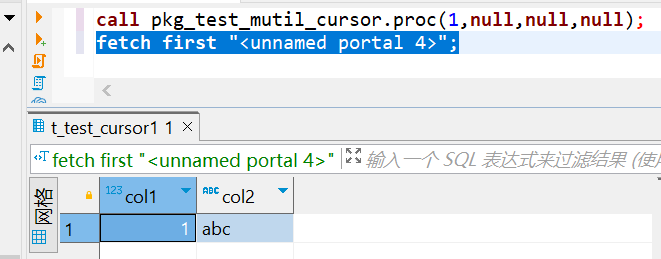
1.前言

车辆实际位置与轨迹要求的位置的误差大小是反映自动驾驶控制精度的关键性指标，也是作为控制系统的输入量。在对车辆的控制算法进行研究时候，首先需要厘清控制系统的输入。控制系统的输入的关键性环节就是笛卡尔坐标系和frent坐标系之间的转换。

2.理论计算时涉及到的物理量

2.1 笛卡尔坐标系与frent坐标系

2.2 专有名词

起始点：参考轨迹的起始点，相对时间戳为0；

匹配点（Xmatch,Ymatch）：根据车辆位置找到参考路径最近点，并以此点建立Frenet坐标系。由位置寻找，与相对时间戳无关；

参考点：根据当前绝对时间戳确定参考点位置；

预瞄点：根据预瞄绝对时间戳确定预瞄点位置，预瞄绝对时间戳=参考绝对时间戳+预瞄时间；

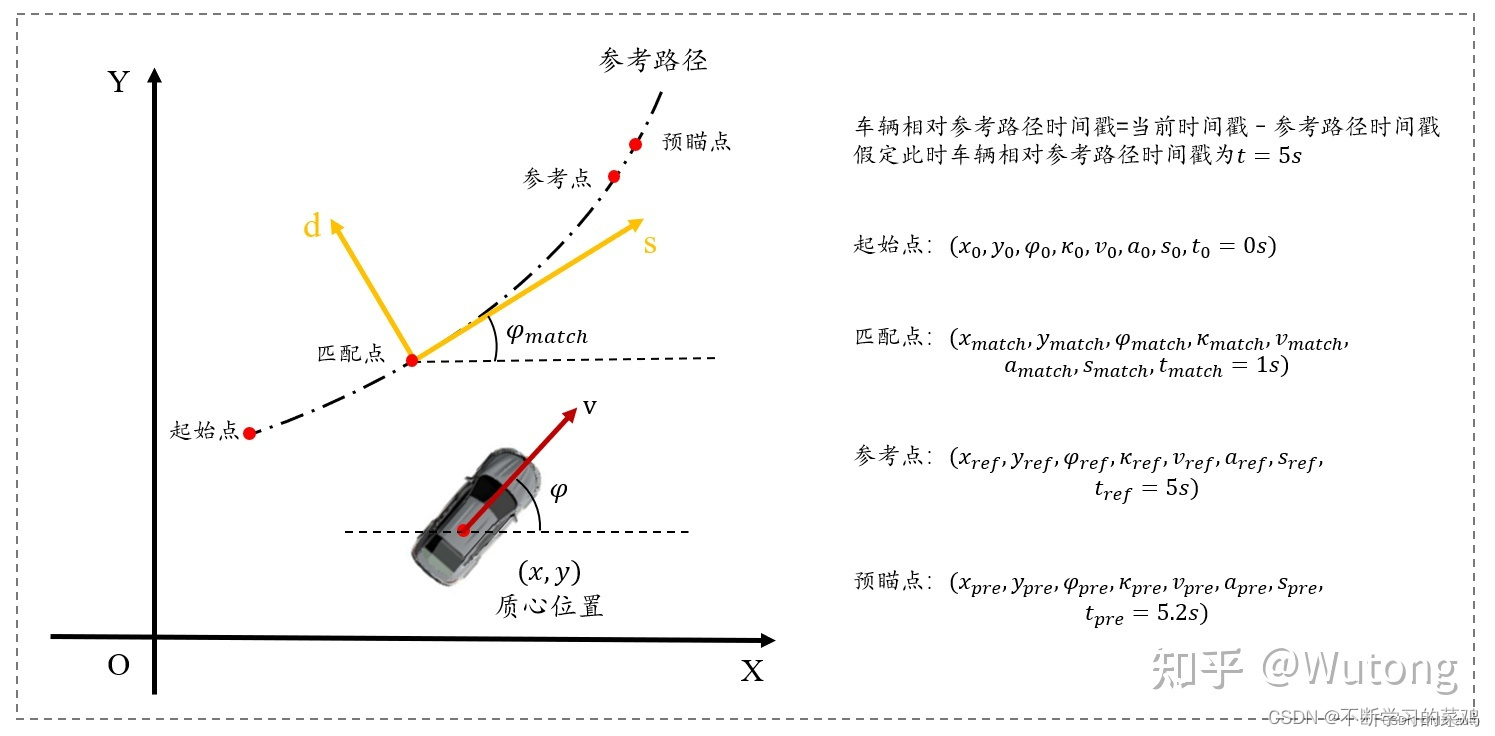
整个问题可以描述为在Cartesian坐标系下，车辆运动状态可以描述为 $\left [ x,y,\theta_{x},v_{x},a_{x},k_{x}\right ]$ ,在frenet坐标系下，车辆的运动状态可以描述为 $\left [ s_{r} ,x_{r},y_{y},\theta _{r},k_{r},{k}'_{r}\right ]$ ，求车辆在Frenet坐标系下的运动状态表达式：

$\left [ s,\dot{s },\ddot{s},d,\dot{d},\ddot{d},{d}',{d}''\right ]$

3.计算方法

在apollo方法中，是以匹配点为原点，建立frent坐标系，然后将笛卡尔坐标系中的（dx,dy）转换到frent坐标系中。

（1）求投影点

Frenet坐标系下的参考线都是由规划模块得到的一系列离散点，假设车辆当前的质心位置矢量为 $\left [ x _{c},y_{c}\right ]$ ,我们找到参考线上距离车辆质心最近的离散点 $\left [ x_{m},y _{m}\right ]$ 作为匹配点，计算匹配点到车辆质心的向量 $\vec{l}$ ,以及匹配点的单位切向量 $\vec{\tau_{m} }$ .

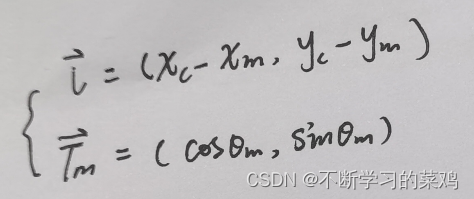
投影点在笛卡尔坐标系下的向量值 $\vec{r}$ 近似等于匹配点的向量值 $\vec{r_{m}}$ 加上向量 $\vec{l}$ 在 $\vec{\tau _{m}}$ 方向上的投影分量，得：

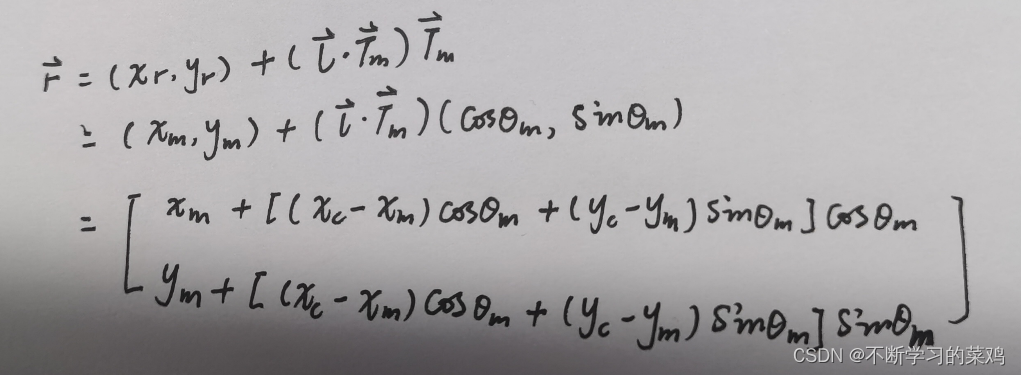
投影点的曲率近似等于匹配点的曲率，即 $k_{r}=k_{m}$ ,而由曲率定义求得投影点

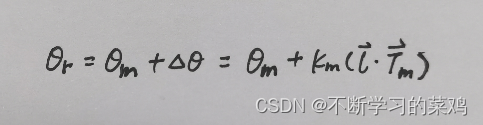
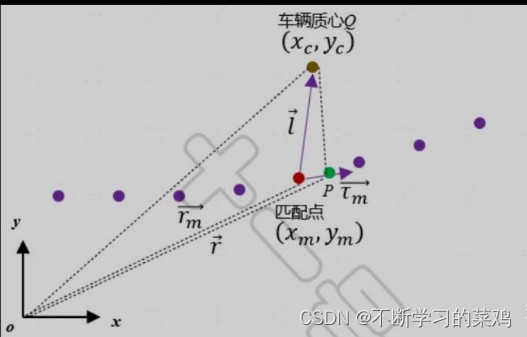
以上就完成了投影点在笛卡尔坐标系下的状态求解，如下图所示，黄色点为车辆质心 $(x_{c},y_{c})$ ,红色点为参考线上的匹配点 $\left ( x_{m}, y_{m}\right )$ ,绿色投影点为 $\left ( x_{r},y_{r}\right )$ .

(2)求s

首先，找到曲线上离位置 $\left ( x,y \right )$ 最近的参考点 $\vec{r}=\left ( x_{r},y_{r} \right )$ （即将位置Q投影到参考线上的投影点P），该参考点处的 $s_{r}$ 就是（x,y）在Frenet坐标系下的s。也可以通过将参考线上的离散点累积求和来得到，但是这种计算会累积误差，只有在局部路径规划中，误差较小且可控。