目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2021年,Zhang等人受到自然界鸭群觅食行为启发,提出了鸭群算法(Duck Swarm Algorithm, DSA)。
2.算法原理
2.1算法思想
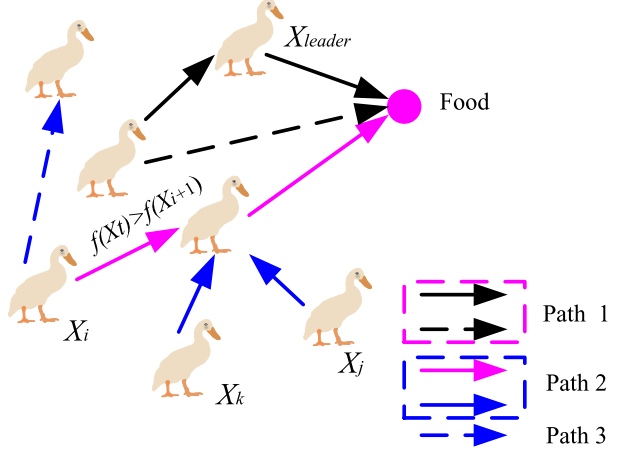
DSA基于自然界鸭群觅食过程,主要分为两个阶段:寻找食物(探索阶段)和群体觅食(开发阶段)。DSA需要遵循两条规则
- 寻找食物时,搜索能力强的鸭子会靠近食物来源的中心,这样会吸引其他个体靠近,更新后的位置也会受到附近个体的影响 (领导者-跟随者类型)
- 觅食时,所有个体都接近食物,下一个位置受到邻近个体和食物位置或领导鸭的影响

2.2算法过程
寻找食物
鸭群逐渐分散并开始寻找食物:
X
i
t
+
1
=
{
X
i
t
+
μ
⋅
X
i
t
⋅
s
i
g
n
(
r
−
0.5
)
,
P
>
r
a
n
d
X
i
t
+
C
F
1
⋅
(
X
l
e
a
d
e
r
t
−
X
i
t
)
+
C
F
2
⋅
(
X
j
t
−
X
i
t
)
,
P
<
r
a
n
d
(1)
\boldsymbol{X}_i^{t+1}=\begin{cases}\boldsymbol{X}_i^t+\mu\cdot\boldsymbol{X}_i^t\cdot sign(r-0.5),P>rand\\\boldsymbol{X}_i^t+CF_1\cdot(\boldsymbol{X}_{leader}^t-\boldsymbol{X}_i^t)+CF_2\cdot(\boldsymbol{X}_j^t-\boldsymbol{X}_i^t),P<rand\end{cases}\tag{1}
Xit+1={Xit+μ⋅Xit⋅sign(r−0.5),P>randXit+CF1⋅(Xleadert−Xit)+CF2⋅(Xjt−Xit),P<rand(1)
其中,sign函数表示对寻找食物的方向。整体来看(1)式可以看作个体周围扰动(P>rand),领域个体和最优个体引导(P<rand),平衡因子为:
μ
=
K
⋅
(
1
−
t
/
t
max
)
K
=
sin
(
2
⋅
r
a
n
d
)
+
1
(2)
\mu=K\cdot(1-t / t_{\max} )\\K=\sin(2\cdot rand )+1\tag{2}
μ=K⋅(1−t/tmax)K=sin(2⋅rand)+1(2)
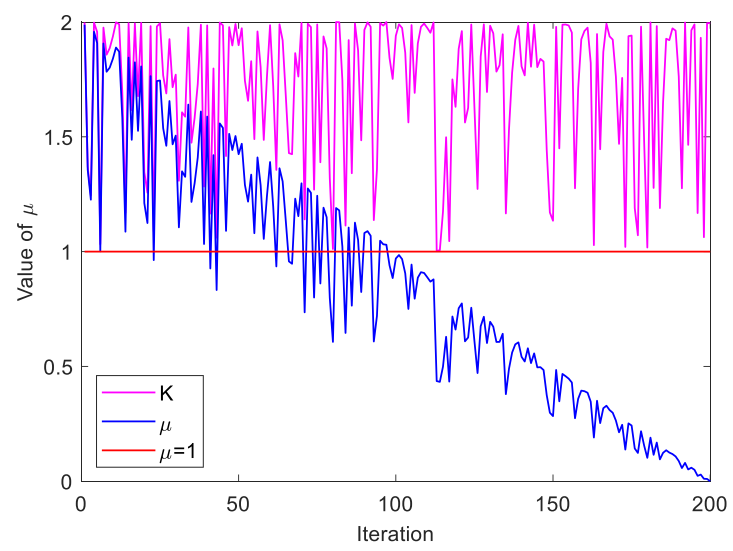
平衡因子通过参数K控制,整体呈线性递减。PS:这里可以改进为非线性因子
群体觅食
鸭群寻找食物后,即有足够的食物可以满足鸭群的觅食:
X
i
t
+
1
=
{
X
i
t
+
μ
⋅
(
X
l
e
a
d
e
r
t
−
X
i
t
)
,
f
(
X
i
t
)
>
f
(
X
i
t
+
1
)
X
i
t
+
K
F
1
⋅
(
X
l
e
a
d
e
r
t
−
X
i
t
)
+
K
F
2
⋅
(
X
k
t
−
X
j
t
)
,
e
l
s
e
(3)
\boldsymbol{X}_i^{t+1}=\begin{cases}\boldsymbol{X}_i^t+\mu\cdot(\boldsymbol{X}_{leader}^t-\boldsymbol{X}_i^t),f(X_i^t)>f(X_i^{t+1})\\\boldsymbol{X}_i^t+KF_1\cdot(\boldsymbol{X}_{leader}^t-\boldsymbol{X}_i^t)+KF_2\cdot(\boldsymbol{X}_k^t-\boldsymbol{X}_j^t),else\end{cases}\tag{3}
Xit+1={Xit+μ⋅(Xleadert−Xit),f(Xit)>f(Xit+1)Xit+KF1⋅(Xleadert−Xit)+KF2⋅(Xkt−Xjt),else(3)
参数可以表述为:
C
F
i
o
r
K
F
i
←
1
F
P
⋅
r
a
n
d
(
0
,
1
)
(
i
=
1
,
2
)
(4)
CF_i\mathrm{~or~}KF_i\leftarrow\frac1{FP}\cdot rand(0,1)(i=1,2)\tag{4}
CFi or KFi←FP1⋅rand(0,1)(i=1,2)(4)
其中,FP为常数0.618。
伪代码

3.结果展示
使用测试框架,测试DSA性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
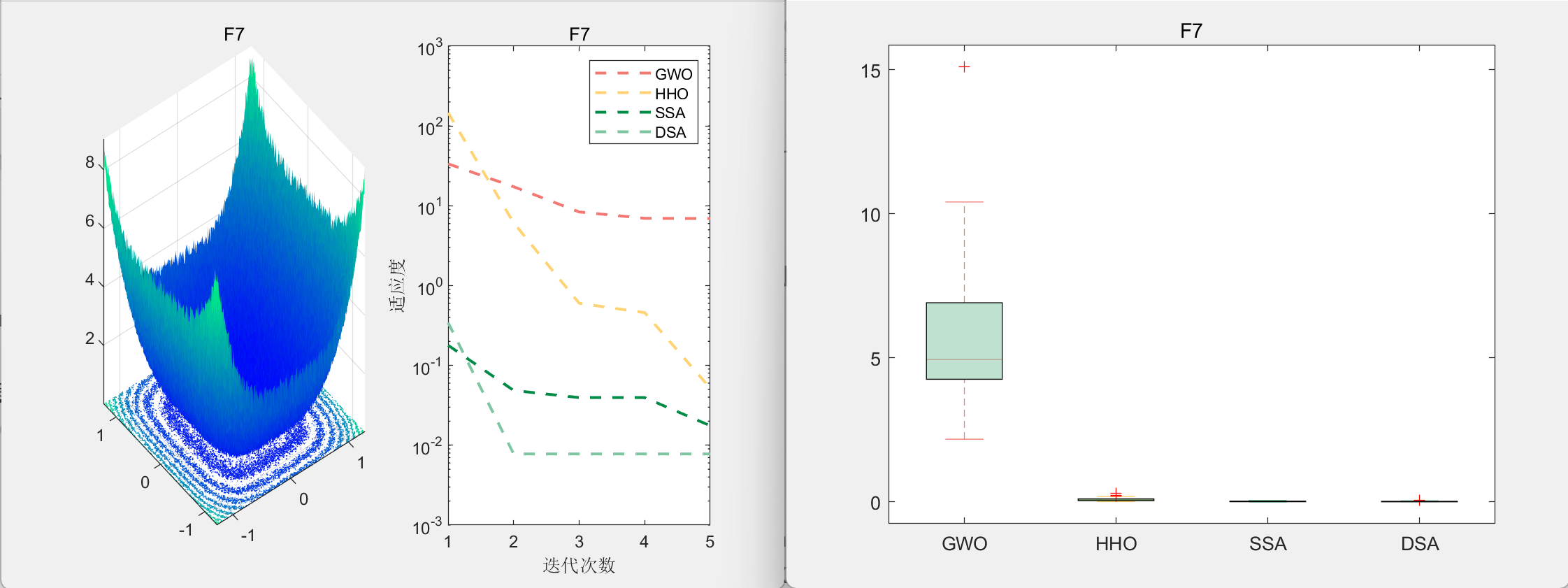
CEC2005-F7
Frieddamn检验
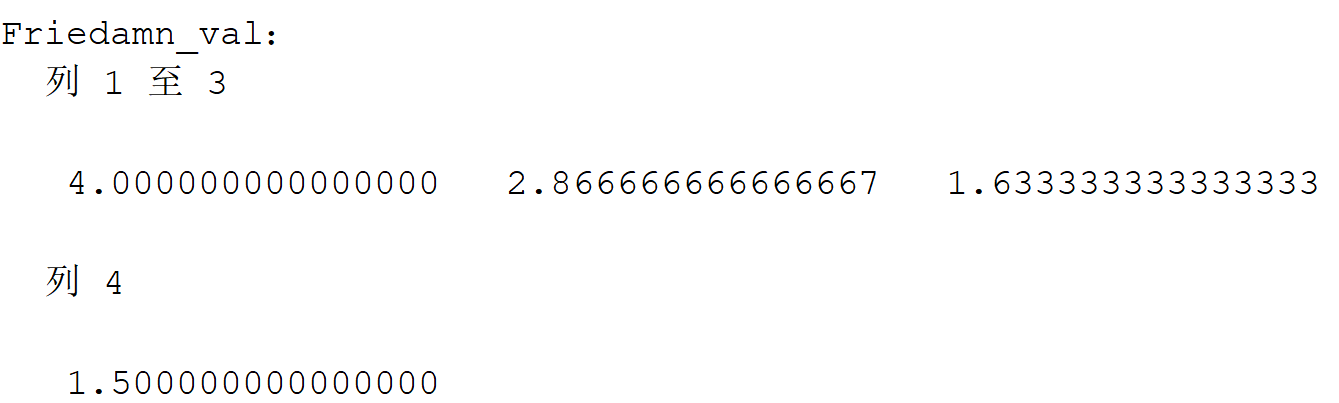
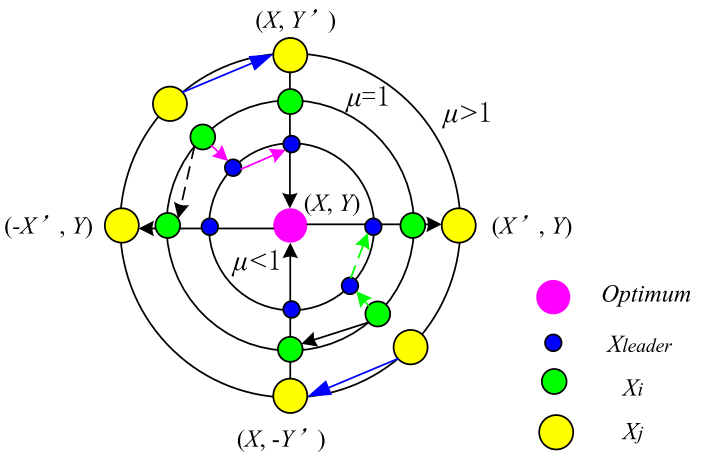
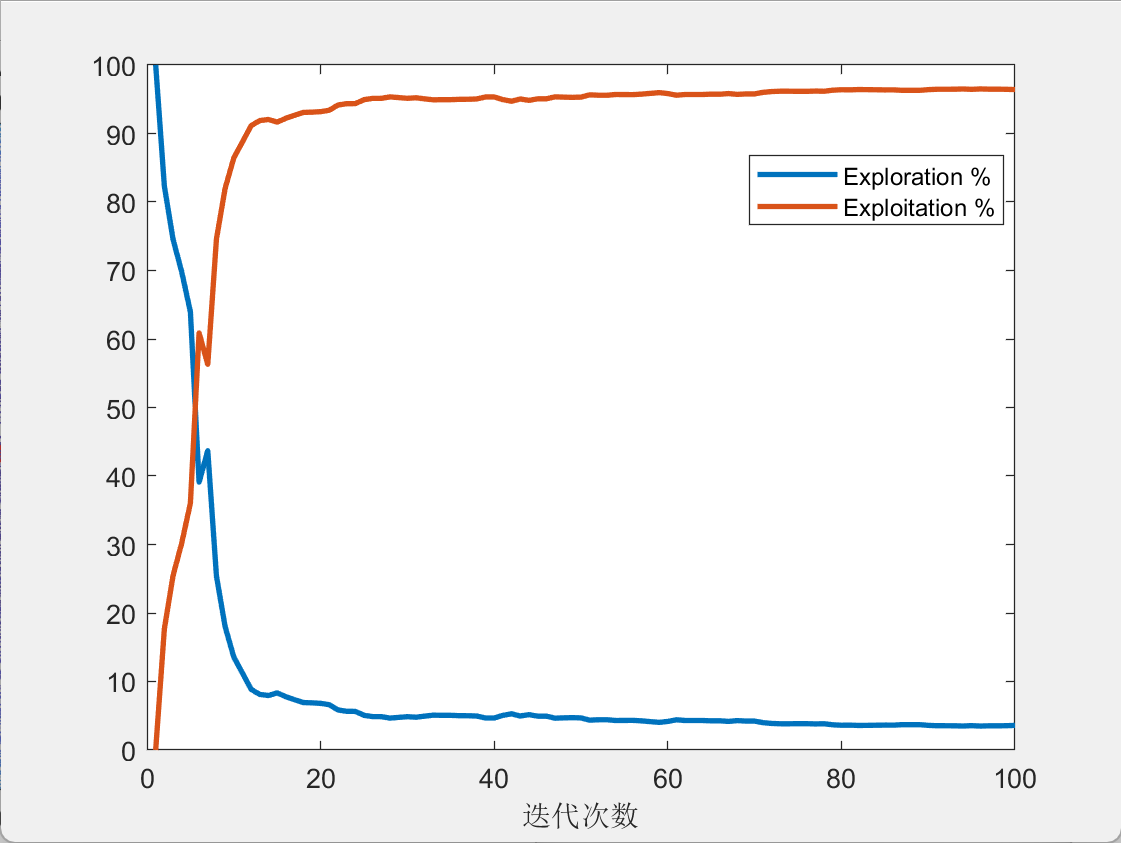
探索与开发
种群空间搜索图

4.参考文献
[1] Zhang M, Wen G, Yang J. Duck swarm algorithm: A novel swarm intelligence algorithm. arXiv 2021[J]. arXiv preprint arXiv:2112.13508.